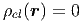

Im Vakuum gibt es keine Teilchen, also auch keine geladenen Teilchen. Wir können also setzen:
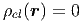
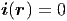
Damit lauten die Maxwellgleichungen [?] in der Integralform
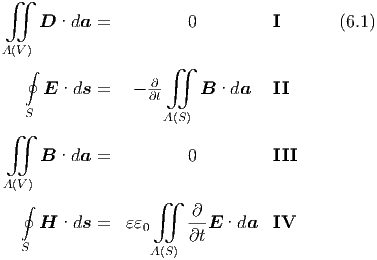
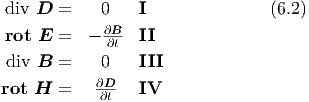
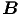 = μ0
= μ0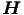 sowie
sowie 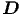 = 𝜀0
= 𝜀0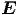 sowie μ = 1
und 𝜀 = 1. Zur Ableitung der Wellengleichung sind die
differentiellen Maxwellgleichungen besser als die integralen
geeignet. Wir verwenden μ0𝜀0 = 1∕c2 und erhalten also
Die Maxwellgleichungen im Vakuum sind symmetrisch
bezüglich
sowie μ = 1
und 𝜀 = 1. Zur Ableitung der Wellengleichung sind die
differentiellen Maxwellgleichungen besser als die integralen
geeignet. Wir verwenden μ0𝜀0 = 1∕c2 und erhalten also
Die Maxwellgleichungen im Vakuum sind symmetrisch
bezüglich 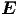 und
und 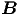 . Wir nehmen die Rotation der zweiten
Maxwellgleichung.
. Wir nehmen die Rotation der zweiten
Maxwellgleichung.
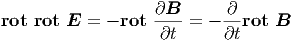 | (6.4) |
Indem wir die Austauschbarkeit von Ableitungen verwenden.
Nun setzt man die vierte Maxwellgleichung in die zweite
Gleichung ein. Wir erhalten eine Differentialgleichung für 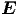 allein.
allein.
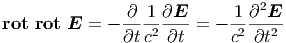 | (6.5) |
Nun gilt die Vektoridentität
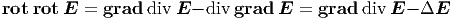 | (6.6) |
Wegen der ersten Maxwellgleichung verschwindet der erste Term auf der rechten Seite. Also lauten die Wellengleichungen
|
sowie nach einer analogen Ableitung für 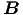
|
Die nicht-trivialen Lösungen der Wellengleichungen heissen elektromagnetische Wellen. Dieses Phänomen ist implizit in den Maxwellgleichungen enthalten, die aus makroskopischen Experimenten abgeleitet wurden. Die Wellengleichung beschreibt alle Wellenphänomene aus der Kommunikationstechnik, der Optik und der Wechselwirkung von Atomen und Molekülen untereinander, für Abstände von 1nm oder mehr. Die Maxwellgleichungen sind invariant unter der Lorentz-Transformation, nicht aber unter der Galilei-Transformation. In jedem Inertialsystem im Vakuum ist die Ausbreitungsgeschwindigkeit
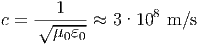 | (6.9) |
Damit haben die Maxwellgleichungen implizit schon 1864 die spezielle Relativitätstheorie vorweggenommen.
In Medien ist die Ausbreitungsgeschwindigkeit entsprechend
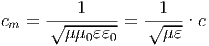 | (6.10) |
wobei μ die relative Permeabilität und 𝜀 die relative Permittivität ist.
 Lizenzinformationen
Lizenzinformationen