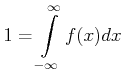Weiter: Varianzen und Standardabweichungen
Oben: Statistische Fehler
Zurück: Stichproben
Aus diesem Histogramm kann man den Mittelwert
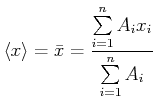 |
(3.2) |
berechnen. Hier sind die 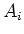 die Häufigkeiten der in eine bestimmte Klasse fallenden Messwerte. In unserem Falle
(Siehe Abbildung 3.1) ist dies
die Häufigkeiten der in eine bestimmte Klasse fallenden Messwerte. In unserem Falle
(Siehe Abbildung 3.1) ist dies
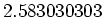 . Man kann diese Gleichung umschreiben, indem man die
relativen Häufigkeiten
. Man kann diese Gleichung umschreiben, indem man die
relativen Häufigkeiten
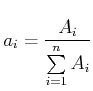 |
(3.3) |
verwendet. Der Mittelwert ist dann
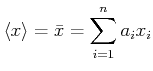 |
(3.4) |
Der so gefundene Mittelwert ist im allgemeinen nicht mit dem wahren Wert der Messgrösse identisch.
Wenn wir die Klassenbreite verringern und gleichzeitig die Anzahl Messpunkte erhöhen, so erhält man die
differentielle Verteilungsfunktion 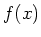 der zugrunde liegenden Gesamtheit. Diese Funktion
der zugrunde liegenden Gesamtheit. Diese Funktion 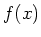 ist normiert,
da wir die relativen Häufigkeiten zu ihrer Ableitung verwendet hatten.
ist normiert,
da wir die relativen Häufigkeiten zu ihrer Ableitung verwendet hatten.
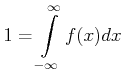 |
(3.5) |
Wir müssen unterscheiden zwischen den aus den experimentellen Daten empirisch gefundenen Verteilungsfunktionen und
den durch theoretische Modelle berechneten Verteilungen. Eine wichtige Aufgabe einer Datenanalyse kann sein, zu
zeigen, dass eine empirische Verteilungsfunktion mit einer theoretisch gefundenen verträglich ist.





Next: Varianzen und Standardabweichungen
Up: Statistische Fehler
Previous: Stichproben
Othmar Marti
Experimentelle Physik
Universiät Ulm
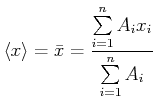
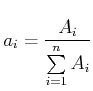
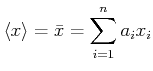
![]() der zugrunde liegenden Gesamtheit. Diese Funktion
der zugrunde liegenden Gesamtheit. Diese Funktion ![]() ist normiert,
da wir die relativen Häufigkeiten zu ihrer Ableitung verwendet hatten.
ist normiert,
da wir die relativen Häufigkeiten zu ihrer Ableitung verwendet hatten.