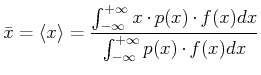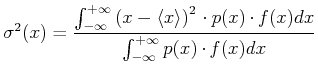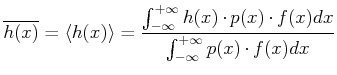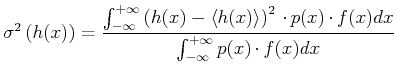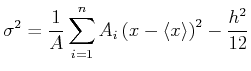Weiter: Mittlerer Fehler und Varianz
Oben: Statistische Fehler
Zurück: Mittelwerte
Eine Verteilungsfunktion ist nicht nur durch ihren Mittelwert, sondern auch durch die Lage-und Dispersionsgrössen
gegeben. Wir haben gesehen, dass der arithmetische Mittelwerte(Mittelwerteoben) eine solche Grösse ist. Die
Lagegrössen müssen die folgenden Postulate erfüllen:
- Die Schätzung soll im Falle einer unendlich grossen Stichprobe den Wert der Grundgesamtheit annehmen.
- Die beste Schätzung ist die mit der kleinsten Streuung, d.h. mit der kleinsten Fehlerabweichung.
Als Lagegrössen kommen in Frage:
Der Median ist besonders dann zu verwenden, wenn die Stichprobe eine grosse Streuung aufweist. Wenn aus anderen
Daten bekannt ist, dass nicht alle Messwerte die gleiche Güte haben, kann man die A; auch als Gewicht benutzen.
Hier hatten wir die Anzahl Messwerte pro Klasse als Güte des Messwertes genommen.
Es ist einsichtig, dass man zusätzlich versucht, die Breite einer Verteilung zu charakterisieren. Diese Grössen
heissen Dispersionsgrössen. Man verwendet:
- Den durchschnittlichen Fehler:
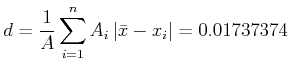 |
(3.8) |
- Die Varianz:
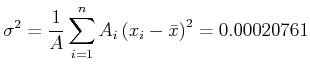 |
(3.9) |
Wenn man die Varianz bezüglich eines anderen Wertes 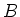 bildet, so gilt mit
bildet, so gilt mit
die Gleichung
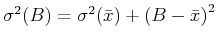 |
(3.11) |
Da dies alles positiv definite Grössen sind, ist die Varianz minimal, wenn sie bezüglich des arithmetischen
Mittelwertes 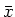 berechnet wird.
berechnet wird.
Wenn wir eine kontinuierliche Verteilung 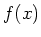 haben und
haben und 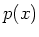 die Gewichtsfunktion ist, gilt:
die Gewichtsfunktion ist, gilt:
- Arithmetischer Mittelwert:
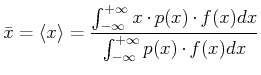 |
(3.12) |
- Varianz:
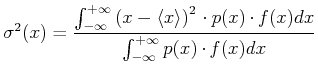 |
(3.13) |
- allgemein gilt: Der mit der Verteilungsfunktion
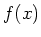 und
Gewichtsfunktion
und
Gewichtsfunktion 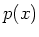 bewertete Mittelwert der Funktion
bewertete Mittelwert der Funktion 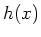 ist
ist
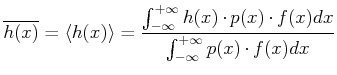 |
(3.14) |
- Die Varianz der Funktion
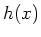 ist
ist
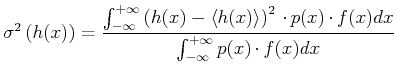 |
(3.15) |
Shepard gibt an, dass ein besserer Wert für die Varianz erhalten
wird bei in Klassen eingeteilten Messgrössen, wenn man die
folgende Formel verwendet.
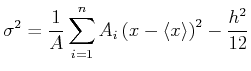 |
(3.16) |
wobei 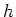 die Klassenbreite ist. In unserem Falle wäre
die Klassenbreite ist. In unserem Falle wäre
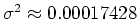 .
.





Next: Mittlerer Fehler und Varianz
Up: Statistische Fehler
Previous: Mittelwerte
Othmar Marti
Experimentelle Physik
Universiät Ulm
![$\displaystyle G(x)=\sqrt[A]{\prod\limits_{i=1}^{n}x_i^{a_i}}=2.58292652$](img22.gif)
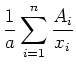
![$\displaystyle G(x)=\sqrt[A]{\prod\limits_{i=1}^{n}x_i^{a_i}}=2.58292652$](img22.gif)
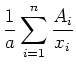
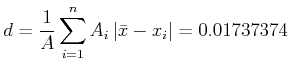
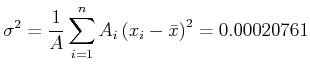
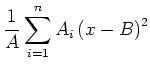
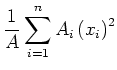
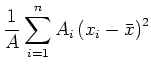
![]() haben und
haben und ![]() die Gewichtsfunktion ist, gilt:
die Gewichtsfunktion ist, gilt: