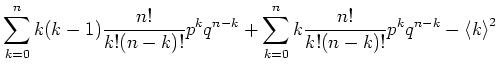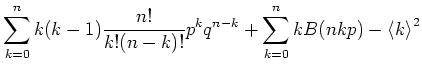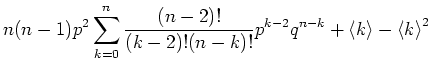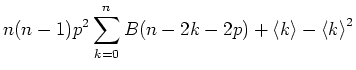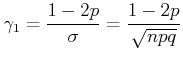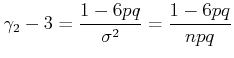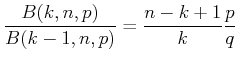Weiter: Normalverteilung
Oben: Verteilungen
Zurück: Verteilungen
Die Binomialverteilung beschreibt Experimente, bei denen in jedem einzelnen Experiment mit der Wahrscheinlichkeit
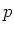 ein Ereignis eintritt und mit der Wahrscheinlichkeit
ein Ereignis eintritt und mit der Wahrscheinlichkeit 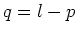 ein zweites Ereignis eintritt (oder das erste
nicht eintritt). Zum Beispiel genügt ein Würfelspiel diesen Gesetzen. Die Wahrscheinlichkeit, dass
ein zweites Ereignis eintritt (oder das erste
nicht eintritt). Zum Beispiel genügt ein Würfelspiel diesen Gesetzen. Die Wahrscheinlichkeit, dass 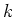 -mal das
erste und
-mal das
erste und 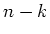 mal das zweite Ereignis innerhalb von insgesamt
mal das zweite Ereignis innerhalb von insgesamt 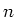 Ereignissen eintritt ist
Ereignissen eintritt ist
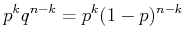 |
(5.36) |
Wenn die Reihenfolge dieser Ereignisse irrelevant ist, dann hat man die Binomialverteilung
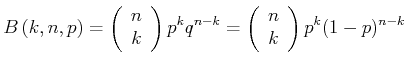 |
(5.37) |
Die Verteilung ist normiert, da gilt
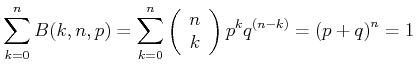 |
(5.38) |
Der Mittelwert ist
Die Varianz schliesslich berechnet sich zu
Die weiteren Momente sind (ohne Rechnung)
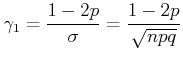 |
(5.42) |
und
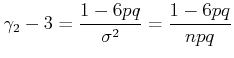 |
(5.43) |
Für die Binomialverteilung existiert eine Rekursionsformel:
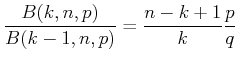 |
(5.44) |
Zum Abschluss noch eine kurze Bemerkung: jede, auch asymmetrische Binomialverteilung geht für festes 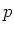 bei
grossen
bei
grossen
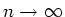 in die Normalverteilung über.
in die Normalverteilung über.





Next: Normalverteilung
Up: Verteilungen
Previous: Verteilungen
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() ein Ereignis eintritt und mit der Wahrscheinlichkeit
ein Ereignis eintritt und mit der Wahrscheinlichkeit ![]() ein zweites Ereignis eintritt (oder das erste
nicht eintritt). Zum Beispiel genügt ein Würfelspiel diesen Gesetzen. Die Wahrscheinlichkeit, dass
ein zweites Ereignis eintritt (oder das erste
nicht eintritt). Zum Beispiel genügt ein Würfelspiel diesen Gesetzen. Die Wahrscheinlichkeit, dass ![]() -mal das
erste und
-mal das
erste und ![]() mal das zweite Ereignis innerhalb von insgesamt
mal das zweite Ereignis innerhalb von insgesamt ![]() Ereignissen eintritt ist
Ereignissen eintritt ist
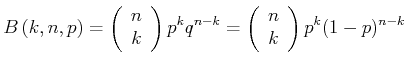
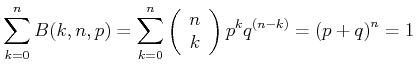
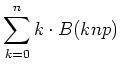
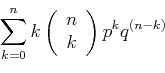
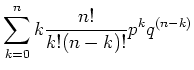
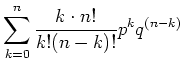
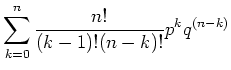
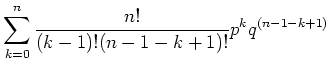
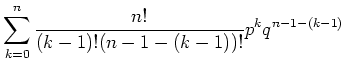
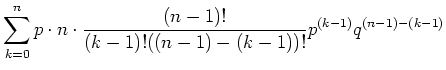
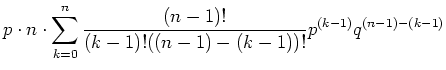
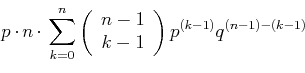
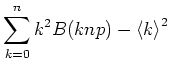
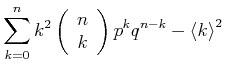
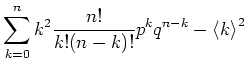
![$\displaystyle \sum\limits_{k=0}^n \left[k(k-1)+k\right] \frac{n!}{k!(n-k)!}p^kq^{n-k}-\left< k \right>^2$](img131.gif)