



Weiter: Poisson-Verteilung
Oben: Verteilungen
Zurück: Binomialverteilung
Die Normalverteilung kann als Grenzfall der Binomialverteilung angesehen werden, wenn die Anzahl Versuche gegen
unendlich geht und 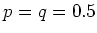 ist. Die Wahrscheinlichkeit für das Auftreten einer Abweichung ist
ist. Die Wahrscheinlichkeit für das Auftreten einer Abweichung ist
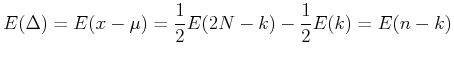 |
(5.45) |
wobei 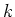 negative und
negative und 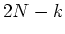 positive Abweichungen auftreten. Wir können die Binomialverteilung verwenden:
positive Abweichungen auftreten. Wir können die Binomialverteilung verwenden:
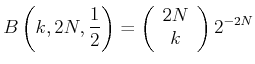 |
(5.46) |
Wir berechnen den Mittelwert. Mit
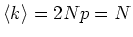 wird
wird
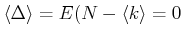 |
(5.47) |
oder
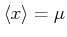 |
(5.48) |
Die Varianz wird dann
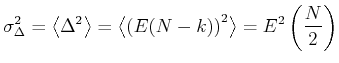 |
(5.49) |
Für grosse 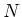 ist es sinnvoll, die Verteilung auf die Varianz
ist es sinnvoll, die Verteilung auf die Varianz 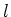 zu standardisieren
zu standardisieren
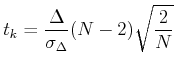 |
(5.50) |
Diese standardisierte Variable 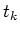 hat den Mittelwert 0 und die Varianz
hat den Mittelwert 0 und die Varianz 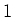 . Verwenden nun Histogramme, und
skalieren die Achse mit
. Verwenden nun Histogramme, und
skalieren die Achse mit
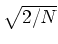 erhalten wir
erhalten wir
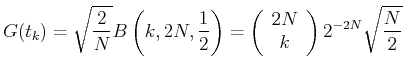 |
(5.51) |
Mit der Stirlingschen Formel
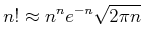 |
(5.52) |
wird
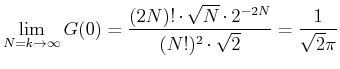 |
(5.53) |
Mit Hilfe der Rekursionsformel kann gezeigt werden, dass
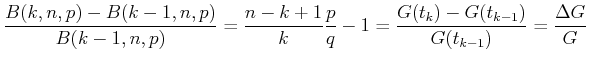 |
(5.54) |
Für 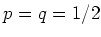 wird
wird
Für
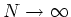 ergibt sich
ergibt sich
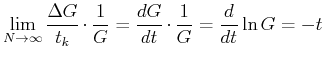 |
(5.56) |
Daraus folgt
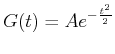 |
(5.57) |
Mit einer Normierung erhält man die standardisierte Gaussverteilung
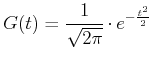 |
(5.58) |
oder die allgemeine Gaussverteilung
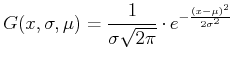 |
(5.59) |
Die Gaussverteilung ist symmetrisch bezüglich des Mittelwertes 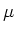 , also sind alle ungradzahligen Momente den
Wert 0. Die gradzahligen Momente haben den Wert
, also sind alle ungradzahligen Momente den
Wert 0. Die gradzahligen Momente haben den Wert
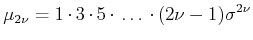 |
(5.60) |
Damit wird zum Beispiel die Überhöhung
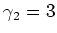 .
.
Viele Experimente ergeben eine gaussförmige Verteilung der Messwerte um einen Mittelwert. Zur Abschätzung von
Fehlergrenzen kann das Integral der Gaussverteilung, die Fehlerfunktion verwendet
werden.
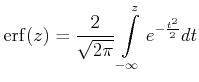 |
(5.61) |
Für den speziellen Wert
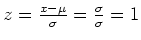 wird
wird
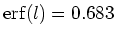 . Das heisst: bei normalverteilten
statistischen Abweichungen ist die Wahrscheinlichkeit
. Das heisst: bei normalverteilten
statistischen Abweichungen ist die Wahrscheinlichkeit 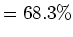 , dass eine Messung einen Fehler innerhalb
, dass eine Messung einen Fehler innerhalb
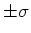 liefert.
liefert.




Next: Poisson-Verteilung
Up: Verteilungen
Previous: Binomialverteilung
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() ist. Die Wahrscheinlichkeit für das Auftreten einer Abweichung ist
ist. Die Wahrscheinlichkeit für das Auftreten einer Abweichung ist
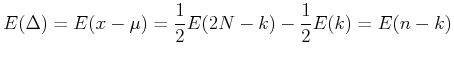
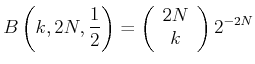
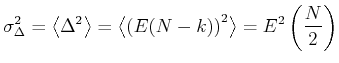
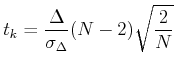
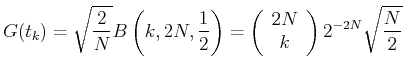
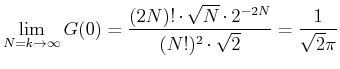
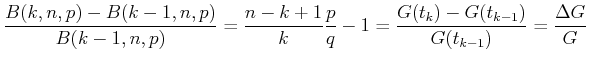
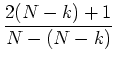
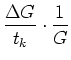
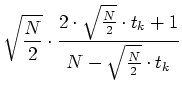
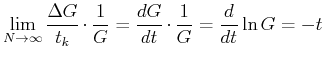
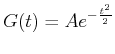
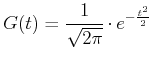
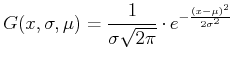
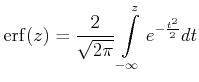
![]() wird
wird
![]() . Das heisst: bei normalverteilten
statistischen Abweichungen ist die Wahrscheinlichkeit
. Das heisst: bei normalverteilten
statistischen Abweichungen ist die Wahrscheinlichkeit ![]() , dass eine Messung einen Fehler innerhalb
, dass eine Messung einen Fehler innerhalb
![]() liefert.
liefert.