




Weiter: Bibliographie
Oben: Ausgleichsrechnung ''Fitten''
Zurück: Numerische Verfahren
Die Anpassung von empirisch gefundenen oder theoretisch begründeten funktionalen Zusammenhängen an gemessene Daten
ist nicht in jedem Falle einfach. Bei lineare Zusammenhängen funktionieren die meisten Programme sehr gut. Bei
nichtlinearen Abhängigkeiten, die insbesondere über mehrere Grössenordnungen betrachtet werden müssen, sind
meistens Probleme zu befürchten.
Die Datenanpassung beruht auf den im obigen Kapitel angegebenen Verfahren, unter Umständen auch auf wesentlich
involvierteren Verfahren wie sie in den Referenzen [Grä81] und [Bev69] beschrieben werden. Weitere Texte finden Sie im Internet wenn Sie nach "Fehlerrechnung" suchen.
In diesem Teil der Vorlesung sollen Sie mit den Möglichkeiten einer Tabellenkalkulation für diese Anpassungen
vertraut gemacht werden. Natürlich können auch andere Programmpakete, oft sogar besser, als Excel, das hier als
Beispiel genommen wird, verwendet werden. Excel ist jedoch unschlagbar, wenn es um das Antasten an ein
Anpassungsverfahren geht.
Als Beispiel verwende ich 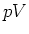 -Daten des Gases
-Daten des Gases 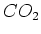 . Diese Daten wurden mit einem sich im Aufbau befindlichen
Experiment des Grundpraktikums gemessen. Das Experiment läuft so ab, dass mit einer Mikrometerschraube das
Probenvolumen, ausgehend von einem unbekannten Volumen
. Diese Daten wurden mit einem sich im Aufbau befindlichen
Experiment des Grundpraktikums gemessen. Das Experiment läuft so ab, dass mit einer Mikrometerschraube das
Probenvolumen, ausgehend von einem unbekannten Volumen 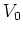 verändert wird. Eine weitere Unbekannte ist die
Molzahl
verändert wird. Eine weitere Unbekannte ist die
Molzahl 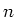 , da diese nur schlecht zu bestimmen ist.
, da diese nur schlecht zu bestimmen ist.
Wir starten mit einem leeren Bildschirm.
|
In diesen Bildschirm tragen wir nun oben den Titel ein
|
Es ist eine gute Praxis, die relevanten Gleichungen im Seitenkopf anzugeben. Hier enthalten die Zellen B4
und B5 die Umrechnungsgleichungen von den gemessenen Daten auf die physikalischen Grössen.
In der Zelle B8 geben wir die Gleichung des realen Gases ein, in der Zelle B9 die
Auflösung nach 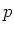 . .
|
|
Wir geben nun in den Zellen A12 und A13 die Bezeichnungen der unbekannten Grössen ein.
Die Zellen B12 und B13 enthalten Anfangswerte, die Zellen C12 und C13 die physikalischen
Einheiten.
|
|
Die Zellen F3 bis I11 enthalten die Literaturwerte.
|
|
Wir markieren nun den Bereich G4 bis Hll. Mit dem Befehl Einfügen - Namen -
Erstellen... werden die Bezeichnungen der Namen festgelegt.
|
|
Wir wählen nun die Funktion aus linker Spalte aus.
|
Damit werden die Namen erzeugt, die dann als absolute Referenz in Formeln verwendet werden.
In die Zelle B16 wird die Temperatur des Gases eingegeben. Beachten Sie, dass mit absoluten Temperaturen
gerechnet werden muss. Die Umrechnung kann, wie hier gezeigt, direkt in Excel durchgeführt werden.
|
Als nächstes geben wir die Messwerte ein, für die Mikrometerschraube in mm und für den Druck in mV. Dies
sind die Einheiten, die wir ablesen. Es ist eine schlechte Praxis, schon vor dem Notieren der Werte Umrechnungen
durchzuführen. Wenn bei diesen Umrechnungen nämlich ein Fehler passiert, dann ist er nicht mehr auszumerzen, Wenn
die Umrechnungen erst im nachhinein geschehen, haben solche Fehler, wenn sie entdeckt werden, keine Konsequenz.
|
Als nächstes berechnen wir in der Spalte C die Volumenverringerung. Die Formel ist abgeleitet aus
der in Zelle B4. Dabei wird zuerst das Volumen 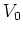 ausser Acht gelassen, also nur ausser Acht gelassen, also nur
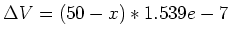 ausgerechnet. ausgerechnet.
|
|
Wir markieren nun den Bereich, in den die Formel kopiert werden sollte. Mit Strg-U füllen wir den
Bereich.
|
In der Spalte D wird nun das Volumen ausgerechnet. In der Formel
=$B$12-C19 bedeutet die
Zellenreferenz $B$12 das Volumen 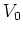 . $B bedeutet, dass
beim Kopieren sich diese Spaltenreferenz nicht verändern sollte. $12 bedeutet, dass die Zeilenreferenz
beim Kopieren nicht verändert werden soll. $B$12 bedeutet also eine
absolute Referenz. C19 sagt, dass beim kopieren die Zellenreferenz
relativ aufzufassen ist. Man kann auch Kombinationen verwenden, bei der nur die Spalten oder nur die Zeilen
absolute Referenzen sind. . $B bedeutet, dass
beim Kopieren sich diese Spaltenreferenz nicht verändern sollte. $12 bedeutet, dass die Zeilenreferenz
beim Kopieren nicht verändert werden soll. $B$12 bedeutet also eine
absolute Referenz. C19 sagt, dass beim kopieren die Zellenreferenz
relativ aufzufassen ist. Man kann auch Kombinationen verwenden, bei der nur die Spalten oder nur die Zeilen
absolute Referenzen sind.
|
|
Die Spalte E enthält den in Pascal umgerechneten Druck. Dabei wird die in der Zelle B5
angegebene Umrechnung verwendet.
|
In der Spalte F wird nun der Druck mit der van der Waals Gas-Theorie ausgerechnet.
$B$13 ist die zu berechnende Molzahl, D19 das Volumen, das implizit das Volumen 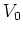 enthält. enthält.
|
|
Die Spalte G enthält nun die Berechnung des Fehlers. Hier verwenden wir das Fehlerquadrat. In der
Zelle B14 wird nun die Summe aller Fehler eingetragen.
|
Nun können von Hand die freien Parameter verändert werden.
Das erlaubt einem, den realistischen Parameterbereich abzuschätzen.
|
Zur automatischen Abschätzung benötigen wir den Solver.
|
Die Einstellungen sehen wie oben aus.
Die Zielzelle enthält die Referenz auf die Zelle, die minimiert werden soll. Der Solver funktioniert besser, wenn
nicht nach einem Minimum, das ja auch lokal sein kann, sondern nach dem Zielwert 0 gesucht wird. Veränderbare
Zellen sind die Molzahl und das Volumen 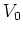 . Die Nebenbedingungen verhindern, dass bei der Suche durch 0 geteilt
wird. Unter den Optionen kann der Suchalgorithmus bestimmt werden. . Die Nebenbedingungen verhindern, dass bei der Suche durch 0 geteilt
wird. Unter den Optionen kann der Suchalgorithmus bestimmt werden.
|
Nach dem Starten des Lösungsprozesses läuft die Suche. Ist sie fündig geworden, wird der folgende Dialog
angezeigt. Wir sagen OK und unsere Datei sieht nun wie oben aus.
Beachten Sie die Zielzelle, und die beiden
veränderbaren Zellen. Sie zeigen nun das Resultat des Fits.
|
|
Es hilft oft, sich eine graphische Darstellung des Fits anzusehen. Dazu markieren wir die Spalte mit dem
Volumen sowie die beiden Druckspalten.
|
|
Wir drücken nun auf den Knopf für den Diagrammassistenten. Nun wählen wir Ein Liniendiagramm ohne
Datenpunkte aus und drücken Weiter.
|
|
Wir erhalten eine Vorschau. Wir beschriften im nächsten Dialog das Diagramm und fügen es als neue Seite
ein.
|
|
Sie sehen, dass der Fit nicht sehr gut ist.
|
Ein Grund ist das 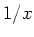 -Verhalten der Kurve. Wir gleichen die Steigungen in den unterschiedlichen
Bereichen an, indem wir die zu fittende Gleichung logarithmieren. -Verhalten der Kurve. Wir gleichen die Steigungen in den unterschiedlichen
Bereichen an, indem wir die zu fittende Gleichung logarithmieren.
|
Nun ritten wir wieder und erhalten
| V0 |
4,67852E-06 |
m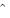 3 3 |
| n= |
0,000633095 |
mol |
| |
Summe Abweichung |
1,558E+00 |
|
Resultat des Fits mit einer logarithmischen Gleichung.
|
Spielen Sie mit der beiliegenden Datei Aprechnung.xls. Sie enthält die oben gezeigten Rechnungen.





Next: Bibliographie
Up: Ausgleichsrechnung ''Fitten''
Previous: Numerische Verfahren
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() -Daten des Gases
-Daten des Gases ![]() . Diese Daten wurden mit einem sich im Aufbau befindlichen
Experiment des Grundpraktikums gemessen. Das Experiment läuft so ab, dass mit einer Mikrometerschraube das
Probenvolumen, ausgehend von einem unbekannten Volumen
. Diese Daten wurden mit einem sich im Aufbau befindlichen
Experiment des Grundpraktikums gemessen. Das Experiment läuft so ab, dass mit einer Mikrometerschraube das
Probenvolumen, ausgehend von einem unbekannten Volumen ![]() verändert wird. Eine weitere Unbekannte ist die
Molzahl
verändert wird. Eine weitere Unbekannte ist die
Molzahl ![]() , da diese nur schlecht zu bestimmen ist.
, da diese nur schlecht zu bestimmen ist.
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig169.eps}](img423.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig170.eps}](img424.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig171.eps}](img425.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig172.eps}](img426.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig173.eps}](img427.gif)
![\includegraphics[width=0.6\textwidth]{fehlerrechnung_2003Fig174.eps}](img428.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig175.eps}](img429.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig176.eps}](img430.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig177.eps}](img432.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig178.eps}](img433.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig179.eps}](img434.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig180.eps}](img435.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig181.eps}](img436.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig182.eps}](img437.gif)
![\includegraphics[width=0.8\textwidth]{fehlerrechnung_2003Fig183.eps}](img438.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig184.eps}](img439.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig185.eps}](img440.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig186.eps}](img441.gif)
![\includegraphics[width=0.7\textwidth]{fehlerrechnung_2003Fig187.eps}](img442.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig188.eps}](img443.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig189.eps}](img444.gif)
![\includegraphics[width=\textwidth]{fehlerrechnung_2003Fig190.eps}](img447.gif)