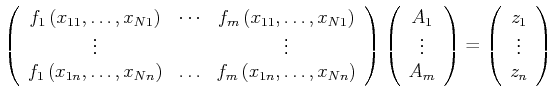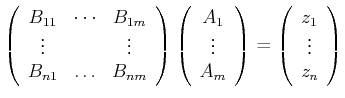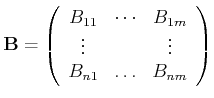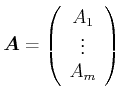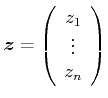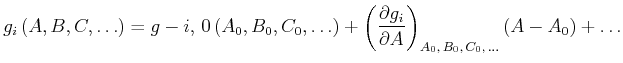



Weiter: Verwenden von Excel zum
Oben: Ausgleichsrechnung ''Fitten''
Zurück: Graphische Verfahren
Unterabschnitte
Wir betrachten nun zuerst den einfachen Fall einer linearen Beziehung zwischen zwei Grössen. Bei einer Feder wären
dies die Auslenkung 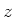 , die angewandte Kraft
, die angewandte Kraft 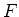 und die Lage des Nullpunktes
und die Lage des Nullpunktes 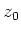 . Ohne Verlust der
Allgemeinheit kann
. Ohne Verlust der
Allgemeinheit kann 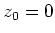 gesetzt werden. Folgende Annahmen können nun gemacht werden:
gesetzt werden. Folgende Annahmen können nun gemacht werden:
- Die Messung der Kraft F ist fehlerbehaftet
- Die Messung der Position z ist fehlerbehaftet
- Beide Messgrössen sind fehlerbehaftet.
In diesem Falle können wir den Fehler für den 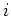 -ten Messpunkt wie folgt angeben:
-ten Messpunkt wie folgt angeben:
Das Prinzip der kleinsten Fehlerquadrate verlangt nun , dass
![$\displaystyle \sum\limits_{i=1}^n \epsilon_i^2 = \left[\epsilon\;\epsilon\right]=\textrm{minimal}$](img371.gif) |
(8.103) |
ist.
![$\left[\epsilon\;\epsilon\right]$](img372.gif) ist eine Abkürzung für die Summe.
Also
ist eine Abkürzung für die Summe.
Also
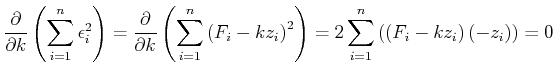 |
(8.104) |
Diese Gleichung kann umgeschrieben werden:
![$\displaystyle 0 = k\sum\limits_{i=1}^n z_i^2 -\sum\limits_{i=1}^n F_i z_i = k\left[z\; z\right]-\left[F\; z\right]$](img374.gif) |
(8.105) |
oder
![$\displaystyle k = \frac{\left[F\; z\right]}{\left[z\; z\right]}$](img375.gif) |
(8.106) |
Wir können die Gleichung für den Zusammenhang zwischen der Auslenkung und der Kraft auch so umschreiben, dass 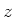 unsicher ist. Dann gilt
unsicher ist. Dann gilt
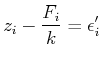 |
(8.107) |
Eine kurze Rechnung zeigt, dass in diesem Falle
![$\displaystyle k = \frac{\left[F\; F\right]}{\left[F\; z\right]}$](img377.gif) |
(8.108) |
ist.
Wenn beide Messgrössen fehlerbehaftet sind, gilt:
Abstand von Messpunkt und Ausgleichsgerade, wenn beide Messwerte fehlerbehaftet sind. Hier ist 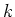 ein
Schätzwert für die Federkonstante. ein
Schätzwert für die Federkonstante. |
Anhand der Zeichnung 8.2.3 findet man heraus, dass
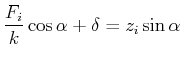 |
(8.109) |
oder
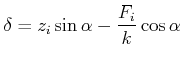 |
(8.110) |
Die Summe der Abstandsquadrate muss null sein, also muss
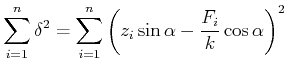 |
(8.111) |
minimal sein. Also ist
Also wird
Nun ist aber
![$\displaystyle k' = \tan\alpha = \tan\left(\frac{\arctan\left(\frac{2\left[z\;\f...
...{\left[z\;z\right]-\left[\frac{F_i}{k}\;\frac{F_i}{k}\right]}\right)}{2}\right)$](img392.gif) |
(8.114) |
Die wahre Federkonstante ist dann
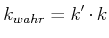 |
(8.115) |
wobei 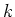 der ursprüngliche Schätzwert der Federkonstante war.
der ursprüngliche Schätzwert der Federkonstante war.
|
Als Beispiel ist in dieser Figur eine mit Zufallszahlen simulierte Rechnung zu sehen. |
In der Abbildung 8.2.3 bedeuten fkz die angepasste Kurve, wenn nur 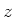 fehlerbehaftet ist,
fkf, die Anpassung, bei der
fehlerbehaftet ist,
fkf, die Anpassung, bei der 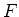 einen Fehler hat sowie fkfz die Anpassung, bei der beide Grössen
einen Fehler haben. Bei der letzten Kurve wurde die besprochene quadratische Anpassung durchgeführt. Wichtig ist,
dass dafür ein Schätzwert der Federkonstante k verwendet wurde.
einen Fehler hat sowie fkfz die Anpassung, bei der beide Grössen
einen Fehler haben. Bei der letzten Kurve wurde die besprochene quadratische Anpassung durchgeführt. Wichtig ist,
dass dafür ein Schätzwert der Federkonstante k verwendet wurde.
Wir betrachten nun die allgemeine Beziehung
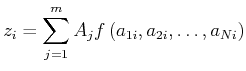 |
(8.116) |
bei der die unbekannten Koeffizienten 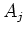 linear in den Gleichungen vorkommen. Wir fordern wieder, dass
linear in den Gleichungen vorkommen. Wir fordern wieder, dass
![$\displaystyle \left[\epsilon\;\epsilon\right] = \sum\limits_{i=1}^n \epsilon_i^...
...n A_j f\left(a_{1i},a_{2i},\ldots,a_{Ni}\right)-z_i \right\}^2=\textrm{Minimum}$](img397.gif) |
(8.117) |
ist. Die Gleichung kann auch in Matrixschreibweise geschrieben werden:
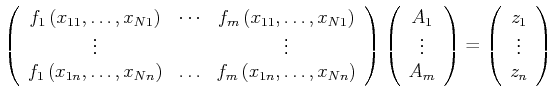 |
(8.118) |
Mit der Abkürzung
wird die Gleichung
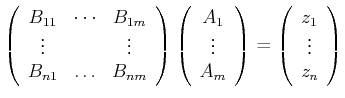 |
(8.119) |
oder
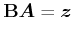 |
(8.120) |
wobei
und
ist. Die Lösung dieses überbestimmten GleichungsSystems im Sinne der Minimierung der Fehlerquadrate ist die Lösung
des
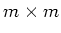 -Gleichungssystems
-Gleichungssystems
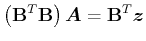 |
(8.121) |
also
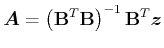 |
(8.122) |
Bei allgemeinen funktionalen Abhängigkeiten sucht man, mit welcher Methode auch immer, Näherungswerte für die
unbekannten Parameter. Ist zum Beispiel
und 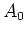 ,
,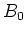 ,
,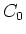 ,
,  Näherungswerte der Parameter, so kann eine Taylor-Entwicklung durchgeführt werden.
Näherungswerte der Parameter, so kann eine Taylor-Entwicklung durchgeführt werden.
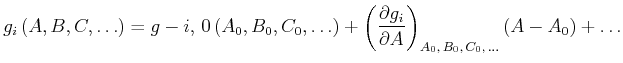 |
(8.123) |
Mit
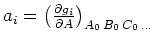 ,
,
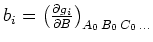 ,
, 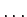 ,
,
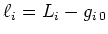 und
und
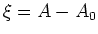 ,
,
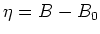
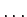 ist die Gleichung wieder in linearisierter Form vorhanden.
ist die Gleichung wieder in linearisierter Form vorhanden.
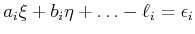 |
(8.124) |
Die oben skizzierte Methode kann zur Lösung beliebiger Anpassunmgsprobleme in der Nähe von Punkten verwendet
werden, bei denen eine Linearisierung möglich ist. Weiter Informationen können im Buch von Zurmühl [Zur63]
gefunden werden.




Next: Verwenden von Excel zum
Up: Ausgleichsrechnung ''Fitten''
Previous: Graphische Verfahren
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() , die angewandte Kraft
, die angewandte Kraft ![]() und die Lage des Nullpunktes
und die Lage des Nullpunktes ![]() . Ohne Verlust der
Allgemeinheit kann
. Ohne Verlust der
Allgemeinheit kann ![]() gesetzt werden. Folgende Annahmen können nun gemacht werden:
gesetzt werden. Folgende Annahmen können nun gemacht werden:
![]() -ten Messpunkt wie folgt angeben:
-ten Messpunkt wie folgt angeben:
![$\displaystyle \sum\limits_{i=1}^n \epsilon_i^2 = \left[\epsilon\;\epsilon\right]=\textrm{minimal}$](img371.gif)
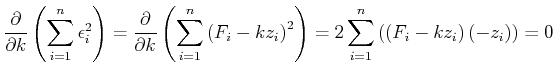
![$\displaystyle 0 = k\sum\limits_{i=1}^n z_i^2 -\sum\limits_{i=1}^n F_i z_i = k\left[z\; z\right]-\left[F\; z\right]$](img374.gif)
![$\displaystyle k = \frac{\left[F\; z\right]}{\left[z\; z\right]}$](img375.gif)
![]() unsicher ist. Dann gilt
unsicher ist. Dann gilt
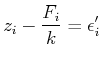
![$\displaystyle k = \frac{\left[F\; F\right]}{\left[F\; z\right]}$](img377.gif)
![\includegraphics[width=0.95\textwidth]{fehlerrechnung_2003Fig148.eps}](img378.gif)
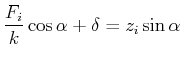
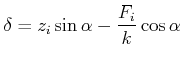
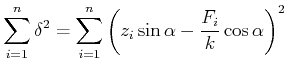
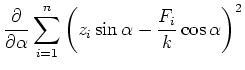
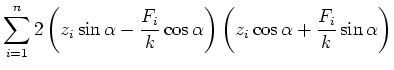
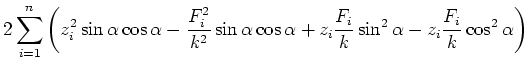
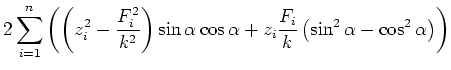
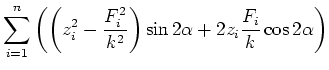
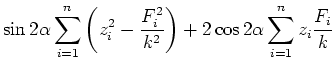
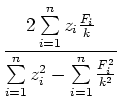
![$\displaystyle \frac{2\left[z\;\frac{F_i}{k}\right]}{\left[z\;z\right]-\left[\frac{F_i}{k}\;\frac{F_i}{k}\right]}$](img391.gif)
![$\displaystyle k' = \tan\alpha = \tan\left(\frac{\arctan\left(\frac{2\left[z\;\f...
...{\left[z\;z\right]-\left[\frac{F_i}{k}\;\frac{F_i}{k}\right]}\right)}{2}\right)$](img392.gif)
![\includegraphics[width=0.9\textwidth]{fehlerrechnung_2003Fig152.eps}](img394.gif)
![]() fehlerbehaftet ist,
fkf, die Anpassung, bei der
fehlerbehaftet ist,
fkf, die Anpassung, bei der ![]() einen Fehler hat sowie fkfz die Anpassung, bei der beide Grössen
einen Fehler haben. Bei der letzten Kurve wurde die besprochene quadratische Anpassung durchgeführt. Wichtig ist,
dass dafür ein Schätzwert der Federkonstante k verwendet wurde.
einen Fehler hat sowie fkfz die Anpassung, bei der beide Grössen
einen Fehler haben. Bei der letzten Kurve wurde die besprochene quadratische Anpassung durchgeführt. Wichtig ist,
dass dafür ein Schätzwert der Federkonstante k verwendet wurde.
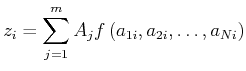
![$\displaystyle \left[\epsilon\;\epsilon\right] = \sum\limits_{i=1}^n \epsilon_i^...
...n A_j f\left(a_{1i},a_{2i},\ldots,a_{Ni}\right)-z_i \right\}^2=\textrm{Minimum}$](img397.gif)