Weiter: Mechanik starrer Körper Oben: Relativität Zurück: Klassische Relativität beschleunigter Bezugssysteme Skript: PDF-Datei Übungen: Blätter
![\includegraphics[width=0.8\textwidth]{relativ-013}](img1450.gif)
|
Jeder Schwimmer habe die Geschwindigkeit ![]() gegen das Wasser, beide schwimmen die Strecke
gegen das Wasser, beide schwimmen die Strecke ![]() hin und zurück
hin und zurück
Schwimmer 1) schwimmt vom Pfeiler zur Boje und zurück.
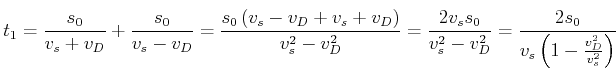
Schwimmer 2) schwimmt vom Pfeiler ans Ufer und zurück. Damit er wieder beim Pfeiler ankommt, muss er seine
Schwimmrichtung um den Winkel ![]() gegen die Strömung vorhalten.
gegen die Strömung vorhalten.
![\includegraphics[width=0.2\textwidth]{relativ-014}](img1454.gif)
Vorhalten des Schwimmers 2.
|
Der Vorhaltewinkel wird gegeben durch
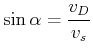 |
(4.421) |
| (4.422) |
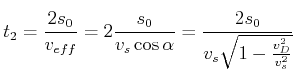 |
(4.423) |
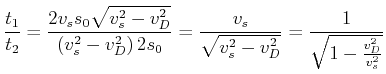 |
(4.424) |
unabhängig von ![]() .
.
Der Zeitunterschied ist, andererseits
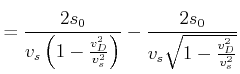 |
||
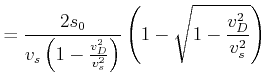 |
||
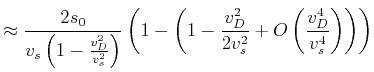 |
||
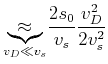 |
||
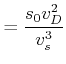 |
(4.425) |
Wir machen nun die folgende Identifikation
Wir erhalten also
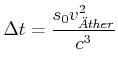 |
(4.426) |
![\includegraphics[width=0.4\textwidth]{relativ-016}](img1471.gif)
Michelson-Morley-Experiment: Interferometrische Längenmessung.
|
Der zu ![]() gehörende Weglängenunterschied
gehörende Weglängenunterschied ![]() ist
ist
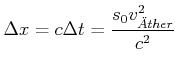 |
(4.427) |
Im Michelson-Morley-Versuch erwartet man für die verwendeten Parameter
![\begin{displaymath}
\left.
\begin{array}[c]{c}
L=10m\\
\lambda=300nm\\
v_{\d...
...ght\} \text{eine Verschiebung um knapp einen Interferenzring.}
\end{displaymath}](img1474.gif)
Wenn man eine Verschiebung um einen Viertel Interferenzring
beobachten kann, dann gilt für die Äthergeschwindigkeit
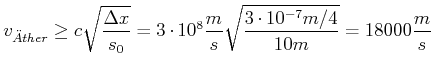 |
(4.428) |
Wie die Rechnung zeigt, ist das Michelson-Morley-Experiment an der Grenze der Signifikanz. Der aufgrund der Messdaten durchaus zweifelhafte Befund der beiden wurde später glänzend bestätigt. Heute wird eine äquivalente Technik zur Gravitationswellendetektion angewandt.
Es wurde aber kein Gangunterschied beobachtet über eine Jahreszeit. Es gibt nun zwei Lösungen:
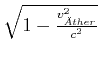 kürzer wird und so die Laufzeit kompensiert. Experimente mit
elektrischen Ladungen zeigen diese Längenkontraktion
kürzer wird und so die Laufzeit kompensiert. Experimente mit
elektrischen Ladungen zeigen diese Längenkontraktion
Das Experiment kann so interpretiert werden: Das Interferometer bewegt sich gleich schnell gegenüber dem Äther, unabhängig von der Position auf der Erdbahn.
(Siehe Tipler, Physik [Tip94, pp. 1156]) (Siehe Gerthsen, Physik [Mes04, pp. 838])
|
Eine andere Formulierung des 2. Postulates ist
|
Jeder Beobachter misst für die Lichtgeschwindigkeit |
Anders kann man auch sagen
(Siehe Gerthsen, Physik [Mes04, pp. 838])
Ereignisse sind durch einen Ort und eine Zeit gegeben. Dies kann so ausgedrückt werden, dass 4 Koordinaten zur Angabe eines Ereignisses notwendig sind.
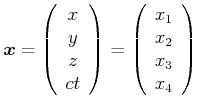 |
(4.429) |
Wir multiplizieren hier die Zeit mit der Lichtgeschwindigkeit, um ihr die Einheit einer Länge zu geben.
| Zwei Ereignisse sind in jedem Inertialsystem gleichzeitig, wenn sie am Ort und zur gleiche Zeit (an dem betreffenden Ort) stattfinden. |
| Ein Bezugssystem ist allgemein formuliert ein System von Mechanismen und materiellen Körpern, (Z.B. Uhren und Massstäbe), mit deren Hilfe die Lage anderer Körper zu einem bestimmten Zeitpunkt relativ zu den Massstäben angegeben werden kann (das Punktereignis). |
| Ein Körper ist also eine Folge von Punktereignissen. Man nennt diese Linie die Weltlinie des Körpers. |
All das was sich auf mich wirkt, oder auf was ich wirken kann, muss sich in einem Gebiet befinden, von dem aus ein
Punktereignis mit dem jetzt mit einer Geschwindigkeit ![]() verbunden werden kann. In einem
Koordinatensystem mit den Achsen
verbunden werden kann. In einem
Koordinatensystem mit den Achsen ![]() ,
, ![]() ,
, ![]() und
und ![]() bedeutet dies, dass nur Punktereignisse
aufeinander einwirken können, bei denen die Steigung der Verbindungslinie steiler als
bedeutet dies, dass nur Punktereignisse
aufeinander einwirken können, bei denen die Steigung der Verbindungslinie steiler als ![]() ist.
ist.
(Siehe Gerthsen, Physik [Mes04, pp. 839])
![\includegraphics[width=0.4\textwidth]{relativ-017}](img1482.gif)
Rückdatierung der Beobachtung eines Ereignisses auf die wahre Zeit und den wahren Ort.
|
Wenn ich weiss, dass die Nachricht von einem Ereignis mich mit einer bestimmten Laufzeit aus einer bestimmten Richtung erreicht, kann ich die Zeit und den Ort des Ereignisses bestimmen. Durch diese sogenannte Rückdatierung kann es mir gelingen, festzustellen, wann und wo ein oder mehrere Ereignisse stattgefunden haben sowie ob mehrere Ereignisse für andere Beobachter gleichzeitig sind.
| Um die Lage eines Punktereignisses in einer für alle möglichen Beobachter nachvollziehbaren Weise anzugeben, muss das Hilfsmittel der Rückdatierung angewandt werden. |
Im Regelfall werden bei der Diskussion der speziellen Relativitätstheorie Licht- oder Radiosignale verwendet. Sie
haben den Vorteil, dass ihre Ausbreitungsgeschwindigkeit in allen Inertialsystemen ![]() ist. Natürlich könnten wir
auch Schall, oder jedes andere Medium verwenden: die Berechnungen wären durch die niedrigere
Geschwindigkeit bedingt aber komplizierter.
ist. Natürlich könnten wir
auch Schall, oder jedes andere Medium verwenden: die Berechnungen wären durch die niedrigere
Geschwindigkeit bedingt aber komplizierter.
![\includegraphics[width=0.5\textwidth]{relativ-018}](img1483.gif)
Die Zeitachse wird mit
|
Wir definieren als Mass (verallgemeinerte Längenmessung)
| (4.430) |
Dies ist analog zum Euklidischen Mass
![\includegraphics[width=0.7\textwidth]{relativ-019}](img1490.gif)
Die zwei Novae sollen an den angegebenen Orten und Zeiten ausbrechen. B
befindet sich in einem Inertialsystem, das sich mit der Geschwindigkeit
|
In der Abbildung stellt die horizontale Achse alle drei Raumkoordinaten zusammen dar. Am Ort ![]() befindet sich A in Ruhe. Deshalb ist die Zeitachse von A sein hier. Andererseits haben alle Punkte auf
der
befindet sich A in Ruhe. Deshalb ist die Zeitachse von A sein hier. Andererseits haben alle Punkte auf
der ![]() -Achse die gleich Zeit wie A, sie befinden sich also jetzt. Die hier und
jetzt eines sich in einem mit der Geschwindigkeit
-Achse die gleich Zeit wie A, sie befinden sich also jetzt. Die hier und
jetzt eines sich in einem mit der Geschwindigkeit ![]() gegenüber A's Inertialsystem bewegenden
Beobachters B sind gekippt gegenüber meinen Koordinatenachsen, wobei der Kippwinkel
gegenüber A's Inertialsystem bewegenden
Beobachters B sind gekippt gegenüber meinen Koordinatenachsen, wobei der Kippwinkel ![]() der Zeitachse (
der Zeitachse (![]() ,
hier) durch die Geschwindigkeit gegeben ist. Unbekannt ist der Kippwinkel
,
hier) durch die Geschwindigkeit gegeben ist. Unbekannt ist der Kippwinkel ![]() der Raumachse (
der Raumachse (![]() ,
jetzt). B soll gleichzeitig die Explosion von je einer Nova links und rechts von ihm beobachten. Beide
Novae sollen den gleichen Abstand von B haben. Sie sollen, als B's Weltlinie die von A kreuzte ausgebrochen sein
,
jetzt). B soll gleichzeitig die Explosion von je einer Nova links und rechts von ihm beobachten. Beide
Novae sollen den gleichen Abstand von B haben. Sie sollen, als B's Weltlinie die von A kreuzte ausgebrochen sein
Dies kann wie folgt eingesehen werden:
Zwischenbeobachtung: Die beiden roten Linien unter ![]() stellen die Ausbreitung des Lichtes dar, die
Lichtgeraden: die Lichtgeschwindigkeit bei unserer Wahl der Koordinaten ist 1. Die beiden
roten Linien durch die beiden Ereignisse zeigen, dass B beide Novae gleichzeitig wahrnimmt. A hingegen sieht
zuerst die Nova 1, dann die Nova 2, da der Schnittpunkt der ersten roten Linie mit der
stellen die Ausbreitung des Lichtes dar, die
Lichtgeraden: die Lichtgeschwindigkeit bei unserer Wahl der Koordinaten ist 1. Die beiden
roten Linien durch die beiden Ereignisse zeigen, dass B beide Novae gleichzeitig wahrnimmt. A hingegen sieht
zuerst die Nova 1, dann die Nova 2, da der Schnittpunkt der ersten roten Linie mit der ![]() -Achse unter dem der
zweiten Linie liegt.
-Achse unter dem der
zweiten Linie liegt.
| Der Begriff der Gleichzeitigkeit hängt vom betrachteten Inertialsystem ab. |
| (4.431) |
| Diagramme wie das aus der Abbildung 4.18 heissen Minkowski-Diagramme. |
Je schneller ![]() ist, desto mehr werden, von
ist, desto mehr werden, von ![]() aus gesehen, seine Achsen gegen die
aus gesehen, seine Achsen gegen die ![]() Linie gekippt.
Linie gekippt.
![\includegraphics[width=0.7\textwidth]{relativ-020}](img1510.gif)
Die beiden Novae aus der Sicht von B.
|
Die Beschreibung von B ist ebenso gültig. Aus seiner Sicht ist A's Geschwindigkeit genau das negative von
seiner, von A aus gesehen. Deshalb ist A's 'ct'-Achse um ![]() gegen den Uhrzeigersinn geneigt.
gegen den Uhrzeigersinn geneigt.
Ereignisse, die aus B's Sicht gleichzeitig sind, sind für A nicht gleichzeitig, und umgekehrt.
| Relationen zwischen Ereignissen sind nur dann sinnvoll zu beschreiben, wenn gleichzeitig auch das Bezugssystem angegeben wird. |
| In jedem Inertialsystem gibt es konsistente Masseinheiten, die aber von Inertialsystem zu Inertialsystem verschieden sind. |
![\includegraphics[width=0.7\textwidth]{relativ-021}](img1511.gif)
Massstabsvergleich
|
Die beiden Koordinatenursprünge (B's und meiner) sollen übereinander liegen. B's Koordinatensystem ist
gekippt. Alle seine eindimensionalen Objekte sind parallel zu seiner jetzt-Achse, genauso wie alle meine
eindimensionalen Objekte parallel zu meiner jetzt-Achse sind. Zum Zeitpunkt ![]() (gilt für beide) ist
das linke Ende je eines Massstabes genau am Ursprung. Das Ende meines Massstabes ist in
(gilt für beide) ist
das linke Ende je eines Massstabes genau am Ursprung. Das Ende meines Massstabes ist in ![]() und bewegt sich weiter
zu
und bewegt sich weiter
zu ![]() . Das rechte Ende von B's Massstab beschreibt die Linie
. Das rechte Ende von B's Massstab beschreibt die Linie ![]() nach
nach ![]() . Für mich ist zur Zeit
. Für mich ist zur Zeit ![]() das Ende
von B's Massstab in
das Ende
von B's Massstab in ![]() , für ihn ist es in
, für ihn ist es in ![]() . Analog sagt B, dass mein Massstab zur Zeit
. Analog sagt B, dass mein Massstab zur Zeit ![]() in
in ![]() ist,
während es für mich in
ist,
während es für mich in ![]() ist.
ist.
Da kein Bezugssystem bevorzugt ist, muss meine Beschreibung der Situation und seine äquivalent sein.
Mein Massstab ist für B verkürzt, während seiner für mich kürzer ist. Der Verkürzungsfaktor ![]() muss für beide der
gleiche sein:
muss für beide der
gleiche sein:
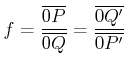 |
(4.432) |
und damit auch
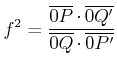
Nun ist
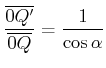
und nach dem Sinussatz
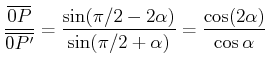
Damit ist
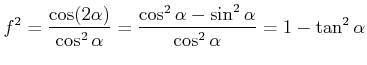 |
(4.433) |
![]() ist die Steigung der Weltline eines Punktes mit der Geschwindigkeit
ist die Steigung der Weltline eines Punktes mit der Geschwindigkeit ![]() .
.
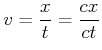
Die Steigung ist dann
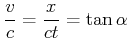
Lorentz-Kontraktion
|
In jedem gegen das Inertialsystem des Beobachters mit 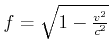 verkürzt.
verkürzt.
|
In mehreren Dimensionen entstehen durch die Laufzeiten vom Bildpunkt zum Auge zusätzliche Verzerrungen, so dass Objekte nicht einfach verkürzt erscheinen.
Als Beispiel betrachten wir eine Länge. ![]() sei die Länge gemessen im ruhenden System.
sei die Länge gemessen im ruhenden System. ![]() sei die Länge gemessen
im bewegten System. Dann ist
sei die Länge gemessen
im bewegten System. Dann ist
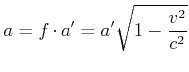
![\includegraphics[width=0.8\textwidth]{relativ-022}](img1527.gif)
Darstellung des Uhrenvergleichs
|
![\includegraphics[width=0.95\textwidth]{relativ-023}](img1528.gif)
Vergrösserte Darstellung aus der vorherigen Abbildung.
|
Aus ![]() , beziehungsweise
, beziehungsweise ![]() kann das Punktereignis Uhr zeigt 1 im anderen Bezugssystem
rekonstruiert werden. Die Argumentation ist analog wie beim Längenvergleich. Wir fordern:
kann das Punktereignis Uhr zeigt 1 im anderen Bezugssystem
rekonstruiert werden. Die Argumentation ist analog wie beim Längenvergleich. Wir fordern:
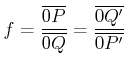
und damit
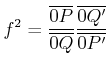
![]() ist ein rechtwinkliges Dreieck. Also ist
ist ein rechtwinkliges Dreieck. Also ist
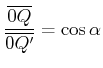
Das Dreieck ![]() ist ein allgemeines Dreieck, bei dem der Sinussatz
ist ein allgemeines Dreieck, bei dem der Sinussatz
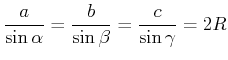
Wenn wir den Schnittpunkt
![]() mit
mit
![]() mit
mit ![]() bezeichnen, so ist das rechtwinklige
Dreieck
bezeichnen, so ist das rechtwinklige
Dreieck ![]() kongruent zu
kongruent zu ![]() . Also ist
. Also ist
![]() und
und
![]() . Der
Aussenwinkel dazu ist
. Der
Aussenwinkel dazu ist
![]() . Dieser Winkel liegt
. Dieser Winkel liegt
![]() gegenüber. Aus der
Winkelsumme im Dreieck bekommt man schliesslich
gegenüber. Aus der
Winkelsumme im Dreieck bekommt man schliesslich
![]() . Dieser Winkel liegt
. Dieser Winkel liegt
![]() gegenüber. Also ist
gegenüber. Also ist
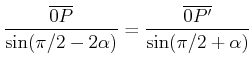
und
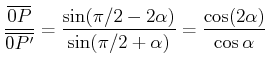
sowie
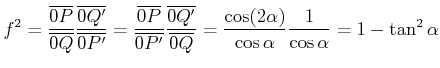
![]() ist die Steigung der Weltlinie. Also bekommen wir wieder
ist die Steigung der Weltlinie. Also bekommen wir wieder
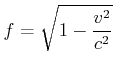 |
(4.435) |
Jeder Beobachter sieht die Uhr des anderen erst später die 1 erreichen. Bewegte Uhren gehen also langsamer wegen der Zeitdilatation.
|
|
| Zwischen zwei Punktereignissen misst derjenige Beobachter den kürzesten Zeitabstand, der sie (soweit möglich) direkt erlebt, also für den sie beide ''hier'' sind. |
| Zwischen zwei Punktereignissen misst derjenige den kürzesten Abstand, für den sie gleichzeitig erfolgen (bei ihm ist der Massstab am längsten!). |
Da wir keine Aussage über die Natur der Uhren gemacht haben, müssen wir schliessen, dass die obige Aussage für alle Prozesse gilt.
Wir können das oben gesagte auch so formulieren:
Im bewegten System (Geschwindigkeit ![]() ) am Punkt 0 gibt es zwei Ereignisse
) am Punkt 0 gibt es zwei Ereignisse ![]() und
und ![]() im Abstand
im Abstand ![]()
Im Ruhesystem ![]() ,
,![]() ,
,![]() ,
,![]() misst man
misst man
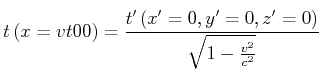 |
(4.436) |
Der Vollständigkeit halber steht unten noch das in den Lehrbüchern übliche, kaum verständliche Diagramm.
![\includegraphics[width=0.8\textwidth]{relativ-024}](img1548.gif)
Traditionelle Darstellung des Uhrenvergleichs nach (Siehe Gerthsen, Physik [Mes04, pp. 842])
|
![\includegraphics[width=0.99\textwidth]{relativ-025}](img1549.gif)
Der longitudinale relativistische Dopplereffekt. Links
ist mein Standpunkt, rechts der von B.
|
Die obige Skizze soll die Frage klären, welche Periode ![]() B misst für ein Signal, für das ich die Periode
B misst für ein Signal, für das ich die Periode ![]() messe. Die Berechnung läuft wie folgt:
messe. Die Berechnung läuft wie folgt:
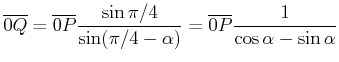
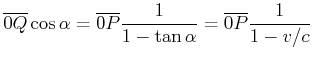
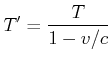
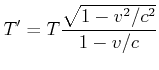
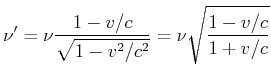
![]() würde anders argumentieren (rechte Seite von Abbildung 4.3.5)
würde anders argumentieren (rechte Seite von Abbildung 4.3.5)
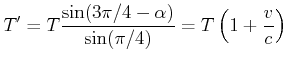
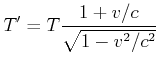
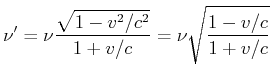
Der Dopplereffekt wird also durch die spezielle Relativitätstheorie für alle Inertialsysteme konsistent beschrieben.
Longitudinaler relativistischer Dopplereffekt:
wenn im ungestrichenen System mit der Frequenz |
Wenn eine Bewegung im Winkel ![]() schräg zur zur Beobachtungsrichtung verläuft, ist der relevante
Längenunterschied nicht
schräg zur zur Beobachtungsrichtung verläuft, ist der relevante
Längenunterschied nicht
![]() sondern
sondern
![]() . Sei
. Sei ![]() die Periodendauer im bewegten
Bezugssystem und
die Periodendauer im bewegten
Bezugssystem und
![]() die Distanz, um die sich das bewegte Bezugssystem in
die Distanz, um die sich das bewegte Bezugssystem in ![]() bewegt. Die
Zeitdilatation ist unabhängig von der Bewegungsrichtung, die Längenkontraktion jedoch nicht!
bewegt. Die
Zeitdilatation ist unabhängig von der Bewegungsrichtung, die Längenkontraktion jedoch nicht!
Wir erhalten die Beziehungen
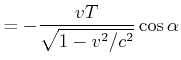 |
(4.438) | |
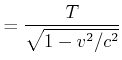 |
(4.439) | |
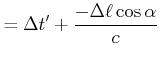 |
(4.440) |
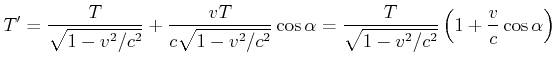
Für die Frequenzen (![]() ) gilt dann
) gilt dann
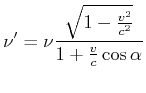 |
(4.441) |
Für ![]() bekommt man den transversalen Dopplereffekt
bekommt man den transversalen Dopplereffekt
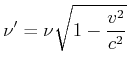 |
(4.442) |
Dies ist nichts anderes als ein Ausdruck der Zeitdilatation. Bei Schallwellen gibt es keinen transversalen Dopplereffekt.
![\includegraphics[width=0.5\textwidth]{relativ-026}](img1577.gif)
Addition von Geschwindigkeiten
|
In diesem Gedankenexperiment sollen B und ich einen Meteoriten beobachten:
Im Punkte ![]() misst B durch Rückdatierung, dass der Meteorit zur Zeit
misst B durch Rückdatierung, dass der Meteorit zur Zeit ![]() in
in ![]() und er in
und er in ![]() gewesen sind.
gewesen sind.
In dem durch ![]() gegebenen Zeitpunkt
gegebenen Zeitpunkt ![]() bestimmt B die Geschwindigkeit des Meteoriten durch
bestimmt B die Geschwindigkeit des Meteoriten durch
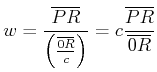 |
(4.443) |
Damit berechnet man mit dem Sinussatz
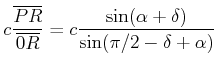 |
|||
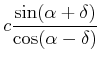 |
|||
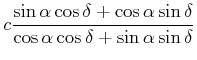 |
|||
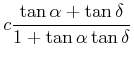 |
|||
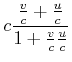 |
|||
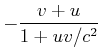 |
(4.444) |
|
Die relativistische Summe zweier Geschwindigkeiten ist
ein Wert, der um |
Es gibt die folgenden Spezialfälle:
Aus den Spezialfällen lernt man
Zwei Beispiele:
(Siehe Gerthsen, Physik [Mes04, pp. 845])
Das folgende Gedankenexperiment soll zur Ableitung des Messverfahrens für relativistische Beschleunigungen dienen.
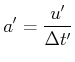
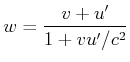
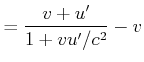 |
||
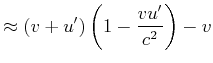 |
||
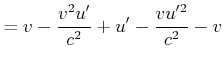 |
||
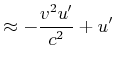 |
||
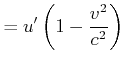 |
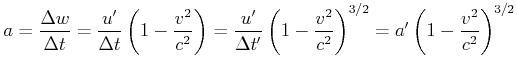
|
Die von B gemessene longitudinale Beschleunigung . |
(Siehe Tipler, Physik [Tip94, pp. 1176]) (Siehe Gerthsen, Physik [Mes04, pp. 846])
![\includegraphics[width=0.8\textwidth]{relativ-027}](img1615.gif)
|
Von dem Startturm aus werden zwei identische Raketen in kurzer Zeit auf die Geschwindigkeit ![]() oder
oder ![]() beschleunigt. Wir betrachten die Situation nach der Beschleunigung. Im Ruhesystem des Startturms
ist klar, dass der Schwerpunkt
beschleunigt. Wir betrachten die Situation nach der Beschleunigung. Im Ruhesystem des Startturms
ist klar, dass der Schwerpunkt ![]() am Ort bleibt, da wir eine bezüglich des Startturms symmetrische Situation
haben.
am Ort bleibt, da wir eine bezüglich des Startturms symmetrische Situation
haben.
Für den Reisenden in der Rakete ![]() sieht die Situation so aus:
sieht die Situation so aus:
Für den Reisenden in der Rakete ![]() sieht die Situation so aus:
sieht die Situation so aus:
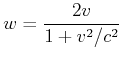
Daraus würden A und B mit klassischer Mechanik gegenseitig schliessen, dass der Schwerpunkt des Systems sich vom Startturm wegbewegt.
Nach dem 1. Einsteinschen Postulat muss die Beschreibung sowohl für das Ruhesystem des Startturms wie auch für A
(und für B) konsistent sein. Der Schwerpunkt S kann sich nur dann für ![]() immer über dem Startturm
befinden, wenn die Masse von
immer über dem Startturm
befinden, wenn die Masse von ![]() ,
, ![]() , zunimmt. Der Abstand (für grosse Zeiten) von
, zunimmt. Der Abstand (für grosse Zeiten) von ![]() zum Startturm
im Bezugssystem von
zum Startturm
im Bezugssystem von ![]() geht wie
geht wie
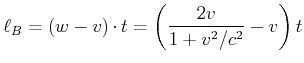 |
(4.448) |
Der Abstand des Startturms von ![]() ist in dessen Bezugssystem
ist in dessen Bezugssystem
![]() . Wir können uns auch vorstellen,
dass wir das System aus den beiden Raketen am Schwerpunkt unterstützen, die Situation ist analog zu einer
Balkenwaage. Bezüglich des Schwerpunktes muss die Summe aller Drehmomente null sein. Dies geht offensichtlich nur,
wenn die Masse von B,
. Wir können uns auch vorstellen,
dass wir das System aus den beiden Raketen am Schwerpunkt unterstützen, die Situation ist analog zu einer
Balkenwaage. Bezüglich des Schwerpunktes muss die Summe aller Drehmomente null sein. Dies geht offensichtlich nur,
wenn die Masse von B, ![]() nicht konstant, sondern von der Geschwindigkeit
nicht konstant, sondern von der Geschwindigkeit ![]() abhängt. Also
ist
abhängt. Also
ist
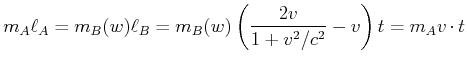 |
(4.449) |
Wir erhalten deshalb
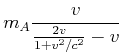 |
|||
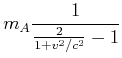 |
|||
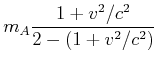 |
|||
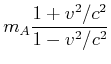 |
|||
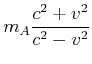 |
(4.450) |
Diese Gleichung sollte nun mit ![]() ausgedrückt werden. Wir verwenden den Trick, dass
ausgedrückt werden. Wir verwenden den Trick, dass
ist1. Dann ist
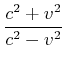 |
|||
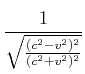 |
|||
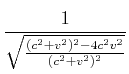 |
|||
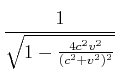 |
|||
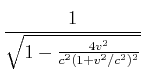 |
(4.451) |
Nun ist aber mit der Gleichung (4.65) für ![]() gerade
gerade
![]() und damit
und damit
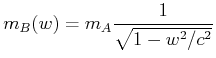 |
(4.452) |
Der Rechenweg mit dem Startturm diente dazu, eine Markierung für den Schwerpunkt zu haben. Der Startturm ist eine Hilfskonstruktion.
Die zu einem Inertialsystem mit der Geschwindigkeit
|
(Siehe Tipler, Physik [Tip94, pp. 1176]) (Siehe Gerthsen, Physik [Mes04, pp. 847])
Nach Gleichung (4.71) wird die Arbeit (Kraft mal Weg), die in eine Masse gesteckt wurde, nicht nur zur Erhöhung der Geschwindigkeit, sondern auch zur Erhöhung der Masse verwendet. Wir können Gleichung (4.71) für kleine Geschwindigkeiten entwickeln
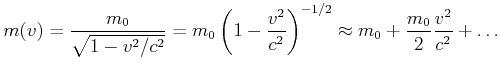 |
(4.455) |
Diese Gleichung könnte man auch als
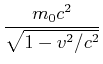 |
|||
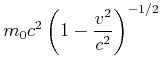 |
|||
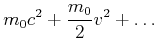 |
|||
| (4.456) |
schreiben.
Nach der relativistischen Mechanik entspricht einer (geschwindigkeitsabhängigen)
Masse die Energie
. |
Die relativistische kinetische Energie ist
Der relativistische Impuls ist analog zum klassischen Impuls definiert:
|
Die relativistische Kraft ist analog zum 2. Newtonschen Gesetz durch
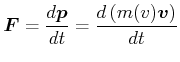 |
(4.460) |
gegeben.
Die Gesamtenergie ![]() kann wie folgt umgeformt werden
kann wie folgt umgeformt werden
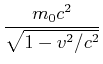 |
||||
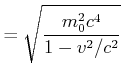 |
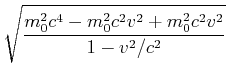 |
|||
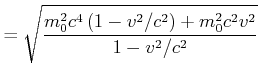 |
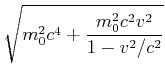 |
|||
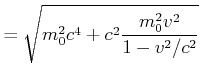 |
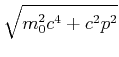 |
(4.461) |
Dieses Resultat nennt man den relativistischen Energiesatz
Wir betrachten eine Masse ![]() , die mit einer konstanten Kraft
, die mit einer konstanten Kraft
![]() beschleunigt
werde. Nach dem 2. Newtonschen Gesetz ist
beschleunigt
werde. Nach dem 2. Newtonschen Gesetz ist
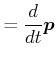 |
||
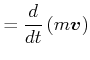 |
||
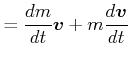 |
||
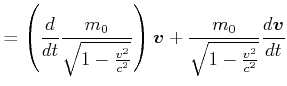 |
||
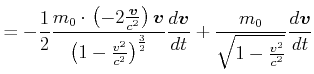 |
||
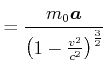 |
(4.463) |
Daraus berechnet man skalar
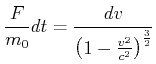 |
(4.464) |
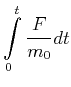 |
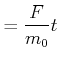 |
|
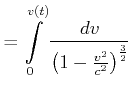 |
||
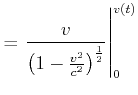 |
(4.465) | |
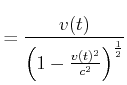 |
(4.466) |
Daraus folgt
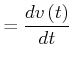 |
||
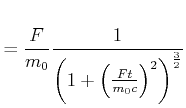 |
(4.468) |
![\includegraphics[width=0.45\textwidth]{rela_vr}](img1681.gif)
![\includegraphics[width=0.45\textwidth]{rela_ar}](img1682.gif)
Zeitverlauf der
relativistischen Geschwindigkeit (links) und der relativistischen
Beschleunigung bei konstanter Kraft.
|
Die folgenden Approximationen können gemacht werden:
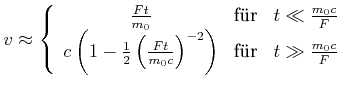 |
(4.469) |
Für die Beschleunigung erhalten wir die Approximationen
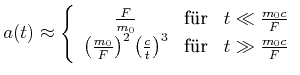 |
(4.470) |
Sowohl bei der Geschwindigkeit wie auch bei der Beschleunigung ist
![]() der
klassische Newtonsche Bereich.
der
klassische Newtonsche Bereich.
Der Impuls selber nimmt linear mit der Zeit zu, unabhängig, ob eine relativistische oder eine klassische Betrachtung durchgeführt wird. Im klassischen Fall beruht die Impulszunahme auf der Zunahme der Geschwindigkeit, im relativistischen Fall auf der Zunahme der Masse.
Die kinetische Energie
ist durch Gleichung (4.76) gegeben. Setzen wir Gleichung (4.85) (
![]() ) mit
) mit
![]() , so erhalten wir
, so erhalten wir
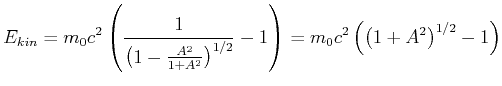 |
(4.471) |
oder
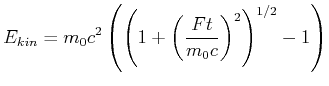 |
(4.472) |
![\includegraphics[width=0.6\textwidth]{rela_ekinr}](img1690.gif)
Verlauf der kinetischen Energie bei konstanter
Kraft im klassischen (rot) und relativistischen (grün) Fall.
|
Die Approximation ergibt
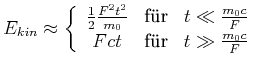 |
(4.473) |
Die kinetische Energie nimmt im relativistischen Falle nur linear mit der Zeit zu.
Mit Gleichung (4.85) kann auch die Distanz als Funktion der Zeit berechnet werden. Wir integrieren
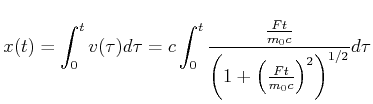 |
(4.474) |
Wir substituieren
![]() und bemerken, dass
und bemerken, dass
![]() ist, oder auch
ist, oder auch
![]() .
.
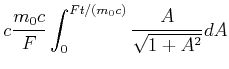 |
|||
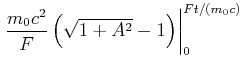 |
|||
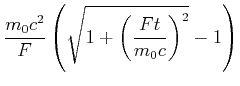 |
(4.475) |
![\includegraphics[width=0.6\textwidth]{rela_xr}](img1700.gif)
Verlauf der zurückgelegten Distanz bei konstanter
Kraft im klassischen (rot) und relativistischen (grün) Fall.
|
Wir können wieder approximieren
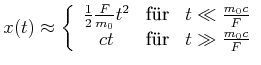 |
(4.476) |
Die weitere Rechnung zeigt, dass die relativistische Eigenzeit ![]() sich in der beschleunigten Masse
langsamer bewegt.
sich in der beschleunigten Masse
langsamer bewegt.
Wir verwenden Gleichung Gleichung (4.85) und haben dann
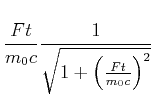 |
||
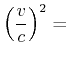 |
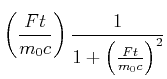 |
|
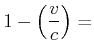 |
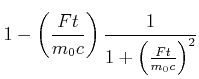 |
|
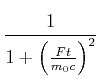 |
||
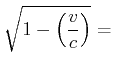 |
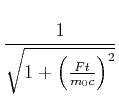 |
Mit
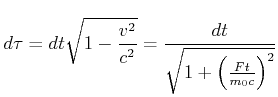 |
(4.477) |
bekommt man
![\includegraphics[width=0.6\textwidth]{rela_tau}](img1714.gif)
|
Wir kehren Gleichung (4.96) um und erhalten
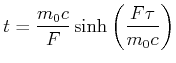
und setzen dies in den Weg ein.
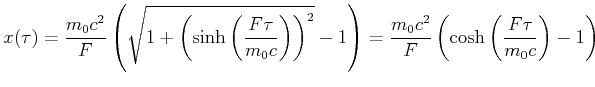 |
(4.479) |
![\includegraphics[width=0.6\textwidth]{rela_x_tau}](img1717.gif)
Zurückgelegte Strecke als Funktion der Eigenzeit.
|
|
|
(Siehe Tipler, Physik [Tip94, pp. 1157]) (Siehe Gerthsen, Physik [Mes04, pp. 853])
Die im vorherigen Abschnitt besprochenen Transformationen der zeit und der Länge lassen sich in der sogenannten Lorentz-Transformation zusammenfassen.
![\includegraphics[width=0.5\textwidth]{relativ-028}](img1718.gif)
Beschreibung eines Punktereignisses in zwei gegeneinander
bewegten Bezugssystemen
|
Das Punktereignis ![]() soll im gestrichenen Koordinatensystem (B) sowie im ungestrichenen
Koordinatensystem (A) ausgemessen werden.
soll im gestrichenen Koordinatensystem (B) sowie im ungestrichenen
Koordinatensystem (A) ausgemessen werden.
Wenn wir die obigen Beobachtungen zusammenfassen, erhalten wir
Wir rechnen nun nicht mehr mit ![]() sondern mit der Zeit
sondern mit der Zeit ![]() direkt und erhalten die Lorentz-Transformation.
direkt und erhalten die Lorentz-Transformation.
|
Die Lorentz-Transformation kann auch in Matrix-Schreibweise dargestellt werden:
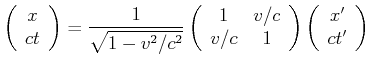 |
(4.482) |
![\includegraphics[width=0.4\textwidth]{relativ-029}](img1725.gif)
Lorentztransformation als Drehung
|
Wir erproben, was wäre, wenn wir die Lorentz-Transformation als Drehung auffassen würden. Die ![]() -Achse
würde positiv (im Gegenuhrzeigersinn) um
-Achse
würde positiv (im Gegenuhrzeigersinn) um ![]() gedreht, die
gedreht, die ![]() -Achse würde negativ (im Uhrzeigersinn) um den
gleichen Winkel
-Achse würde negativ (im Uhrzeigersinn) um den
gleichen Winkel ![]() gedreht.
gedreht.
Wir verwenden die Definition
![]() sowie
sowie
![]() und
und
![]() .
.
Dann ist
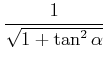 |
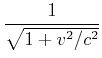 |
|||||
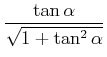 |
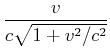 |
|||||
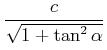 |
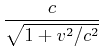 |
|||||
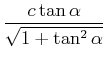 |
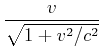 |
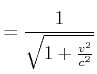 |
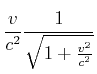 |
|||||
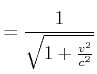 |
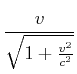 |
(4.483) |
Eingesetzt, würde man eine Transformation erhalten, die formal wie die Lorentztransformation aussieht, die aber
unter der Wurzel ein ![]() -Zeichen anstelle des geforderten
-Zeichen anstelle des geforderten ![]() -Zeichens besitzt. Die Drehgleichungen wären dann
-Zeichens besitzt. Die Drehgleichungen wären dann
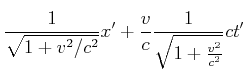 |
|||||
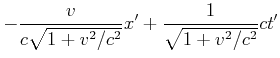 |
(4.484) |
oder
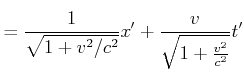 |
||
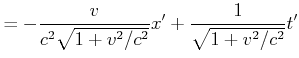 |
Diese Rotation sieht unserer Lorentz-Transformation sehr ähnlich. Die Vorzeichen unter den Wurzeln beim Cosinus
und beim Sinus sowie bei der Gleichung für ![]() stimmen nicht.
stimmen nicht.
Wenn man jedoch nicht ![]() als Zeitachse verwendet, sondern
als Zeitachse verwendet, sondern ![]() , wobei
, wobei
![]() die imaginäre Einheit ist,
bekommt man mit den obigen Drehgleichungen die Lorentz-Transformation. Dabei müssen alle Vorkommnisse von
die imaginäre Einheit ist,
bekommt man mit den obigen Drehgleichungen die Lorentz-Transformation. Dabei müssen alle Vorkommnisse von ![]() durch
durch ![]() ersetzt werden.
ersetzt werden.
Wir erhalten also
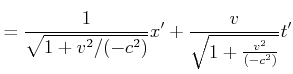 |
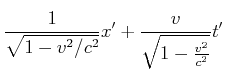 |
|||
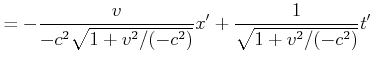 |
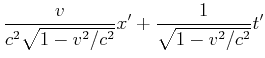 |
Der Vergleich mit Gleichung (4.98) zeigt, dass dies die Lorentztransformation ist. In einem Raum mit
den Koordinaten
![]() ist die Lorentz-Transformation nichts anderes als eine Rotation des
Koordinatensystems.
ist die Lorentz-Transformation nichts anderes als eine Rotation des
Koordinatensystems.
| Der so gemessene Abstand ist relativistisch invariant. |
Bei einer dreidimensionalen Betrachtung wird nur die der Geschwindigkeit parallele Raumkomponenten relativistisch verändert. Mit der dreidimensionalen Geschwindigkeit
![\begin{displaymath}\vec{u}=\left(
\begin{array}[c]{c}
u\\
0\\
0
\end{array}\right) \end{displaymath}](img1769.gif)
bekommen wir
Lorentz-Transformation
|
|
![\includegraphics[width=0.4\textwidth]{relativ-030}](img1783.gif)
Weltlinie beim Zwillingsparadoxon
|
Wir nehmen an, dass B sich mit der Geschwindigkeit ![]() bewegt. B's Eigenzeit ist
bewegt. B's Eigenzeit ist
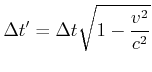
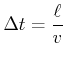
Für A ist die gesamte Reisezeit
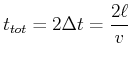
Für B dauert die Reise
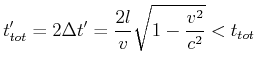
Von A aus gesehen ist B jünger nach der reise als A. Das Paradox ist: Für B bewegt sich A, warum ist A nicht jünger als B?
![\includegraphics[width=0.4\textwidth]{relativ-031}](img1788.gif)
|
Test: A und B senden regelmässig Signale. Wir nehmen an, dass die Reise
![]() weit geht. Die
gesamte Reise soll
weit geht. Die
gesamte Reise soll
![]() dauern. Die Reisegeschwindigkeit muss also
dauern. Die Reisegeschwindigkeit muss also ![]() sein. Dann ist die Zeit
für den Reisenden
sein. Dann ist die Zeit
für den Reisenden
![]() .
.
A sendet einmal pro Jahr ein Signal (
![]() ) aus, genauso wie B. B misst auf dem Hinweg die
Frequenz (Dopplereffekt)
) aus, genauso wie B. B misst auf dem Hinweg die
Frequenz (Dopplereffekt)
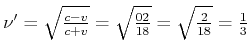 , also zwei Signale auf der ganzen Hinreise. Auf dem Rückweg mist B wegen dem Dopplereffekt die
Frequenz
, also zwei Signale auf der ganzen Hinreise. Auf dem Rückweg mist B wegen dem Dopplereffekt die
Frequenz
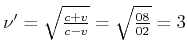 , also 18 Signale. Zusammen misst B auf
der ganzen Reise 20 Signale.
, also 18 Signale. Zusammen misst B auf
der ganzen Reise 20 Signale.
B sendet genauso Signale mit der Frequenz
![]() aus. A misst auf B's Hinweg wegen dem
Dopplereffekt Signale mit der Frequenz
aus. A misst auf B's Hinweg wegen dem
Dopplereffekt Signale mit der Frequenz
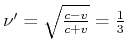 . Während 18 Jahren misst
er also total 6 Signale. Auf dem Rückweg von B misst A Signale mit der Frequenz
. Während 18 Jahren misst
er also total 6 Signale. Auf dem Rückweg von B misst A Signale mit der Frequenz
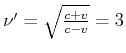 . Während 2 Jahren misst A total 6 Signale. Warum ist B jünger? B befindet sich während
seiner Reise in 2 Inertialsystemen, A nur in einem.
. Während 2 Jahren misst A total 6 Signale. Warum ist B jünger? B befindet sich während
seiner Reise in 2 Inertialsystemen, A nur in einem.
Othmar Marti