Weiter: Kreisel Oben: Mechanik starrer Körper Zurück: Statik des starren Körpers Skript: PDF-Datei Übungen: Blätter
![\includegraphics[width=0.5\textwidth]{starr-009}](img1924.gif)
|
Ein starrer Rotator wird mit einem körperfesten Koordinatensystem beschrieben.
Die Winkelgeschwindigkeit wird durch einen Vektor
![]() beschrieben. Der Betrag der
Winkelgeschwindigkeit,
beschrieben. Der Betrag der
Winkelgeschwindigkeit,
![]() gibt
gibt ![]() mal die Anzahl der Umdrehungen pro Sekunde an,
die Richtung des Geschwindigkeitsvektors die Richtung der Drehachse, wobei der Daumen der rechten Hand zur Spitze
des Vektors zeigt und die Finger die Drehrichtung angeben.
mal die Anzahl der Umdrehungen pro Sekunde an,
die Richtung des Geschwindigkeitsvektors die Richtung der Drehachse, wobei der Daumen der rechten Hand zur Spitze
des Vektors zeigt und die Finger die Drehrichtung angeben.
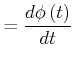 |
(5.507) |
Dabei ist ![]() der momentane Drehwinkel.
der momentane Drehwinkel. ![]() heisst die momentane Winkelgeschwindigkeit.
heisst die momentane Winkelgeschwindigkeit.
Die Geschwindigkeit des Massenpunktes
![]() am Ort
am Ort
![]() ist
ist
| (5.508) |
Jedes Massenelement
![]() hat eine kinetische Energie
hat eine kinetische Energie
![]()
Dann ist die kinetische Energie eines rotierenden Körpers gegeben durch
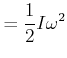 |
||
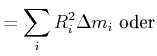 |
||
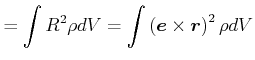 |
(5.509) |
Beweis: Wir beginnen mit der Vektoridentität
| (5.510) |
mit
![$\displaystyle =\left( \begin{array}[c]{c} a_{1} a_{2} a_{3} \end{array} \right) \times\left( \begin{array}[c]{c} b_{1} b_{2} b_{3} \end{array} \right)$](img1943.gif) |
||
![$\displaystyle =\left( \begin{array}[c]{c} a_{2}b_{3}-a_{3}b_{2} a_{3}b_{1}-a_{1}b_{3} a_{1}b_{2}-a_{2}b_{1} \end{array} \right)$](img1944.gif) |
(5.511) |
![$\displaystyle \left(
\begin{array}[c]{c}
a_{2}b_{3}-a_{3}b_{2}\\
a_{3}b_{1}-a_{1}b_{3}\\
a_{1}b_{2}-a_{2}b_{1}
\end{array} \right)^2$](img1945.gif) |
|||
| (5.512) |
| (5.513) |
Also ist
| (5.514) |
Für ein Massenelement ![]() ist die kinetische Energie
ist die kinetische Energie
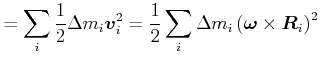 |
||
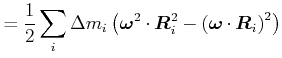 |
||
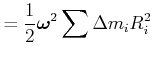 |
(5.515) |
da
![]() ist.
ist.
|
|
Der Satz von Steiner erlaubt einem, das Trägheitsmoment für eine beliebige Achse zu berechnen, wenn das Trägheitsmoment bezüglich einer dazu parallelen Achse durch den Schwerpunkt bekannt ist.
![\includegraphics[width=0.5\textwidth]{starr-010}](img1963.gif)
|
|
|
Behauptung
Es gilt der Satz von Steiner
|
Beweis: Wir berechnen die kinetische Energie eines
Massenelements ![]() . Es ist
. Es ist
![]() .
.
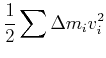 |
|||
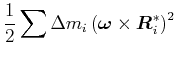 |
|||
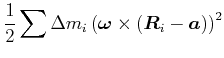 |
|||
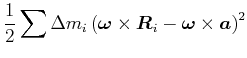 |
|||
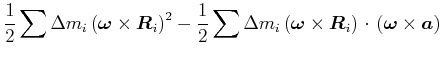 |
|||
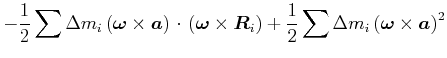 |
|||
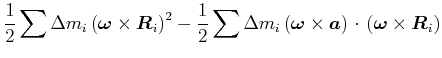 |
|||
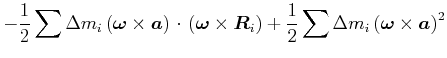 |
|||
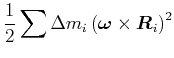 |
|||
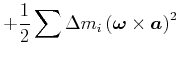 |
Der Mischterm kann umgeschrieben werden
![$\displaystyle =\left( \vec{\omega}\times\vec{a}\right) \cdot\left( \vec{\omega}\times\left[ \sum\Delta m_{i}\vec{R}_{i}\right] \right)$](img1978.gif) |
Ein Ortsvektor im Schwerpunktsystem ist
Also ist auch
![$\displaystyle \vec{\omega}\times\left[
\sum\Delta m_{i}\vec{R}_{i}\right] = \ve...
...}_i^*\right)\right]=\vec{\omega}\times\left[ \sum\Delta m_{i}\vec{r}_{i}\right]$](img1982.gif)
Nun ist aber im Schwerpunktsystem
Also ist der Term
![]() .
.
Damit wird die kinetische Energie
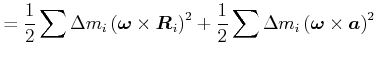 |
||
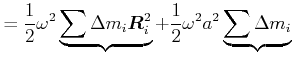 |
||
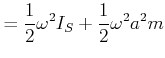 |
(5.517) |
Einige Trägheitsmomente für eine Achse durch den Schwerpunkt sind:
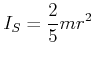 |
(5.518) |
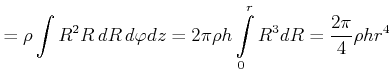 |
||
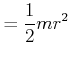 |
(5.519) |
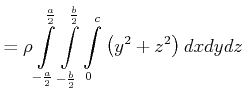 |
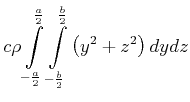 |
|||
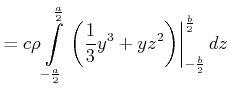 |
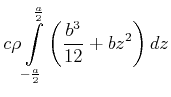 |
|||
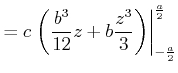 |
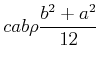 |
|||
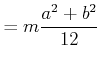 |
(5.520) |
Als Anwendung betrachten wir eine schiefe Ebene hinunterrollende Walze. Wir machen eine Energiebetrachtung.
![\includegraphics[width=0.5\textwidth]{starr-011}](img2003.gif)
Rollende Walze
|
|
|
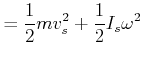 |
||
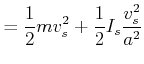 |
||
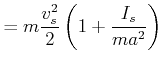 |
Also folgt für die Endgeschwindigkeit
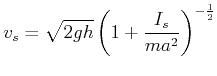 |
(5.521) |
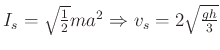
Ein Hohlzylinder rollt also langsamer eine schiefe Ebene hinunter wie ein Vollzylinder mit gleicher Masse und gleichem Durchmesser.
![\includegraphics[width=0.3\textwidth]{starr-012}](img2015.gif)
Berechnung des Drehimpulses
|
Analog zum Translations-Impuls eines Massenpunkts gilt für einen Massenpunkt
| (5.522) |
Damit gilt für den ganzen Körper
 |
(5.523) |
Die kinetische Energie eines Körpers mit dem
Drehimpuls ![]() ist
ist
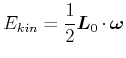 |
(5.524) |
Beweis:
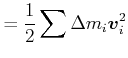 |
||
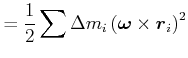 |
||
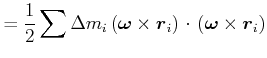 |
(5.525) |
Wir verwenden das Spatprodukt
![]() und setzen
und setzen
![]() ,
,
![]() und
und
![]() . Dann ist
. Dann ist
![]() und damit
und damit
wobei wir die Definition des Drehimpulses
![]() verwendet haben.
verwendet haben.
Bemerkung: Der Drehimpuls muss nicht parallel zur Drehachse sein. Wir betrachten den
Drehimpuls
![]() bezüglich eines Punktes 0 auf der Drehachse.
bezüglich eines Punktes 0 auf der Drehachse.
![\includegraphics[width=0.5\textwidth]{starr-013}](img2034.gif)
Aufspaltung des Drehimpulses in eine Parallel- und eine
Senkrechtkomponente
|
Sei
![]() . Dann kann der Drehimpuls in eine Komponente parallel zur
Drehachse und eine senkrecht dazu aufgespalten werden, also
. Dann kann der Drehimpuls in eine Komponente parallel zur
Drehachse und eine senkrecht dazu aufgespalten werden, also
Es gilt
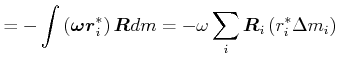 |
(5.527) |
Dabei ist
![]() die Komponente des Ortsvektors
die Komponente des Ortsvektors ![]() parallel zur Drehachse im körperfesten
Koordinatensystem.
parallel zur Drehachse im körperfesten
Koordinatensystem.
Beweis. Wir verwenden die Vektoridentität
![]() .
.
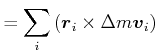 |
||
| (5.528) |
Da
![]() und
und
![]() ist.
ist.
Die Dynamik des starren Rotators bezüglich des Lagers 0 ist durch den Drallsatz gegeben.
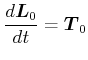 |
(5.529) |
Dabei ist
![]() das Drehmoment bezüglich des lagers 0. Bei einer gleichförmigen Rotation
das Drehmoment bezüglich des lagers 0. Bei einer gleichförmigen Rotation
![]() ist
ist
![]() i.a. nicht konstant. Es gilt
i.a. nicht konstant. Es gilt
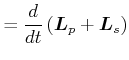 |
||
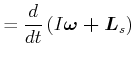 |
||
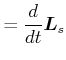 |
||
| (5.530) |
Beweis:
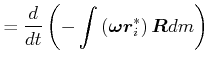 |
||
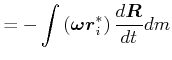 |
||
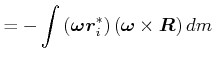 |
||
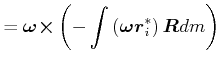 |
||
| (5.531) |
da
![]() ist.
ist.
|
|
Die Dyname auf das Drehlager im Punkt 0 ist bei einem
Rotator ohne äussere Kräfte oder Momente
| (5.532) |
wegen dem Impulssatz. Das dazugehörige Drehmoment ist
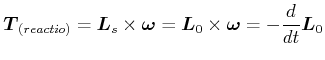 |
(5.533) |
Dabei ist
![]() der Ortsvektor des Schwerpunktes. Wir haben also eine zeitlich veränderliche Dyname.
der Ortsvektor des Schwerpunktes. Wir haben also eine zeitlich veränderliche Dyname.
|
|
Wir legen ein äusseres Drehmoment
![]() an.Dann ist
an.Dann ist
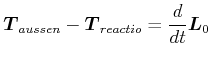 |
(5.534) |
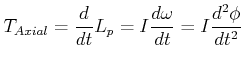 |
(5.535) |
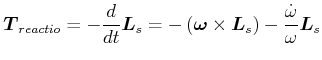 |
(5.536) |
Wirkt ein konstantes äusseres Drehmoment ![]() so gilt
so gilt
| (5.537) |
oder
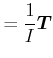 |
||
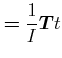 |
(5.538) |
und
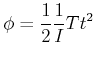 |
(5.539) |
Beispiel: rollender Zylinder
![\includegraphics[width=0.7\textwidth]{starr-014}](img2085.gif)
Rollender Zylinder
|
![]() ist die momentane Drehachse des Zylinders (Warum ist die Drehachse die Auflagelinie?). Nach dem Satz von
Steiner ist
ist die momentane Drehachse des Zylinders (Warum ist die Drehachse die Auflagelinie?). Nach dem Satz von
Steiner ist
![]()
Also ist
![]()
Die Translationsbeschleunigung des Schwerpunktes ist
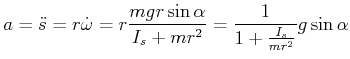 |
(5.540) |
Beispiel:
![\includegraphics[width=0.4\textwidth]{starr-015}](img2093.gif)
Drehpendel
|
Wir betrachten eine Spiralfeder und einen Rotator mit Trägheitsmoment ![]() . Es ist
. Es ist
wobei ![]() die Winkelrichtgrösse ist. Die Schwingungsdifferentialgleichung lautet dann
die Winkelrichtgrösse ist. Die Schwingungsdifferentialgleichung lautet dann
| (5.541) |
Die Lösung hat die Form
![]() mit
mit
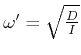 . Die Unruh in einer mechanischen Uhr ist ein Drehpendel mit
Spiralfederrückstellung.
. Die Unruh in einer mechanischen Uhr ist ein Drehpendel mit
Spiralfederrückstellung.
![\includegraphics[width=0.3\textwidth]{starr-016}](img2100.gif)
|
Die Drehmomentengleichung für das physikalische Pendel lautet
| (5.542) |
| (5.543) |
Mit
![]() wird
wird
| (5.544) |
Für kleine Winkel ![]() gilt
gilt
![]() . Also haben wir für kleine Auslenkungen die
linearisierte Bewegungsgleichung
. Also haben wir für kleine Auslenkungen die
linearisierte Bewegungsgleichung
| (5.545) |
mit
![]() . Ein physikalische Pendel
kann als mathematisches Pendel mit einer reduzierten Pendellänge
. Ein physikalische Pendel
kann als mathematisches Pendel mit einer reduzierten Pendellänge ![]() betrachtet werden.
betrachtet werden.
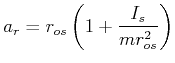 |
(5.546) |
![\includegraphics[width=0.3\textwidth]{starr-017}](img2111.gif)
Kippen eines starren Körpers
|
|
|
Hier ist
![]() und nicht bei beim Pendel
und nicht bei beim Pendel
![]() . Die Drehmomentengleichung lautet
. Die Drehmomentengleichung lautet
| (5.547) |
Sie hat die Lösungen
| (5.548) |
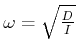 .
.
Wenn zu Beginn der Bewegung
![]() ist (Anfangsbedingung) ist die Lösung
ist (Anfangsbedingung) ist die Lösung
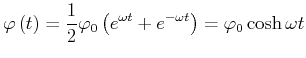 |
(5.549) |
Beispiel: Kippender Kamin
Das Trägheitsmoment eines Kamins, der um seinen Fuss rotiert, ist
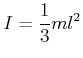 |
(5.550) |
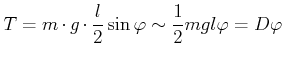 |
(5.551) |
Daraus folgt für den Betrag der Drehfrequenz
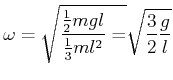 |
(5.552) |
Othmar Marti