Weiter: Kinetische Gastheorie Oben: Wärmelehre Zurück: Wärmelehre Skript: PDF-Datei Übungen: Blätter
| Dieser Stoff wurde am 07. 05. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 07. 05. 2007 PDF |
In vielen Experimenten beobachtet man, dass potentielle Energie oder kinetische Energie in Wärme umgewandelt werden kann. Beispiele hierfür sind der vollkommen plastische Stoss, Reibungswärme oder die Verlustleistung an Widerständen.
Wenn in einer Dimension zwei Massen ![]() und
und ![]() mit den Geschwindigkeiten
mit den Geschwindigkeiten
![]() und
und ![]() plastisch aufeinander stossen, wird ein Teil der kinetischen
Energie in Wärme und Deformation umgewandelt. Dieser Teil wird am einfachsten
im Schwerpunktssystem berechnet. Die Schwerpunktsgeschwindigkeit ist
plastisch aufeinander stossen, wird ein Teil der kinetischen
Energie in Wärme und Deformation umgewandelt. Dieser Teil wird am einfachsten
im Schwerpunktssystem berechnet. Die Schwerpunktsgeschwindigkeit ist
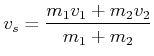 |
(4.278) |
Im Schwerpunktssystem ist die kinetische Energie der beiden Massen
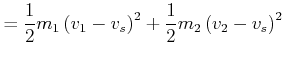 |
||
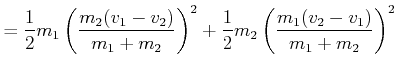 |
||
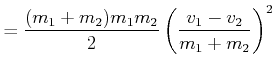 |
||
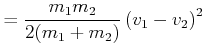 |
(4.279) |
Im vollkommen plastischen Falle wir die Energie
![]() in Deformation
oder in Wärme umgewandelt.
in Deformation
oder in Wärme umgewandelt.
|
|
Was ist Wärme? Demokrit in Griechenland stellte die Vermutung auf, dass Materie
aus kleinsten, unteilbaren Teilchen bestehen würde. Beobachtungen mikroskopisch
kleiner Partikel (Brown) führen zum Schluss, dass Flüssigkeiten und Gase aus
noch viel kleineren Teilchen (
![]() ) bestehen. Dabei sollen diese
Teilchen in einer reinen Substanz die immer gleichen Massen
) bestehen. Dabei sollen diese
Teilchen in einer reinen Substanz die immer gleichen Massen ![]() haben.
haben.
In (kristallinen) Festkörpern laufen hochfrequente Schallwellen (heute unter dem Namen Phononen bekannt). Schallwellen sind in jedem Falle an das Vorhandensein von Materie gebunden (im Vakuum gibt es keinen Schall).
| Wärmeenergie ist kinetische Energie von Atomen oder Molekülen oder anderen Teilchen. |
Jedes dieser Teilchen hat zur Zeit ![]() die Geschwindigkeit
die Geschwindigkeit ![]() und damit
die mittlere kinetische Energie
und damit
die mittlere kinetische Energie
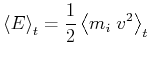 |
Da alle Teilchen identisch sein sollen wird die mittlere kinetische Energie für alle Teilchen gleich sein.
Wie wird nun erreicht, dass alle Teilchen die gleiche kinetische Energie haben? Bei elastischen Stössen werden Energien neu verteilt. Im Mittel bewirken elastische Stösse, dass kinetische Energie vom schnelleren auf das langsamere Teilchen übertragen wird, Stossprozesse gleichen also die Energie aus.
Die mittlere kinetische Energie pro Teilchen ist eine charakteristische Grösse für ein physikalisches System. Unter diesem System verstehen wir eine Anzahl gleicher oder unterschiedlicher Teilchen, die entweder als Punktmassen (ideales Gas) oder aber als ausgedehnte Körper verstanden werden.
Wenn wir zwei Systeme mit unterschiedlichen mittleren kinetischen Energien pro Teilchen in Kontakt bringen, wir Energie aus dem System mit der höheren mittleren kinetischen Energie in das andere System verschoben bis ein Gleichgewicht erreicht wird.
Aus dem Alltag wissen wir, dass wenn zwei System mit unterschiedlicher
Temperatur ![]() in Kontakt gebracht werden, diese mit der Zeit die gleiche
Temperatur erreichen. Das System mit der höheren Temperatur wird zu einer
niederen Temperatur abgekühlt, das kältere System erwärmt sich.
in Kontakt gebracht werden, diese mit der Zeit die gleiche
Temperatur erreichen. Das System mit der höheren Temperatur wird zu einer
niederen Temperatur abgekühlt, das kältere System erwärmt sich.
|
Postulat: die mittlere kinetische Energie pro Teilchen wird durch die
Temperatur |
Die Temperatur ![]() wird in Kelvin (
wird in Kelvin (![]() ) oder Grad Celsius (
) oder Grad Celsius (![]() )
gemessen. Dabei gilt
)
gemessen. Dabei gilt
| (4.280) |
Bemerkung: Grad Celsius in englisch heisst degree centigrade.
Der nullte Hauptsatz beschreibt die Relation der Temperaturen dreier Systeme
![]() ,
, ![]() und
und ![]() .
.
|
Ist ein System |
In diesem Abschnitt wollen wir unter möglichst allgemeinen Annahmen Aussagen
über die relative Häufigkeit mit der ein System im Energieintervall
![]() ,
,![]() zu finden ist. Diese Häufigkeit findet man, indem man viele System
mit den gleichen Randbedingungen untersucht und dabei die Anzahl der Teilchen,
die in das Energieintervall
zu finden ist. Diese Häufigkeit findet man, indem man viele System
mit den gleichen Randbedingungen untersucht und dabei die Anzahl der Teilchen,
die in das Energieintervall
![]() ,
,![]() fallen durch die Zahl aller
Teilchen teilt. Die so erhaltene Funktion
fallen durch die Zahl aller
Teilchen teilt. Die so erhaltene Funktion ![]() heisst Energiedichte oder
Energieverteilungsfunktion.
heisst Energiedichte oder
Energieverteilungsfunktion.
![\includegraphics[width=0.7\textwidth,keepaspectratio=true]{waerme-001}](img1023.gif)
|
Die Abbildung 4.1 zeigt eine Energieverteilungsfunktion
![]() .
.
Sei
![]() die Energieverteilungsfunktion d.h. in
die Energieverteilungsfunktion d.h. in
![]() gibt es
gibt es
![]() Teilchen. Wir betrachten nun den
Stoss eines Teilchens aus dem Energieintervall
Teilchen. Wir betrachten nun den
Stoss eines Teilchens aus dem Energieintervall
![]() mit einem Teilchen aus dem Energieintervall
mit einem Teilchen aus dem Energieintervall
![]() .
.
Die Wahrscheinlichkeit, ein Teilchen aus dem Intervall
![]() zu finden ist
zu finden ist
![]() , die
Wahrscheinlichkeit, ein Teilchen aus dem Intervall
, die
Wahrscheinlichkeit, ein Teilchen aus dem Intervall
![]() zu finden ist
zu finden ist
![]() .
.
Die Wahrscheinlichkeit
![]() vorher, diese zwei Teilchen gleichzeitig zu
finden ist
vorher, diese zwei Teilchen gleichzeitig zu
finden ist
Nach dem Stoss befinden sich die Teilchen in neuen Energieintervallen
![]() und
und
![]() . Hier ist die
Wahrscheinlichkeit
. Hier ist die
Wahrscheinlichkeit
![]() für diesen Stoss
für diesen Stoss
Die beiden Wahrscheinlichkeiten
![]() vorher und
vorher und
![]() nachher
beschreiben, wie wahrscheinlich es ist, zwei Teilchen in den jeweiligen
Zuständen zu finden.
nachher
beschreiben, wie wahrscheinlich es ist, zwei Teilchen in den jeweiligen
Zuständen zu finden.
| Physikalische Systeme bewegen sich immer in die Richtung grösserer Wahrscheinlichkeit. |
Ein thermodynamisches System, das heisst eine Anzahl (Ensemble) von Teilchen ist dann im Gleichgewicht, wenn Stösse von den ungestrichenen Energieintervallen in die gestrichenen gleich wahrscheinlich sind, wie Stösse aus den gestrichenen Energieintervallen in die ungestrichenen. Dies wird als Gleichung wie folgt ausgedrückt:
Da unser Argument unabhängig sein muss von der Breite des betrachteten Energieintervalls, kann man auch schreiben
Wenn die Energien ![]() und
und ![]() gegeben sind, können die Energien
gegeben sind, können die Energien ![]() und
und
![]() nicht mehr ganz frei gewählt werden. Die Energieerhaltung bei einem
ideal elastischen Stoss fordert:
nicht mehr ganz frei gewählt werden. Die Energieerhaltung bei einem
ideal elastischen Stoss fordert:
Hätten wir keine elastischen Stösse, würde dies bedeuten, dass die Teilchen (Atome oder Moleküle) ihre innere Struktur verändern. Zum Beispiel könnten Schwingungen angeregt werden, oder es könnten chemische Reaktionen ausgelöst werden. Im Weiteren wollen wir annehmen, dass Stösse elastisch ablaufen.
Die eine Endzustandsenergie, ![]() , kann im Intervall
, kann im Intervall
![]() frei gewählt werden.
frei gewählt werden. ![]() ist dann gegeben.
ist dann gegeben.
Wenn wir nun in Gedanken ![]() und
und ![]() festhalten und und
festhalten und und ![]() im erlaubten
Intervall variieren, sehen wir, dass bei gegebener Summe
im erlaubten
Intervall variieren, sehen wir, dass bei gegebener Summe ![]() das Produkt
der Wahrscheinlichkeiten und damit auch der Wahrscheinlichkeitsdichten konstant
sein muss. Es kann also nur von
das Produkt
der Wahrscheinlichkeiten und damit auch der Wahrscheinlichkeitsdichten konstant
sein muss. Es kann also nur von ![]() abhängen.
abhängen.
Welche mathematische Funktion hat die Eigenschaft, dass das Produkt der Funktion zweier Argumente gleich der Funktion der Summe dieser Argumente ist? Wir erkennen sie sofort, wenn wir Gleichung (4.6) logarithmieren.
Wir sehen also, dass ![]() eine lineare Funktion ist. Das heisst
eine lineare Funktion ist. Das heisst ![]() muss die Exponentialfunktion sein.
muss die Exponentialfunktion sein.
![]() ist zuerst eine Konstante mit der Dimension der Energie, die das Argument
der Exponentialfunktion dimensionslos macht.
ist zuerst eine Konstante mit der Dimension der Energie, die das Argument
der Exponentialfunktion dimensionslos macht.
Der Vorfaktor ![]() kann über die Normierungsbedingung
kann über die Normierungsbedingung
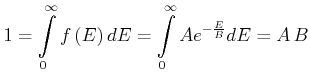 |
Also ist
![]() . Die mittlere Energie berechnet sich aus
(Integraltabelle E.1)
. Die mittlere Energie berechnet sich aus
(Integraltabelle E.1)
Offensichtlich muss in ein und demselben thermodynamischen System ![]() gleich
sein.
gleich
sein.
Die Funktion ![]() hat für
hat für ![]() bei
bei ![]() einen unbestimmten Wert. Überall
sonst ist
einen unbestimmten Wert. Überall
sonst ist ![]() . Das bedeutet, dass damit jegliche Bewegung gestoppt ist.
Man definiert nun, dass die Temperatur proportional zur mittleren kinetischen
Energie der Gasteilchen sein soll
. Das bedeutet, dass damit jegliche Bewegung gestoppt ist.
Man definiert nun, dass die Temperatur proportional zur mittleren kinetischen
Energie der Gasteilchen sein soll
| Temperatur: Mass für die mittlere kinetische Energie der Teilchen |
An diesem Punkt müssen wir aufpassen. Wir haben bei der Berechnung der
Mittelwerte in Gleichung (4.8) uns keine Gedanken gemacht, dass die
kinetische Energie ja von der vektoriellen Grösse Geschwindigkeit ![]() abhängt. Unsere Überlegung war richtig, der Vorfaktor des Resultates muss
jedoch diskutiert werden (siehe Abschnitt 4.5). Genauere
Rechnungen zeigen, dass
abhängt. Unsere Überlegung war richtig, der Vorfaktor des Resultates muss
jedoch diskutiert werden (siehe Abschnitt 4.5). Genauere
Rechnungen zeigen, dass
Die Temperatur Temperatur wird in Kelvin gemessen (nicht in Grad Kelvin!). Aus der Boltzmannverteilung Gleichung (4.10) folgt, dass es einen absoluten Temperaturnullpunkt gibt.
|
Anwendung: Die Ausströmgeschwindigkeit eines gases ins Vakuum ist im Mittel
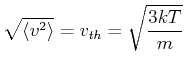 |
Üblicherweise wird die temperaturabhängige Länge eines Objektes zur Temperaturmessung ausgewertet.
| (4.289) |
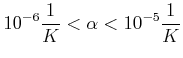 |
In der Gleichung (4.11) steht der Vorfaktor
![]() vor
vor ![]() . Dieser
Vorfaktor hängt von den Freiheitsgraden der Bewegung ab. Was ist ein
Freiheitsgrad?
. Dieser
Vorfaktor hängt von den Freiheitsgraden der Bewegung ab. Was ist ein
Freiheitsgrad?
Die Geschwindigkeit im Raum wird durch einen dreidimensionalen Vektor ![]() gegeben. Wenn der Betrag der Geschwindigkeit
gegeben. Wenn der Betrag der Geschwindigkeit
![]() gegeben ist, können
von den drei Komponenten
gegeben ist, können
von den drei Komponenten ![]() ,
, ![]() und
und ![]() noch zwei (in grenzen) frei
gewählt werden, da gilt
noch zwei (in grenzen) frei
gewählt werden, da gilt
Ausgedehnte Körper wie zum Beispiel ein ![]() -Molekül können im Raum rotiert
werden. Diese Rotation kann durch die 3 Eulerwinkel
beschrieben werden4. Neben den drei Freiheitsgraden der Translation existieren also bis
zu drei Freiheitsgrade der Rotation.
-Molekül können im Raum rotiert
werden. Diese Rotation kann durch die 3 Eulerwinkel
beschrieben werden4. Neben den drei Freiheitsgraden der Translation existieren also bis
zu drei Freiheitsgrade der Rotation.
![]() 3 Freiheitsgrade (wenn
3 Freiheitsgrade (wenn
|
Weitere Freiheitsgrade kommen hinzu, wenn die Schwingungen in den Molekülen mitberücksichtigt werden. Die quantenmechanische Betrachtung zeigt, dass bei tiefen Temperaturen diese Schwingungsfreiheitsgrade nicht angeregt werden können. Ähnlich verhält es sich mit den Freiheitsgradendie zu Rotationen um Molekülbindungen gehören.
Das ursprüngliche Argument, dass Stösse zwischen punktförmigen Gasatomen zum Erreichen eines energetischen Gleichgewichtszustandes notwendig sind, gilt für alle Freiheitsgrade.
Das Äquipartitionsgesetz besagt, dass die mittlere Energie pro Freiheitsgrad für alle Freiheitsgrade unabhängig von ihrem Charakter gleich ist.
| (4.290) | |||
| (4.291) |
wobei ![]() die Anzahl der Freiheitsgrade ist.
die Anzahl der Freiheitsgrade ist.
| Dieser Stoff wurde am 10. 5. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 10. 05. 2007 PDF Übungsblatt 05 ausgegeben am 10. 05. 2007 Lösungsblatt 05 ausgegeben am 10. 05. 2007 |
Wir haben gesehen, dass die Energie pro Molekül
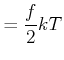 |
Ein Gasvolumen mit der Masse ![]() aus Molekülen der Masse
aus Molekülen der Masse ![]() beinhaltet dann
beinhaltet dann
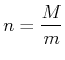 |
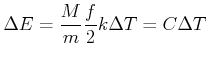 |
![$\displaystyle \left[C_V\right]= \frac{J}{K}$](img1095.gif) |
Bezieht man die Wärmekapazität auf die Masse ![]() des Körpers, so spricht man
von der spezifischen Wärmekapazität
des Körpers, so spricht man
von der spezifischen Wärmekapazität ![]()
![$\displaystyle \left[c_V\right]= \frac{J}{kg\; K} = \frac{m^2}{s^2K}$](img1098.gif) |
In der Thermodynamik ist es üblich, mit molaren Grössen zu rechnen. Die Avogadro-Zahl
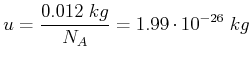 |
Die molare Wärmekapazität bei konstantem Volumen ist dann
Bei einem Festkörper ist die Anzahl Freiheitsgrade ![]() . Dann ist
. Dann ist
Bei Gasen unterscheidet man die Wärmekapazität bei konstantem Volumen ![]() und die Wärmekapazität bei konstantem Druck
und die Wärmekapazität bei konstantem Druck ![]() .
. ![]() unterscheidetr
sich von
unterscheidetr
sich von ![]() , da sie die Kompressionsarbeit enthält.
, da sie die Kompressionsarbeit enthält.
|
In der Regel sind sowohl |
Othmar Marti