Weiter: Der erste Hauptsatz Oben: Wärmelehre Zurück: Wärmeenergie und Temperaturen Skript: PDF-Datei Übungen: Blätter
Die kinetische Gastheorie berechnet für System ausser in Stössen nicht wechselwirkender Teilchen thermodynamische Grössen aus den Bewegungseigenschaften. Wir nehmen an, dass Gase aus einzelnen sich ungeordnet bewegenden Teilchen bestehen.
Die Orte der Teilchen sind weniger relevant. Deshalb konzentrieren wir uns auf die Geschwindigkeiten. Ein einzelnes Teilchen hat die vektorielle Geschwindigkeit
| (4.298) |
Dabei bedeutet zum Beispiel ![]() die Geschwindigkeitskomponente entlang der
die Geschwindigkeitskomponente entlang der
![]() -Koordinate (die durch den Einheitsvektor
-Koordinate (die durch den Einheitsvektor ![]() repräsentiert wird.
repräsentiert wird.
Jedes Atom (oder Molekül) hat seine eigene Geschwindigkeit ![]() , die auch mit
der Zeit variieren kann. Charakterisiert wird die Geschwindigkeitsverteilung,
das heisst, die Wahrscheinlichkeit, eine bestimmte Geschwindigkeit zu finden,
durch statistische Kennzahlen wie den Mittelwert
, die auch mit
der Zeit variieren kann. Charakterisiert wird die Geschwindigkeitsverteilung,
das heisst, die Wahrscheinlichkeit, eine bestimmte Geschwindigkeit zu finden,
durch statistische Kennzahlen wie den Mittelwert
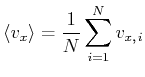 |
Da die Koordinaten ![]() ,
, ![]() und
und ![]() gleichwertig sind, gilt
gleichwertig sind, gilt
Aus Gleichung (4.21) folgt auch, dass die entsprechenden Mittelwerte summiert
werden, um den Mittelwert
![]() zu bekommen.
zu bekommen.
Stösst nun ein Atom (oder Molekül) elastisch mit der Wand, die bei ![]() senkrecht zu
senkrecht zu ![]() steht, so ist die Impulsänderung
steht, so ist die Impulsänderung
![\includegraphics[width=0.5\textwidth]{energie-001}](img1121.gif)
Berechnung des Impulsübertrages auf die Wand
|
Zur Berechnung verwenden wir die Teilchendichte
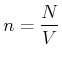 |
Die Anzahl Teilchen, die in die ![]() -Richtung fliegen, ist proportional zum
Volumen
-Richtung fliegen, ist proportional zum
Volumen
Die gesamte Impulsänderung an der Wand ist dann
Die Impulsänderung pro Zeit ist aber die Kraft auf die Fläche ![]()
Die über die Zeit gemittelte Kraft ist
Nun schliesst
![]() sowohl Teilchen, die nach rechts laufen, wie
auch solche, die nach links laufen, ein. Im Mittel läuft die Hälfte der
Teilchen nach links und die andere Hälfte nach rechts. Der Druck, die Kraft pro
Fläche ist dann
sowohl Teilchen, die nach rechts laufen, wie
auch solche, die nach links laufen, ein. Im Mittel läuft die Hälfte der
Teilchen nach links und die andere Hälfte nach rechts. Der Druck, die Kraft pro
Fläche ist dann
wobei wir Gleichung (4.23) und Gleichung (4.25) verwendet haben. Gleichung (4.27) ist bekannt unter dem Namen Grundgleichung von D. Bernoulli.
Wir wissen, wie d
![]() mit der kinetischen Energie zusammenhängt.
mit der kinetischen Energie zusammenhängt.
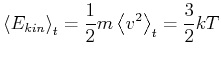 |
Mit dieser Gleichung wird Gleichung (4.27)
| (4.306) |
Bitte beachten Sie, dass wir in der Herleitung die folgenden Annahmen gemacht hatten:
In der Wärmelehre ist es auch üblich, die ideale Gaskonstante
Aus dem Gesetz für das ideale Gas, Gleichung (4.29) bekommt man drei weitere Gesetze
| Gesetz von Boyle-Mariotte | (4.310) | |||||
| Gesetz von Gay-Lussac | (4.311) | |||||
| Gesetz von Charles | (4.312) |
Diese drei Gesetze sind älter als das ideale Gasgesetz Gleichung (4.29) . deshalb werden sie häufig vor diesem behandelt. Es ist jedoch müssig, diese Gesetze zu lernen, sie sind einfache Folgerungen aus dem idealen Gasgesetz.
Othmar Marti