Weiter: Boltzmannverteilung und Diffusion Oben: Wärmelehre Zurück: Maxwell-Verteilung Skript: PDF-Datei Übungen: Blätter
Zwei Teilchen mit Radius ![]() stossen sich, wenn ihre Mittelpunkte weniger als
stossen sich, wenn ihre Mittelpunkte weniger als
![]() senkrecht zur Relativgeschwindigkeit auseinander liegen. Damit kann man
Stösse so behandeln, wie wenn die beteiligten Teilchen sich wie punktförmige
Teilchen bewegen würden, sich aber mit der Querschnittsfläche
senkrecht zur Relativgeschwindigkeit auseinander liegen. Damit kann man
Stösse so behandeln, wie wenn die beteiligten Teilchen sich wie punktförmige
Teilchen bewegen würden, sich aber mit der Querschnittsfläche ![]() , dem
Stossquerschnitt stossen.
, dem
Stossquerschnitt stossen.
![\includegraphics[width=0.4\textwidth]{hauptsatz_eins-002}](img1261.gif)
Alle Moleküle in der gezeigten Röhre mit Geschwindigkeiten entlang der
Zylinderachse stossen mit einem auf der Endfläche ruhend angenommenen Molekül.
|
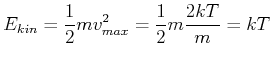 |
In der Röhre mit der Länge ![]() und dem Querschnitt
und dem Querschnitt ![]() , also dem Volumen
, also dem Volumen
![]() gibt es bei einer Teilchenzahldichte
gibt es bei einer Teilchenzahldichte ![]()
Teilchen.
Ein Stoss tritt dann auf, wenn ein Teilchen in der Röhre ist, also wenn
Die mittlere freie Weglänge für ein Teilchen, das auf ein Ensemble von ruhenden Teilchen trifft, ist dann
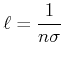 |
Eine detailiertere Betrachtungsweise (nach
[LS96]) betrachtet ein Volumen der
Oberfläche ![]() und der Dicke
und der Dicke ![]() mit der Teilchenzahldichte
mit der Teilchenzahldichte ![]() und dem
Streuquerschnitt der einzelnen Teilchen
und dem
Streuquerschnitt der einzelnen Teilchen ![]() . Die Teilchen in dem Volumen
seien in Ruhe. Bei einer dünnen Schicht überdecken die Teilchen dann die Fläche
. Die Teilchen in dem Volumen
seien in Ruhe. Bei einer dünnen Schicht überdecken die Teilchen dann die Fläche
Die Wahrscheinlichkeit ![]() , ein Teilchen zu treffen, ist
, ein Teilchen zu treffen, ist
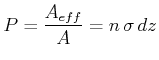 |
Wenn ![]() Teilchen auf der Oberfläche eintreffen, dann werden
Teilchen auf der Oberfläche eintreffen, dann werden
weggestreut werden. Wir können aus Gleichung (4.61) eine Differentialgleichung erster Ordnung konstruieren
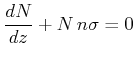 |
Diese Gleichung für die Abschwächung eines Teilchenstrahles durch ein ruhendes atomares Medium hat die Lösung
Wenn wir eine dickere Schicht betrachten, werden die unteren Teilchen durch die
oberen abgeschattet. Dies geschieht mit der Wahrscheinlichkeit
![]() . In der Tiefe
. In der Tiefe ![]() stehen
stehen
Teilchen für die Streuung zur Verfügung. Die Anzahl gestreuter Teilchen ist deshalb
Die Streurate ist deshalb
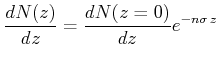 |
(4.342) |
Wie tief kann nun ein Teilchen im Mittel eindringen? Wir verwenden die allgemeine Formel
für den mit der Verteilungsfunktion (Wahrscheinlichkeitsdichte) ![]() gewichteten Mittelwert von
gewichteten Mittelwert von ![]() . Wir haben also
. Wir haben also
Dies ist das gleiche Resultat wie vorhin, aber mit Wahrscheinlichkeiten ausgerechnet.
Nun bewegen sich aber alle Teilchen. Wir müssen deshalb den Stoss zweier Teilchen in deren Schwerpunktsystem betrachten. Die relative kinetische Energie ist in dem Falle
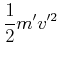 |
mit
![]() der reduzierten Masse. Wenn
der reduzierten Masse. Wenn
![]() ist, gilt
ist, gilt
![]() .
.
Wir kennen die Geschwindigkeitsverteilung im Laborsystem. Da im Mittel alle Schwerpunktsysteme die Geschwindigkeit null haben (das Gas als solches bewegt sich ja nicht) ist im Mittel die Relativgeschwindigkeit der Teilchen gleich verteilt wie die Geschwindigkeit einzelner Teilchen. Deshalb gilt:
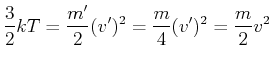 |
und deshalb
Da die Dichte der Teilchen im Schwerpunktssystem gleich ist (eine
Galileitransformation ändert keine Volumina), ist die Zeit bis zu einem Stoss
kürzer, und zwar um ![]() . Deshalb reduziert sich die mittlere
freie Weglänge auf
. Deshalb reduziert sich die mittlere
freie Weglänge auf
(mittlere freie Weglänge) |
| Dieser Stoff wurde am 24. 05. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 24. 05. 2007 PDF Übungsblatt 07 ausgegeben am 01. 06. 2007 Lösungsblatt 07 ausgegeben am 01. 06. 2007 |
Die genaue Betrachtung mit Gleichung (4.66) ergibt das gleiche Resultat. Man betrachtet die mittlere Anzahl Stösse pro Zeit eines Teilchens
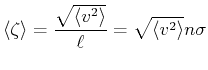 |
Wir haben dabei über das Quadrat der Geschwindigkeit gemittelt, da Richtungen
nicht relevant sind und da kinetischen Energien letztlich die relevanten
Grössen sind. Im bewegten Bezugssystem müssen wir
![]() durch
durch
![]() ersetzen.
ersetzen.
Für statistisch unabhängige Teichen mit den Geschwindigkeiten ![]() und
und
![]() ist
ist
Die Stosszahl pro Zeit ![]() (auch Stossrate genannt) im Schwerpunktsystem ist
(auch Stossrate genannt) im Schwerpunktsystem ist
Diese Stossrate ändert sich nicht, wenn wir zum Laborsystem übergehen, da bei der Galilei-Transformation die Zeit invariant ist.
Die mittlere freie Weglänge ![]() im Laborsystem ist dann durch das
Verhältnis der mittleren Geschwindigkeit
im Laborsystem ist dann durch das
Verhältnis der mittleren Geschwindigkeit
![]() zur
Stossrate
zur
Stossrate ![]()
Auch hier gibt die exakte Rechnung das gleiche Ergebnis wie die qualitative Argumentation.
![\includegraphics[width=0.5\textwidth]{hauptsatz_eins-001}](img1301.gif)
Brownsche Bewegung
|
Das Teilchen wird dauernd durch Moleküle angestossen. Wir nehmen an, dass bei jedem Stoss Impuls übertragen wird.
Zwischen zwei Stössen legt das Teilchen im Mittel die Strecke ![]() zurück[LS96]. Die Richtung dieser Bewegung
ist zufällig.
zurück[LS96]. Die Richtung dieser Bewegung
ist zufällig.
Die gesamte zurückgelegte Strecke ![]() setzt sich aus den
setzt sich aus den ![]() Einzelstrecken
Einzelstrecken ![]() zusammen.
zusammen.
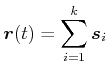 |
Wir mitteln nun über ![]() Teilchen (Scharmittel) und erhalten
Teilchen (Scharmittel) und erhalten
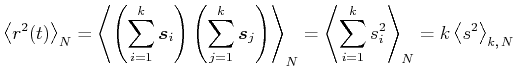 |
(4.347) |
da bei einer rein zufälligen Wahl der ![]() (dies ist die Voraussetzung)
gilt:
(dies ist die Voraussetzung)
gilt:
Wir verwenden die Verteilungsfunktion für Stösse - die Gleichung (4.63) - und erhalten mit Gleichung (4.65)
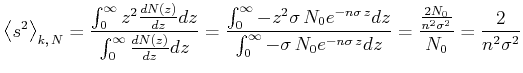 |
Da das Teilchen mit der Brownschen Bewegung sich praktisch nicht bewegt,
verwenden wir die Gleichung für die freie Weglänge mit ruhenden Stosspartnern,
also
![]() und erhalten
und erhalten
| (4.348) |
Die Anzahl Stösse berechnet sich aus der in der Zeit ![]() zurückgelegten Distanz
zurückgelegten Distanz
![]() und der Distanz zwischen zwei Stössen
und der Distanz zwischen zwei Stössen ![]() :
:
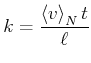 |
Damit erhalten wir
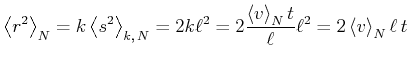 |
In drei Dimensionen sind die mittleren Verschiebungsquadrate in die ![]() -, die
-, die
![]() - und die
- und die ![]() -Richtung gleich. Damit bekommt man
-Richtung gleich. Damit bekommt man
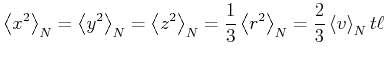 |
Andererseits gilt (ohne Beweis)
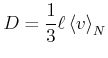 |
und
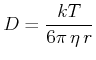 |
Wir erhalten also für das Schwankungsquadrat der Position in einer Richtung
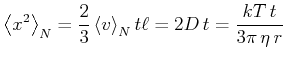 |
Diese Beziehung ist bekannt als Formel von Einstein[Ein05] und Smoluchowski[vS06]
|
Die Brownsche Bewegung von Teilchen ist auch bekannt unter dem Namen thermisches Rauschen.
Othmar Marti