Weiter: Wärmekraftmaschinen Oben: Wärmelehre Zurück: Stösse von Molekülen, Brownsche Skript: PDF-Datei Übungen: Blätter
Wir verwenden die barometrische Höhenformel (siehe Gleichung (3.56) )
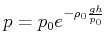 |
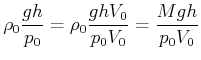 |
Hier ist
![]() die Masse des Gases. Beziehen wir alles auf ein Mol,
dann ist
die Masse des Gases. Beziehen wir alles auf ein Mol,
dann ist
![]() und
und
![]() , wobei
, wobei ![]() die Masse eines
Teilchens ist. Der Exponent wird dann
die Masse eines
Teilchens ist. Der Exponent wird dann
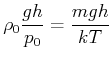 |
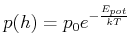 |
Boltzmann hat diese Gleichung verallgemeinert, indem er für jede
thermodynamische, von der Energie abhängige Grösse ![]() postuliert hat
postuliert hat
|
Diese Funktion ist die Boltzmannsche Verteilungsfunktion. Verwendet man
anstelle der potentiellen Energie ein Potential
![]() , lautet die
Boltzmannverteilung
, lautet die
Boltzmannverteilung
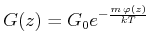 |
(4.353) |
Die Teilchendichte ist entsprechend mit der Höhe Boltzmann-verteilt.
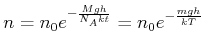 |
(4.354) |
Dabei ist ![]() die Masse eines einzelnen Teilchens. Mit dem Potential
die Masse eines einzelnen Teilchens. Mit dem Potential
![]() ausgedrückt ist
ausgedrückt ist
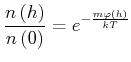 |
![\includegraphics[width=0.5\textwidth]{hauptsatz_eins-003}](img1339.gif)
Betrachtung von Teilchenströmen
|
Wir betrachten einen Teilchenstrom aus dem Volumen links von der Fläche ![]() nach rechts. Im ganzen Gebiet, sowohl links wie rechts von
nach rechts. Im ganzen Gebiet, sowohl links wie rechts von ![]() , soll die
Teilchendichte
, soll die
Teilchendichte ![]() eine Funktion von
eine Funktion von ![]() sein. Die Abhängigkeit von den anderen
Koordinaten können wir vernachlässigen, wenn
sein. Die Abhängigkeit von den anderen
Koordinaten können wir vernachlässigen, wenn ![]() genügend klein ist. In der
Nähe von
genügend klein ist. In der
Nähe von ![]() , an den Stellen
, an den Stellen ![]() können wir die Teilchenzahldichte
können wir die Teilchenzahldichte
![]() abschätzen, indem wir die Steigung
abschätzen, indem wir die Steigung
![]() an der
Stelle
an der
Stelle ![]() zur Schätzung verwenden.
zur Schätzung verwenden.
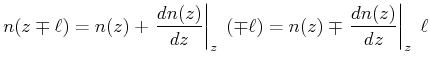 |
Analog kann der Wert der gemittelten Geschwindigkeit
![]() an den
Stellen
an den
Stellen ![]() bestimmt werden.
bestimmt werden.
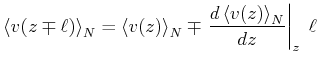 |
Die Teilchen sollen jedes eine individuelle Geschwindigkeit ![]() haben.
Wenn wir zum Mittel über alle Geschwindigkeitsbeträge wechseln, wird nur ein
Teil der Teilchen sich durch die Fläche
haben.
Wenn wir zum Mittel über alle Geschwindigkeitsbeträge wechseln, wird nur ein
Teil der Teilchen sich durch die Fläche ![]() bewegen. Wenn wir die Fläche
bewegen. Wenn wir die Fläche ![]() als eine Seite eines Würfels betrachten, in dem sich die Teilchen mit gleicher
Wahrscheinlichkeit in alle Richtungen bewegen, dann wird
als eine Seite eines Würfels betrachten, in dem sich die Teilchen mit gleicher
Wahrscheinlichkeit in alle Richtungen bewegen, dann wird ![]() aller Teilchen
die Fläche
aller Teilchen
die Fläche ![]() durchstossen. Der Teilchenfluss durch
durchstossen. Der Teilchenfluss durch ![]() in der Zeit
in der Zeit ![]() ist
dann
ist
dann
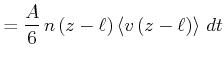 |
(4.355) | |
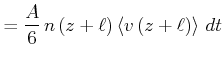 |
(4.356) |
Diese beiden Ausdrücke können mit Hilfe der Taylorentwicklung umgeschrieben werden:
![$\displaystyle = \frac{A}{6}\left[n\left(z\right)-\frac{dn(z)}{dz}\ell\right] \l...
...v\left(z\right)\right>-\frac{d\left<v\left(z\right)\right>}{dz}\ell\right] dt$](img1355.gif) |
||
![$\displaystyle =\frac{A}{6}\left[n\left(z\right)\left<v\left(z\right)\right>- n\...
...ell +\frac{dn(z)}{dz}\frac{d\left<v\left(z\right)\right>}{dz}\ell^2\right] dt$](img1356.gif) |
||
![$\displaystyle = \frac{A}{6}\left[n\left(z\right)+\frac{dn(z)}{dz}\ell\right] \l...
...v\left(z\right)\right>+\frac{d\left<v\left(z\right)\right>}{dz}\ell\right] dt$](img1357.gif) |
||
![$\displaystyle =\frac{A}{6}\left[n\left(z\right)\left<v\left(z\right)\right>+ n\...
...ell +\frac{dn(z)}{dz}\frac{d\left<v\left(z\right)\right>}{dz}\ell^2\right] dt$](img1358.gif) |
Der Netto-Teilchenstrom durch ![]() in der Zeit
in der Zeit ![]() ist
ist
![$\displaystyle = -\frac{A}{6}\left[2n\left(z\right)\frac{d\left<v\left(z\right)\right>}{dz}\ell + 2\left<v\left(z\right)\right>\frac{dn(z)}{dz}\ell \right] dt$](img1360.gif) |
||
![$\displaystyle = -\frac{A}{3}\left[n\left(z\right)\frac{d\left<v\left(z\right)\right>}{dz} + \left<v\left(z\right)\right>\frac{dn(z)}{dz} \right]\ell dt$](img1361.gif) |
Wir nehmen an, dass die Temperatur konstant sei. Dann ist die innere Energie
konstant und damit die gemittelte kinetische Energie der Teilchen damit ist
aber auch
![]() konstant (und die Ableitung nach dem Ort null).
Also ist
konstant (und die Ableitung nach dem Ort null).
Also ist
Die Grösse ![]() heisst Diffusionskoeffizient. Die Einheit von
heisst Diffusionskoeffizient. Die Einheit von ![]() ist
ist
![$\displaystyle \left[D\right] = \frac{m^2}{s}$](img1365.gif) |
Wir können Gleichung (4.79) in eine Differentialgleichung umschreiben.
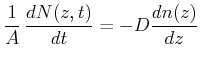 |
(4.358) |
Die transportierte Masse ist
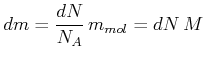 |
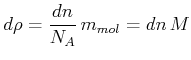 |
In drei Dimensionen lautet das 1.Ficksche Gesetz
| Durch die Diffusion wird Masse transportiert |
Das 1. Ficksche Gesetz wird oft auch mit der Teilchenstromdichte ![]() formuliert. Mit den Beziehungen
formuliert. Mit den Beziehungen
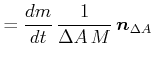 |
wobei ![]() die Teilchenmasse ist. Das erste Ficksche Gesetz lautet dann
die Teilchenmasse ist. Das erste Ficksche Gesetz lautet dann
Aus der Massenerhaltung
![]() oder der Erhaltung der Teilchenzahl
oder der Erhaltung der Teilchenzahl
![]() folgt das zweite Ficksche Gesetz
folgt das zweite Ficksche Gesetz
| Dieser Stoff wurde am 31. 05. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 21. 05. 2007 PDF |
![\includegraphics[width=0.4\textwidth]{hauptsatz_eins-004}](img1383.gif)
Teilchenströme
|
Wenn ein Teilchen, das einer Kraft ![]() ausgesetzt ist, sich durch ein Medium
mit Streuzentren bewegt, verliert es immer wieder Impuls an die Streuzentren.
Seine Geschwindigkeit wird zuerst wachsen und mit der Zeit einen konstanten
Wert annehmen, der proportional zu
ausgesetzt ist, sich durch ein Medium
mit Streuzentren bewegt, verliert es immer wieder Impuls an die Streuzentren.
Seine Geschwindigkeit wird zuerst wachsen und mit der Zeit einen konstanten
Wert annehmen, der proportional zu ![]() ist.
ist.
| (4.363) |
Die Proportionalitätskonstante ![]() heisst Beweglichkeit. Ihre
Einheit ist
heisst Beweglichkeit. Ihre
Einheit ist
![$\displaystyle \left[\mu\right] = \frac{m}{s N} = \frac{s}{kg}$](img1387.gif) |
Daraus resultiert mit der Teilchendichte ![]() die Teilchenstromdichte
die Teilchenstromdichte
Der Diffusionsstrom ist nach dem 1. Fickschen Gesetz (siehe Gleichung (4.81) ) durch
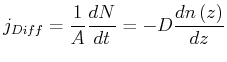 |
gegeben. Im Gleichgewicht müssen sich die beiden Ströme gerade kompensieren
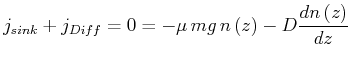 |
Die Lösung dieser Differentialgleichung ist
Diese Gleichung, hergeleitet aus der Betrachtung der Diffusion und die isotherme barometrische Höhenformel und die daraus abgeleitete Boltzmannverteilung beschreiben die gleiche Situation. Deshalb müssen die Exponenten gleich sein.
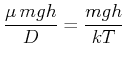 |
Othmar Marti