Weiter: Umrechnungen: Harmonischer Oszillator Oben: Vorlesungsskript PHYS2100 Grundlagen der Zurück: Berechnungen in ebenen schiefwinkligen Skript: PDF-Datei Übungen: Blätter
![\includegraphics[width=0.7\textwidth]{thermodynamik-002}](img3464.gif)
|
Bei jedem Stoss wird der Impuls um die Strecke ![]() weiter transportiert (Siehe Abbildung
I.1). Bei einem zentralen Stoss ist
weiter transportiert (Siehe Abbildung
I.1). Bei einem zentralen Stoss ist ![]() , bei einem Stoss mit dem Stossparameter
, bei einem Stoss mit dem Stossparameter ![]() ist
ist ![]() .
. ![]() hängt wie folgt von
hängt wie folgt von ![]() ab:
ab:
| (I..774) |
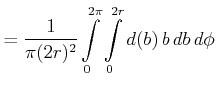 |
||
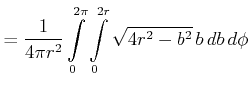 |
||
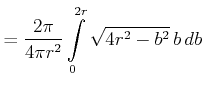 |
||
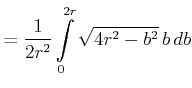 |
Othmar Marti