Umrechnung der Lösungen des gedämpften harmonischen Oszillators

Die Lösungen für den Fall $\omega_0^2>\frac{b^2}{4m^2}$ sind

$$x(t) = e^{-\frac{b}{2m}t}\left(A_{0\text{,} 1} e^{ it\sqrt{\omeg... ...c{b^2}{4m^2}}}+A_{0\text{,} 2}^{ -it\sqrt{\omega_0^2-\frac{b^2}{4m^2}}}\right)$$ (J..776)

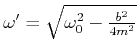Mit den Abkürzungen $B= b/(2m)$ sowie $\omega' = \sqrt{\omega_0^2-\frac{b^2}{4m^2}}$ lautet die Gleichung (J.1)

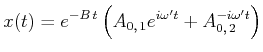$$x(t) = e^{-B t}\left(A_{0\text{,} 1} e^{ i\omega't}+A_{0\text{,} 2}^{ -i\omega' t}\right)$$ (J..777)

in der komplexen Schreibweise . Hier sind sowohl der Imaginärteil

$$x_i(t) = e^{-B t}\left(A_{0\text{,} 1}-A_{0\text{,} 2}\right)\sin(\omega' t)$$

wie auch der Realteil

$$x_r(t) = e^{-B t}\left(A_{0\text{,} 1}+A_{0\text{,} 2}\right)\cos(\omega' t)$$

Lösungen. Die vollständig geschriebene Lösung ist dann

$$x(t) = x_i(t)+x_r(t) = e^{-B t}\left[\left(A_{0\text{,} 1}-A_{0... ...omega' t)+ \left(A_{0\text{,} 1}+A_{0\text{,} 2}\right)\cos(\omega' t)\right]$$ (J..778)

Andererseits würde die Lösung mit $\cos$ geschrieben

$$x(t) = A_0 e^{-B t}\cos(\omega' t + \delta)$$ (J..779)

lauten. Hier sind $\sin$ und $\cos$ in der Phase $\delta$ versteckt. Den gemeinsamen Faktor $e^{-B t}$ können wir für die Umrechnung weglassen.

$$x(t) = A_0 e^{-B t}\left[\cos(\omega' t )\cos( \delta)-\sin(\omega' t )\sin( \delta)\right]$$ (J..780)

Wir vergleichen in den Gleichungen (J.3) und (J.5) die Vorfaktoren von $\sin$ und $\cos$ und erhalten

$$A_0\cos(\delta) = A_{0\text{,} 1}+A_{0\text{,} 2}$$ (J..781)

$$-A_0\sin(\delta) = A_{0\text{,} 1}-A_{0\text{,} 2}$$ (J..782)

Indem wir in Gleichung (J.6) die negierte zweite Zeile durch die erste teilen bekommen wir

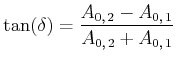$$\tan(\delta) = \frac{A_{0\text{,} 2}-A_{0\text{,} 1}}{A_{0\text{,} 2}+A_{0\text{,} 1}}$$ (J..783)

Quadrieren wir in Gleichung (J.6) beide Zeilen und addieren sie, erhalten wir

$$A_0^2\cos^2(\delta)+A_0^2\sin^2(\delta) = A_0^2 = \left(A_{0\text... ..._{0\text{,} 2}\right)^2 = 2\left(A_{0\text{,} 1}^2+A_{0\text{,} 2}^2\right)$$ (J..784)

oder, indem wir die positive Lösung verwenden,

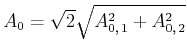$$A_0 = \sqrt{2}\sqrt{A_{0\text{,} 1}^2+A_{0\text{,} 2}^2}$$ (J..785)