Weiter: Abbildungsverzeichnis Oben: Vorlesungsskript PHYS2100 Grundlagen der Zurück: Umrechnung von thermodynamischen Funktionen Skript: PDF-Datei Übungen: Blätter
![[*]](crossref.gif) , Abschnitt 2.1.3.1:
, Abschnitt 2.1.3.1:| 0 | 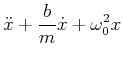 |
|||
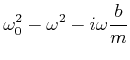 |
Dies ist eine quadratische Gleichung in ![]() . Die Lösungen sind
. Die Lösungen sind
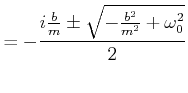 |
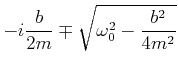 |
![[*]](crossref.gif) , Abschnitt 2.58:
, Abschnitt 2.58: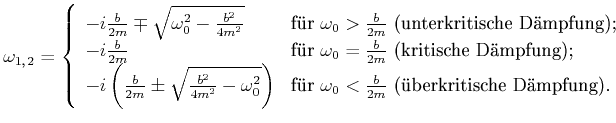 |
![[*]](crossref.gif) , Abschnitt 2.1.3.1:
, Abschnitt 2.1.3.1:
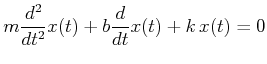 |
![[*]](crossref.gif) , Gleichung (2.83):
, Gleichung (2.83):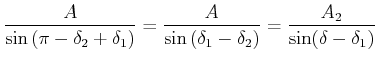 |
![[*]](crossref.gif) , Gleichung (2.82):
, Gleichung (2.82):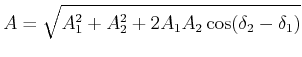 |
Othmar Marti