Weiter: Mechanik deformierbarer Medien Oben: Schwingungen und eindimensionale Wellen Zurück: Schwingungen Skript: PDF-Datei Übungen: Blätter
Im vorherigen Kapitel wurde die Lösung der Schwingungsgleichung für eine grosse Zahl gekoppelter Pendel betrachtet. Wenn bei einem solchen System ein äusseres Pendel ausgelenkt wird, breitet sich die Störung zum anderen Ende aus. Erst wenn dieser Einschwingvorgang abgeklungen ist, erhalten wir die mit den Gleichungen aus dem vorherigen Kapitel berechneten Lösungen. Die sich ausbreitende Störung im Pendelsystem nennen wir eine Welle.
Wellen können sich in Medien (Schallwellen, Seilwellen) oder auch ohne Medien (Licht, elektromagnetische Wellen) ausbreiten. Sie können sich im Raum ausbreiten, also in drei Dimensionen, auf Platten, in zwei Dimensionen oder in Seilen oder Glasfaserkabeln in einer Dimension. Wir betrachten den einfachen Fall einer Welle in einer Dimension.
| Dieser Stoff wurde am 03. 05. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 03. 05. 2007 PDF Übungsblatt 04 ausgegeben am 03. 05. 2007 Lösungsblatt 04 ausgegeben am 03. 05. 2007 |
(Siehe Tipler, Physik [Tip94, pp. 424])
![\includegraphics[width=0.8\textwidth]{seilwelle-reflexion}](img435.gif)
Reflexion einer Seilwelle wenn das Ende an der Wand
eingespannt ist
|
|
|
Wir sahen, dass bei einer Schwingung die Anfangsbedingung zweiteilig war. Der Ort und die Geschwindigkeit mussten vorgegeben werden. Genauso ist die Randbedingung einer Seilwelle durch eine von zwei Grössen charakterisiert, dem Ort und der Geschwindigkeit (erste Ableitung) oder eine höhere Ableitung. Wenn das Seil fest eingespannt ist, wie in der obigen Abbildung, ist der Ort fest und die zweite Ableitung (siehe auch den einseitig eingespannten Balken) frei. Der Wellenberg wechselt sein Vorzeichen bei der Reflexion: wir sprechen von einem Phasensprung.
![\includegraphics[width=0.8\textwidth]{seilwelle-reflexion-lose}](img436.gif)
Reflexion einer Seilwelle wenn das Ende lose befestigt ist.
|
Wenn das Seilende lose ist, ist der Ort frei, aber die Geschwindigkeit stellt sich der Anregung entsprechend ein. Hier hat die Amplitude der reflektierten Seilwelle die gleiche Phase, es gibt keinen Phasensprung.
|
Analoge Effekte treten bei elektromagnetischen Wellen auf. je nach Randbedingung
tritt bei der Reflexion ein Phasensprung von |
Die hier betrachteten Seilwellen sind Transversalwellen oder Querwellen, da die Anregung senkrecht zur Ausbreitungsrichtung ist. Licht und Seilwellen gehören zu den Transversalwellen. Bei Longitudinalwellen oder Längswellen geht die Auslenkung der Teilchen in die Richtung der Ausbreitung. Das bekannteste Beispiel einer Longitudinalwelle ist die Druckwelle bei einer Schallwelle.
![\includegraphics[width=0.8\textwidth]{Wellen-Wasserwelle}](img438.gif)
Wasserwelle
|
Mischformen von transversal- und Longitudinalwellen existieren, so zum Beispiel die oben dargestellte Wasserwelle. Ein einzelnes Wasserteilchen bewegt sich kreisförmig (eine Folge der Energieerhaltung). Dabei ist die Geschwindigkeit der Teilchen am Wellenkamm nach rechts gerichtet, wenn die Welle sich nach links ausbreitet1.
Wenn zwei Wellenberge mit entgegengesetzter Ausbreitungsrichtung sich treffen, dann addieren sich bei einem linearen System die Amplituden.
Eine Störung auf einem Seil wird nicht nur am Ende reflektiert, sondern auch, wenn die Eigenschaften des Seils sich ändern. Wenn ein Seil ab einer bestimmten Stelle weniger steif ist, ist ab der Stelle auch die Ausbreitungsgeschwindigkeit einer Störung anders. Ein Teil (im Gegensatz zur Reflexion am Ende) der Welle wird reflektiert. Dies ist analog zur Teilreflexion von Licht beim Übergang von einem Medium in das nächste.
Wir beobachten, dass die Form eines Wellenberges sich nicht ändert. Im bewegten Bezugssystem ![]() ist sie
durch
ist sie
durch
![]() gegeben. Nun bewegt sich das Maximum mit der Geschwindigkeit
gegeben. Nun bewegt sich das Maximum mit der Geschwindigkeit ![]() . Wir können die
Gleichungen der Galilei-Transformation hinschreiben
. Wir können die
Gleichungen der Galilei-Transformation hinschreiben
| (2.118) |
| (2.119) |
| (2.120) |
![\includegraphics[width=0.5\textwidth]{welle_ueberlagerung1}](img447.gif)
Überlagerung zweier Wellen mit unterschiedlichen Amplituden und
gleichem Vorzeichen. Die Zeit nimmt von oben nach unten zu.
|
Wenn wie in der obigen Zeichnung die beiden Wellen den Gleichungen
![]() und
und
![]() genügen, ist
die resultierende Wellenfunktion
genügen, ist
die resultierende Wellenfunktion
| (2.121) |
![\includegraphics[width=0.5\textwidth]{welle_ueberlagerung2}](img451.gif)
Überlagerung zweier Wellen mit gleichen
Amplituden und unterschiedlichem Vorzeichen. Die Zeit nimmt von oben nach unten zu
|
Haben die beiden Wellenberge unterschiedliche Vorzeichen, so können sie sich zu gewissen Zeiten teilweise oder, bei gleicher Amplitude, vollständig auslöschen. Obwohl in der Mitte nichts mehr von den Wellenbergen zu sehen ist, ist die Information über ihre Form und Geschwindigkeit in der kinetischen Energie der Seilstücke gespeichert.
![\includegraphics[width=0.5\textwidth]{welle_ueberlagerung}](img452.gif)
Überlagerung zweier sinusförmiger
Wellenberge mit unterschiedlichen Amplituden und gleichem Vorzeichen.
|
Das Überlagerungsprinzip gilt auch für Wellen mit beliebiger Form, hier als Sinuswelle dargestellt. Bei grossen Amplituden, also dann wenn das betrachtete System nicht mehr linear ist, gilt das Überlagerungs- oder Superpositionsprinzip nicht.
(Siehe Tipler, Physik [Tip94, pp. 429])
![\includegraphics[width=0.6\textwidth]{wellen-gleichung}](img453.gif)
Kräfteverhältnisse an einem Wellenberg in einem sich mit dem
Wellenberg sich fortbewegenden Koordinatensystem.
|
Um die Ausbreitungsgeschwindigkeit einer Störung auf einem Seil zu berechnen,
betrachten wir die Situation im Ruhesystem der Störung. In diesem System (das
nicht das Laborsystem ist) bewegt sich im Maximum das Seil mit der
Geschwindigkeit ![]() auf einer Kreisbahn mit dem Radius
auf einer Kreisbahn mit dem Radius ![]() . Die Geometrie
verlangt also, dass eine physikalische Beschleunigung der Grösse
. Die Geometrie
verlangt also, dass eine physikalische Beschleunigung der Grösse
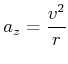 |
(2.122) |
existiert. Ursache dieser Beschleunigung des durchlaufenden Massenelementes ![]() sind die um den Winkel
sind die um den Winkel ![]() in verschiedene Richtungen zeigenden
Seilspannkräfte am Ende des Kreisbogens mit der Länge
in verschiedene Richtungen zeigenden
Seilspannkräfte am Ende des Kreisbogens mit der Länge
![]() .
. ![]() ist
die Masse pro Länge des Seils.
ist
die Masse pro Länge des Seils.
Das Kräftegleichgewicht in radialer Richtung (nach unten) ist
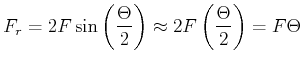 |
(2.123) |
| (2.124) |
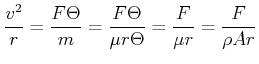 |
(2.125) |
Wir verwenden die Seilspannung
![]() und lösen die Gleichung nach
und lösen die Gleichung nach ![]() auf.
auf.
Dies ist die Ausbreitungsgeschwindigkeit einer Störung auf einem Seil oder auf einer Saite. |
Da in dieser Gleichung für ![]() keine koordinatenabhängigen Grössen vorhanden
sind, gilt sie auch für das Laborsystem des Seils.
keine koordinatenabhängigen Grössen vorhanden
sind, gilt sie auch für das Laborsystem des Seils.
Ein Seil mit einer Massenbelegung von
![]() und einer Seilspannkraft
und einer Seilspannkraft ![]() ist die
Ausbreitungsgeschwindigkeit
ist die
Ausbreitungsgeschwindigkeit
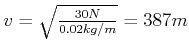 .
.
(Siehe Tipler, Physik [Tip94, pp. 431])
![\includegraphics[width=0.5\textwidth]{wellen-schnappschuss}](img470.gif)
|
In der Periodendauer ![]() bewegt sich die Welle um eine Wellenlänge
bewegt sich die Welle um eine Wellenlänge ![]() vorwärts.
Wenn wir die Frequenz
vorwärts.
Wenn wir die Frequenz ![]() einführen erhalten wir
einführen erhalten wir
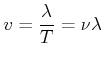 |
(2.127) |
| (2.128) |
| (2.129) |
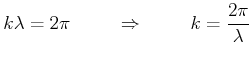 |
(2.130) |
| (2.131) |
Die Wellengleichung |
Wie schon früher berechnet, ist
![]() . Die Ausbreitungsgeschwindigkeit ist
. Die Ausbreitungsgeschwindigkeit ist
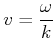 |
(2.133) |
![$\displaystyle y(x,t) = A\sin\left[2\pi\left(\frac{x}{\lambda}-\frac{t}{T}\right)\right]$](img483.gif) |
(2.134) |
(Siehe Tipler, Physik [Tip94, pp. 434])
Wenn wir ein kurzes Segment der Länge ![]() einer schwingenden Welle betrachten, dann führt dieses
eine harmonische Schwingung aus. Wenn die Wellengleichung
einer schwingenden Welle betrachten, dann führt dieses
eine harmonische Schwingung aus. Wenn die Wellengleichung
![]() ist, dann ist die
Geschwindigkeit
ist, dann ist die
Geschwindigkeit
![]() . Damit ist die kinetische
Energie des Seilsegments beim Nulldurchgang und damit auch die
Gesamtenergie
. Damit ist die kinetische
Energie des Seilsegments beim Nulldurchgang und damit auch die
Gesamtenergie
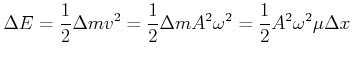 |
(2.135) |
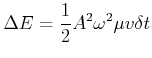 |
(2.136) |
(Siehe Tipler, Physik [Tip94, pp. 435]) (Siehe Gerthsen, Physik [Mes04, pp. 513])
Analog zu Schwingungen, deren Kombination oder Überlagerung neue Bewegungsformen ergibt, können auch Wellen überlagert werden. Dies kann sehr schön an den Wasserwellen hinter einer Hafeneinfahrt beobachtet werden.
![\includegraphics[width=0.6\textwidth]{welle_interferenz}](img493.gif)
Interferenz zweier Wellen mit der gleichen
Amplitude und der gleichen Frequenz und einer Phase, die von
|
Mathematisch setzen wir zwei Wellen an
| (2.138) |
| (2.139) |
| (2.140) |
Wir wenden die Additionstheoreme für die Winkelfunktionen an. Wir verwenden
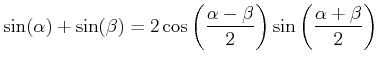 |
(2.141) |
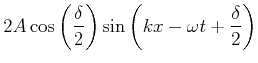 |
|
(Siehe Tipler, Physik [Tip94, pp. 435]) (Siehe Gerthsen, Physik [Mes04, pp. 513])
Wenn wir eine nach links laufende Welle
![]() und eine nach rechts laufende
Welle
und eine nach rechts laufende
Welle
![]() zur Interferenz kommen lassen, erhalten wir
zur Interferenz kommen lassen, erhalten wir
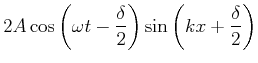 |
(2.142) |
| Stehende Wellen als Resultat zweier gegenlaufender Wellen gibt es in jedem Resonator, insbesondere in Laserresonatoren. |
Othmar Marti