![\includegraphics[width=0.8\textwidth]{interferenz-1.eps}](img495.gif)
|
Wir betrachten Wellen, die sich auf verschiedenen Wegen ausbreiten.
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Zw...
...e, bis auf eine Phase die gleiche Zeitabh{\uml a}ngigkeit haben.}\end{minipage}}](img496.gif)
Die Kohärenz von Wellen ist nur im Idealfall überall und zu jeder Zeit gegeben.
Hat eine Quelle (ein gedämpfter harmonischer Oszillator) eine Bandbreite ![]() , dann ist die
Kohärenzzeit
, dann ist die
Kohärenzzeit
![]() und
und
![]() .
.
Ist die Lichtquelle ausgedehnt (![]() ), dann gibt es nur im Winkelbereich
), dann gibt es nur im Winkelbereich
![]() eine
kohärente Überlagerung.
eine
kohärente Überlagerung.
Die Intensität muss verschieden berechnet werden, je nachdem ob die beiden Wellenzüge mit den
Amplituden ![]() und
und ![]() kohärent oder nicht sind.
kohärent oder nicht sind.
Bei kohärenten Wellen mit dem Phasenunterschied ![]() und den Amplituden
und den Amplituden ![]() und
und ![]() ist die
resultierende Amplitude
ist die
resultierende Amplitude
Wenn wir eine nach links laufende Welle
![]() und eine nach rechts laufende Welle
und eine nach rechts laufende Welle
![]() zur Interferenz kommen lassen, erhalten wir
zur Interferenz kommen lassen, erhalten wir
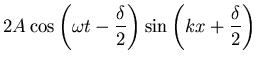 |
(6.6) |
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{We...
...f{Amplitude}\index{Amplitude} der
schw{\uml a}cheren Welle sind.}\end{minipage}}](img517.gif)
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{St...
...en gibt es in jedem Resonator, insbesondere
in Laserresonatoren.}\end{minipage}}](img518.gif)
![\includegraphics[width=0.6\textwidth]{michelson.eps}](img519.gif)
|
Beim Michelson-Interferometer wird Licht durch einen Strahlteiler in zwei Lichtwege aufgespalten. Der Weg vom
Strahlteiler zum festen Spiegel sei ![]() , der zum beweglichen
, der zum beweglichen ![]() . Deshalb ist der gesamte
Weglängenunterschied
. Deshalb ist der gesamte
Weglängenunterschied
![]() . Immer wenn
. Immer wenn ![]() ein ganzzahliges Vielfaches der
Wellenlänge
ein ganzzahliges Vielfaches der
Wellenlänge ![]() ist, tritt konstruktive Interferenz auf. Wird der bewegliche Spiegel um
ist, tritt konstruktive Interferenz auf. Wird der bewegliche Spiegel um ![]() verschoben, ändert sich
verschoben, ändert sich ![]() um
um ![]() , dann haben wir destruktive Interferenz.
, dann haben wir destruktive Interferenz.
Wenn wir das Interferometer mit einer Intensität von ![]() betreiben und wenn wir eine
Intensitätsänderung von
betreiben und wenn wir eine
Intensitätsänderung von ![]() noch messen können, dann können wir die mögliche Distanzauflösung wie
folgt berechnen:
noch messen können, dann können wir die mögliche Distanzauflösung wie
folgt berechnen:
| (6.7) |
oder umgeschrieben
| (6.8) |
Die Ableitung dieser Gleichung ist
| (6.9) |
Die maximale Steigung, also die höchste Empfindlichkeit ist
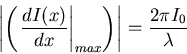 |
(6.10) |
Wir können also die Distanz
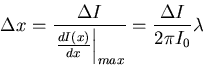 |
(6.11) |
Wenn zum Beispiel
![]() ist und
ist und
![]() ist, ist
ist, ist
![]()