



Nächste Seite: Interferenz an dünnen Schichten
Aufwärts: Interferenz und Beugung
Vorherige Seite: Phasendifferenz und Kohärenz
Diese Version ist veraltet. Eine aktuellere Version finden Sie unter http://wwwex.physik.uni-ulm.de/lehre/gk3a-2003
Unterabschnitte
(Siehe Gerthsen, Physik[GV95, 160])
Die Wellenfunktion für eine Welle in zwei oder drei Dimensionen wird wie
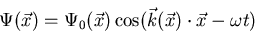 |
(6.12) |
für eine longitudinale Welle und
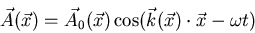 |
(6.13) |
für transversale Wellen. 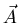 ist ein Vektor, der auch komplexe Komponenten haben kann (Die komplexen
Komponenten geben die Phasen an.). Der Vektor, der aus dem Betrag der einzelnen Komponenten gebildet wird,
gibt die Schwingungsrichtung der Welle an. Für eine transversale Welle gilt
ist ein Vektor, der auch komplexe Komponenten haben kann (Die komplexen
Komponenten geben die Phasen an.). Der Vektor, der aus dem Betrag der einzelnen Komponenten gebildet wird,
gibt die Schwingungsrichtung der Welle an. Für eine transversale Welle gilt
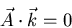 |
(6.14) |
Ebene Wellen
Materialien
Folien zur Vorlesung am 19. 06. 2002 (PDF)
Eine ebene Welle entsteht aus der allgemeinen Wellengleichung dadurch, dass die Amplitude und der
Wellenvektor nicht vom Ort abhängen. Eine ebene Transversalwelle ist durch
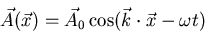 |
(6.15) |
eine Longitudinalwelle durch
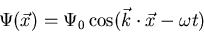 |
(6.16) |
gegeben. Ebene Wellen können durch einen Vektor, der die Ausbreitungsrichtung anzeigt, dargestellt werden.
Bei ebenen Lichwellen spricht man dann von Lichtstrahlen.
Eine weitere häufig vorkommende Form von Wellen sind die Kugelwellen. Wir können die Amplitudenabhängigkeit
durch folgende Überlegung erhalten.
- Wir denken uns eine Kugeloberfläche um die Quelle, wobei die Quelle im
Mittelpunkt der Kugel sein soll.
- Der Energiefluss pro Zeit, die Leistung, die durch die gesamte Kugeloberfläche
fliesst ist konstant, unabhängig vom Radius der Kugel.
- Damit diese Gleichung für alle
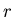 gilt muss
gilt muss
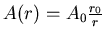 sein.
sein.
|
Amplitude und Intensität einer Kugelwelle in Abhängigkeit der Distanz 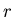 von der Quelle.
Links eine lineare, rechts eine logarithmische Darstellung. von der Quelle.
Links eine lineare, rechts eine logarithmische Darstellung.
|
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Be...
...ex{Intensit{\uml a}t} $I(r) = I_0\frac{r_0^2}{r^2}$\end{itemize}}\end{minipage}}](img545.gif)
|
Interferenz bei Moire-Mustern
|
Der erste Summand beschreibt die Interferenz, während der zweite die nur vorhanden ist, wenn die beiden
Amplituden 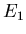 und
und 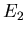 verschieden sind.
verschieden sind.
Interferenz zweier Wellen aus 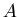 und und 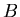
|
Aus der Zeichnung ist ersichtlich, dass der Weglängenunterschied von 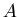 nach
nach 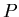 und von
und von 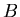 nach
nach 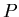
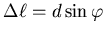 ist. Aus Gleichung (6.6) wissen wir, dass konstruktive Interferenz auftritt, wenn
ist. Aus Gleichung (6.6) wissen wir, dass konstruktive Interferenz auftritt, wenn
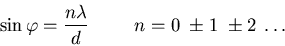 |
(6.17) |
ist. In der paraxialen Näherung (kleine 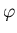 ) gilt auch
) gilt auch
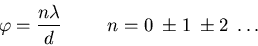 |
(6.18) |
Interferenzminima treten bei
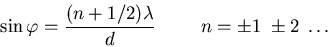 |
(6.19) |
oder, in der paraxialen Näherung (kleine 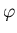 ), bei
), bei
 |
(6.20) |
Die Lage der Interferenzextrema hängen von der Wellenlänge ab.




Nächste Seite: Interferenz an dünnen Schichten
Aufwärts: Interferenz und Beugung
Vorherige Seite: Phasendifferenz und Kohärenz
Diese Version ist veraltet. Eine aktuellere Version finden Sie unter http://wwwex.physik.uni-ulm.de/lehre/gk3a-2003
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.4\textwidth]{wellen-eben.eps}](img539.gif)
![\includegraphics[width=0.45\textwidth]{welle_kugel_amplitude.eps}](img543.gif)
![\includegraphics[width=0.45\textwidth]{welle_kugel_amplitude_log.eps}](img544.gif)
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Be...
...ex{Intensit{\uml a}t} $I(r) = I_0\frac{r_0^2}{r^2}$\end{itemize}}\end{minipage}}](img545.gif)
![\includegraphics[width=0.5\textwidth]{moire.eps}](img546.gif)
![]() und
und ![]() verschieden sind.
verschieden sind.
![\includegraphics[width=0.8\textwidth]{interferenz-dreieck.eps}](img547.gif)
![]() nach
nach ![]() und von
und von ![]() nach
nach ![]()
![]() ist. Aus Gleichung (6.6) wissen wir, dass konstruktive Interferenz auftritt, wenn
ist. Aus Gleichung (6.6) wissen wir, dass konstruktive Interferenz auftritt, wenn
![]() ) gilt auch
) gilt auch
![]() ), bei
), bei