Nächste Seite: Vektoraddition von harmonischen Wellen Aufwärts: Interferenz und Beugung Vorherige Seite: Interferenz an dünnen Schichten
Diese Version ist veraltet. Eine aktuellere Version finden Sie unter http://wwwex.physik.uni-ulm.de/lehre/gk3a-2003

Interferenzmuster an einem Doppelspalt

(Siehe Tipler, Physik[Tip94, 1116])

$\framebox[\textwidth][c] {\centering\textbf{Dieser Stoff wurde am 19.6.2002 behandelt}}$

$\includegraphics[width=0.8\textwidth]{doppelspalt.eps}$
Strahlengang bei einem Doppelspalt

Aus den Interferenzbedingungen wissen wir, dass wir

$\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{ko... ...)\lambda \hspace{1cm} m = 0, \pm 1, \pm 2, \ldots \end{equation}}\end{minipage}}$

haben. Wir berechnen nun den Verlauf der Intensität.

Am Punkt ist die Phasendifferenz

$\begin{displaymath} \delta = \frac{2\pi}{\lambda}d\sin\Theta \end{displaymath}$

(6.22)

Der -te helle Streifen hat von der Achse den Abstand . Nach der Skizze ist der Winkel dann durch

$\begin{displaymath} \tan \Theta = \frac{y_m}{\ell} \end{displaymath}$

(6.23)

gegeben. Wir verwenden, dass für kleine Winkel $\Theta$ gilt: $\tan\Theta \approx \sin\Theta \approx \Theta$ . Damit folgt

$\begin{displaymath} d\sin\Theta \approx d\tan\Theta = d\frac{y_m}{\ell} \approx m\lambda \end{displaymath}$

(6.24)

Der -te helle Streifen liegt also bei

$\begin{displaymath} y_m \approx m \frac{\lambda\ell}{d} \end{displaymath}$

(6.25)

Der Abstand zweier Streifen ist

$\begin{displaymath} \Delta y = \frac{\lambda\ell}{d} \end{displaymath}$

(6.26)

Wenn wir die Amplituden der Felder verwenden (die elektrischen Felder ), können wir sagen, dass die beiden Felder $E_1 = A_0 \sin(\omega t)$ und $E_2 = A_0 \sin(\omega t + \delta)$ am Punkt interferieren.

$\begin{displaymath} E = E_1 + E_2 = A_0 \sin(\omega t)+A_0 \sin(\omega t + \delta) \end{displaymath}$

(6.27)

Mit $\sin\alpha +\sin\beta = 2\cos\left(\frac{\alpha-\beta}{2}\right)\sin\left(\frac{\alpha+\beta}{2}\right)$

bekommt man

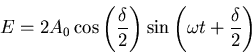$\begin{displaymath} E = 2 A_0 \cos\left(\frac{\delta}{2}\right)\sin\left(\omega t + \frac{\delta}{2}\right) \end{displaymath}$

(6.28)

Die Intensität ist dann

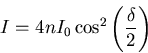$\begin{displaymath} I = 4 n I_0 \cos^2 \left(\frac{\delta}{2}\right) \end{displaymath}$

(6.29)

Mit $d\sin\Theta \approx y d/\ell$ wird die Phase

$\begin{displaymath} \delta = \frac{2\pi}{\lambda}d\sin\Theta \approx \frac{2 \pi}{\lambda}\frac{y d}{\ell} \end{displaymath}$

(6.30)

und

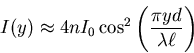$\begin{displaymath} I(y) \approx 4 n I_0 \cos^2 \left(\frac{\pi y d}{\lambda\ell}\right) \end{displaymath}$

(6.31)

$\includegraphics[width=0.25\textwidth]{doppelspalt-3.eps}$ $\includegraphics[width=0.25\textwidth]{doppelspalt-10.eps}$ $\includegraphics[width=0.25\textwidth]{doppelspalt-30.eps}$
Wellenbeugung an einem Doppelspalt. Links ist $d=3\lambda$ , in der Mitte $d=10\lambda$ und rechts $d=30\lambda$ (rechts ist der gezeigte Bildausschnitt grösser).

Othmar Marti
Experimentelle Physik
Universiät Ulm