![\includegraphics[width=0.4\textwidth]{gitter.eps}](img826.gif)
|
Beugungsgitter haben Spaltabstände ![]() in der Grössenordnung von etwa
in der Grössenordnung von etwa ![]() . Licht wird um den
Winkel
. Licht wird um den
Winkel ![]() , gegeben durch
, gegeben durch
| (6.83) |
abgelenkt. ![]() heisst die Beugungsordnung. Wenn man eine monochromatische Lichtquelle beobachtet,
stellt man fest, dass ein einzelnes Beugungsmaximum beobachtet wird. Man spricht von einer
Spektrallinie.
heisst die Beugungsordnung. Wenn man eine monochromatische Lichtquelle beobachtet,
stellt man fest, dass ein einzelnes Beugungsmaximum beobachtet wird. Man spricht von einer
Spektrallinie.
Entsprechendes gilt für die höheren Ordnungen.
Das Auflösungsvermögen eines Gitters ist als die Zahl
![]() definiert, wobei
definiert, wobei
![]() die kleinste, noch trennbare Wellenlängendifferenz ist. Damit ist
die kleinste, noch trennbare Wellenlängendifferenz ist. Damit ist
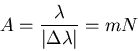 |
(6.84) |
Das Auflösungsvermögen ist proportional zur Zahl der beleuchteten Spalte ![]() . Zum Beispiel braucht man, um
die zwei Na-Linien bei
. Zum Beispiel braucht man, um
die zwei Na-Linien bei ![]() und bei
und bei ![]() aufzulösen,
aufzulösen,
![\includegraphics[width=0.6\textwidth]{blaze-gitter.eps}](img837.gif)
|
Bei einem Beugungsgitter, bei dem alle Flächen senkrecht auf der einfallenden Strahlung stehen, wird
der Hauptteil der Energie in die ![]() Ordnung gebeugt. Für spektroskopische Zwecke ist das sinnlos, da die
Wellenzerlegung bei Ordnungen größer als null auftritt. Deshalb haben moderne Gitter eine bestimmte
Oberflächenform (''blaze''), wie in der Abbildung gezeigt. Dadurch wird die Reflexion, die die
meiste Energie enthält, zu höheren Ordnungen verschoben.
Ordnung gebeugt. Für spektroskopische Zwecke ist das sinnlos, da die
Wellenzerlegung bei Ordnungen größer als null auftritt. Deshalb haben moderne Gitter eine bestimmte
Oberflächenform (''blaze''), wie in der Abbildung gezeigt. Dadurch wird die Reflexion, die die
meiste Energie enthält, zu höheren Ordnungen verschoben.
Aus der Abbildung geht hervor, dass der reflektierte Strahl mit der Einfallsrichtung den Winkel ![]() bildet, da ja
bildet, da ja
![]() gilt. Dieser Winkel soll einer bestimmten Ordnung
gilt. Dieser Winkel soll einer bestimmten Ordnung ![]() der Interferenz
entsprechen. Also muss gelten:
der Interferenz
entsprechen. Also muss gelten:
| (6.85) |
oder
| (6.86) |
Die Holographie speichert die Phaseninformation eines Lichtfeldes in einer photographischen Schicht. Sie wurde von Dennis Gabor 1947 zum ersten Male beschrieben. Um die Phaseninformation aufzuzeichnen ist es notwendig, die Interferenz des aufzuzeichnenden Lichtfeldes mit einem Referenzlichtfeld aufzuzeichnen.
![\includegraphics[width=0.8\textwidth]{hologramm-1.eps}](img843.gif)
|
Bei der Aufzeichnung des Hologramms wird eine möglichst monochromatische Lichtquelle, also zum Beispiel ein
Laser auf zwei Pfade aufgeteilt.Der eine Pfad beleuchtet das Objekt, dessen gestreutes Licht mit der
Amplitude ![]() die Photoplatte beleuchtet. Der zweite Strahl wird über ein Spiegelsystem als
Referenzstrahl
die Photoplatte beleuchtet. Der zweite Strahl wird über ein Spiegelsystem als
Referenzstrahl ![]() auf die Photoplatte gebracht, deren Ebene mit
auf die Photoplatte gebracht, deren Ebene mit ![]() bezeichnet wird und die
identisch mit der Ebene
bezeichnet wird und die
identisch mit der Ebene ![]() , also der
, also der ![]() -Ebene ist. Auf dem Hologramm wird die Intensitätsverteilung
-Ebene ist. Auf dem Hologramm wird die Intensitätsverteilung
![]() resultierend aus der Interferenz von
resultierend aus der Interferenz von ![]() und
und ![]() in eine dazu proportionale Schwärzung
umgewandelt.
in eine dazu proportionale Schwärzung
umgewandelt.
![\includegraphics[width=0.8\textwidth]{hologramm-2.eps}](img850.gif)
|
Das Hologramm in der ![]() -Ebene wird anschliessend mit monochromatischem Licht der gleichen
Wellenlänge,
-Ebene wird anschliessend mit monochromatischem Licht der gleichen
Wellenlänge, ![]() beleuchtet. Es entstehen drei Strahlen, nämlich
beleuchtet. Es entstehen drei Strahlen, nämlich
![\includegraphics[width=0.8\textwidth]{hologramm-3.eps}](img852.gif)
|
Die Berechnung dieser Effekte beginnt mit dem Referenzstrahl ![]()
| (6.87) |
Dabei ist ![]() die örtlich variierende Phase, da
die örtlich variierende Phase, da ![]() nicht senkrecht auf
nicht senkrecht auf ![]() fällt. Bei einer
ebenen Welle, die mit dem Winkel
fällt. Bei einer
ebenen Welle, die mit dem Winkel ![]() zur Senkrechten auf die Hologrammebene fällt wäre
zur Senkrechten auf die Hologrammebene fällt wäre
| (6.88) |
Die vom Objekt gestreute Welle ist
| (6.89) |
wobei sowohl ![]() und
und
![]() komplizierte Funktionen des Ortes sind. Die Intensität
in der Hologrammebene
komplizierte Funktionen des Ortes sind. Die Intensität
in der Hologrammebene ![]() ist durch
ist durch
| (6.90) | |||
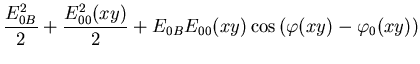 |
gegeben. Der Kontrast, gegeben durch
![]() ist
ist
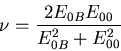 |
(6.91) |
Die Schwärzung der holographischen Emulsion soll proportional zu ![]() sein. Indem wir mit der
Rekonstruktionswelle
sein. Indem wir mit der
Rekonstruktionswelle
| (6.92) |
das Hologramm beleuchten, erhalten wir eine Amplitudenverteilung gerade hinter dem Hologramm von
![]() . Ohne konstante Faktoren ist das Resultat
. Ohne konstante Faktoren ist das Resultat
![$\displaystyle \frac{1}{2}E_{0R}\left(E_{0B}^2+E_{00}^2(x,y)\right)\cos[\omega t +\varphi (x,y)]$](img868.gif) |
|||
![$\displaystyle +\frac{1}{2}E_{0R}E_{0B}E_{00}(x,y)\cos[\omega t +2\varphi (x,y)-\varphi _0(x,y)]$](img869.gif) |
|||
![$\displaystyle +\frac{1}{2}E_{0R}E_{0B}E_{00}(x,y)\cos[\omega t +\varphi _0(x,y)]$](img870.gif) |
(6.93) |
Wie oben diskutiert existieren drei Terme.
Hologramme mit ebenen Wellen als Referenz- und Rekonstruktionswellen haben eine beschränkte Auflösung. Dies ist ersichtlich bei der Betrachtung des Hologramms einer punktförmigen Quelle. Die Interferenz zwischen einer ebenen Welle und einer Kugelwelle ergibt das gleiche Muster wie das Beugungsmuster an einer kreisförmigen Öffnung. Dort und auch hier nimmt der Abstand der Beugungsmaxima nach aussen ab. Indem das Hologramm mit Licht etwa der gleichen Krümmung wie die Objektwelle beleuchtet wird kann diese Abnahme vermieden werden (Fourier-Holographie).
Neben den besprochenen flächigen Hologrammen gibt es auch Volumenhologramme. Dort wird ein dreidimensionales Beugungsgitter analog zu einem Kristall erzeugt. Diese Hologramme können auch mit weissem Licht beleuchtet werden.
Durch die Überlagerung zweier Hologramme können interferometrische Messungen der Verschiebung von Objekten im
![]() -Bereich durchgeführt werden.
-Bereich durchgeführt werden.