Beugung und Auflösung

Wir verwenden die Tatsache, dass optische Systeme in den einfachsten Fällen lineare Systeme sind. Wenn

und

Intensitätsverteilungen senkrecht zur optischen Achse sind, und

die Ausgangsverteilung und

die Bildverteilung ist, schreibt man für die Abbildung

Die Abbildung ist linear, das heisst, wenn $f_1 \rightarrow g_1$ und $f_2 \rightarrow g_2$ ist, ist

$\begin{displaymath} a_1 \cdot f_1 + a_2 \cdot f_2 \rightarrow a_1 \cdot g_1 + a_2 \cdot g_2 \end{displaymath}$

(6.67)

$\displaystyle f(x,y)$	$\textstyle =$	$\displaystyle \int \hat{f}(u,v)e^{2\pi i [ux+vy]}dudv$
$\displaystyle \hat{f}(u,v)$	$\textstyle =$	$\displaystyle \int f(x,y) e^{-2\pi i [ux+vy]}dxdy$	(6.68)

Wir schreiben $\vec x = (x,y)$ und $\vec u = (u,v)$ Die Fouriertransformation lässt sich dann kompakt schreiben als

$\displaystyle f(\vec x)$	$\textstyle =$	$\displaystyle \int \hat{f}(\vec u)e^{2\pi i [\vec u \cdot \vec ]}d\vec u$
$\displaystyle \hat{f}(\vec u)$	$\textstyle =$	$\displaystyle \int f(\vec x) e^{-2\pi i [\vec u \cdot \vec x]}d\vec x$	(6.69)

Impulsantwort und Faltungssatz

Ein Lichtfleck an der Position $\vec x'$ der Eingangsebene erzeugt eine Intensitätsverteilung in der Ausgangsebene, die sowohl vom Beobachtungspunkt $\vec x$ wie auch von $\vec x'$ abhängt. Die Impulsantwort ist

$\begin{displaymath} h(\vec x,\vec x') = h(\vec x - \vec x') \end{displaymath}$

(6.71)

gilt. Bei einem kontinuierlichen linearen optischen System gilt zwischen der Bildebene und der Eingangsebene die Beziehung

$\begin{displaymath} g(\vec x) = \int\int f(\vec x') h(\vec x -\vec x') d\vec x' = f(\vec x) \star h(\vec x) \end{displaymath}$

(6.72)

Dies ist das Faltungstheorem aus der Fourieroptik. Im Fourierraum wird aus einer Faltung eine Multiplikation, also

$\begin{displaymath} \hat{g}(\vec u) = \hat{h}(\vec u) \hat{f}(\vec u) \end{displaymath}$

(6.73)

Wenn die optische Übertragung kohärent verläuft, dann verwendet man die oben definierte kohärente Übertragungsfunktion, die Amplituden verknüpft. Ist die Übertragung nicht kohärent, muss man mit Intensitäten rechnen.

$\includegraphics[width=0.8\textwidth]{beugung-linse.eps}$

Berechnung der Beugung an einer Öffnung

Das entstehende Beugungsbild eines Punktes ist das Fraunhofersche Beugungsmuster der Blendenöffnung. Die inkohärente Impulsantwort wird

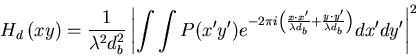$\begin{displaymath} H_d\left(x,y\right) = \frac{1}{\lambda^2d_b^2}\left\vert\in... ... d_b}+\frac{y\cdot y'}{\lambda d_b}\right)}dx'dy'\right\vert^2 \end{displaymath}$

(6.74)

Dies bedeutet, dass

das Betragsquadrat der Fouriertransformation der Pupillenfunktion

ist.

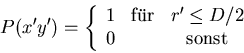$\begin{displaymath} P(x',y') = \left\{\begin{array}{ccc} 1 & \textrm{f{\uml u}... ... r' \leq D/2 \\ 0 & & \textrm{sonst} \\ \end{array}\right. \end{displaymath}$

(6.75)

wobei

den Durchmesser der Öffnung und $r' = \sqrt{x'^2+y'^2}$ den Radius darstellt.

$\displaystyle r'$	$\textstyle =$	$\displaystyle \sqrt{x'^2+y'^2}$
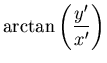$\displaystyle \Theta'$	$\textstyle =$	$\displaystyle \arctan\left(\frac{y'}{x'}\right)$	(6.76)

$\displaystyle r$	$\textstyle =$	$\displaystyle \sqrt{x^2+y^2}$
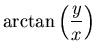$\displaystyle \Theta$	$\textstyle =$	$\displaystyle \arctan\left(\frac{y}{x}\right)$	(6.77)

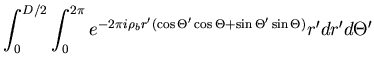$\displaystyle \hat{P}(\rho_b)$	$\textstyle =$	$\displaystyle \int_0^{D/2}\int_0^{2\pi} e^{-2\pi i \rho_b r' \left(\cos\Theta'\cos\Theta+\sin\Theta'\sin\Theta\right)}r'dr'd\Theta'$
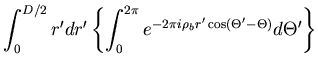	$\textstyle =$	$\displaystyle \int_0^{D/2} r'dr' \left\{\int_0^{2\pi} e^{-2\pi i \rho_b r' \cos\left(\Theta'-\Theta\right)}d\Theta'\right\}$	(6.78)

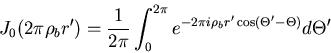$\begin{displaymath} J_0(2\pi\rho_b r') = \frac{1}{2\pi} \int_0^{2\pi} e^{-2\pi i \rho_b r' \cos\left(\Theta'-\Theta\right)}d\Theta' \end{displaymath}$

(6.79)

die sogenannte Besselfunktion nullter Ordnung. Die Fouriertransformation einer runden Pupille wird also

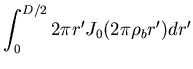$\displaystyle \hat{P}(\rho_b)$	$\textstyle =$	$\displaystyle \int_0^{D/2} 2\pi r' J_0(2\pi \rho_b r')dr'$
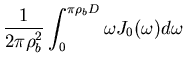	$\textstyle =$	$\displaystyle \frac{1}{2\pi \rho_b^2}\int_0^{\pi\rho_b D} \omega J_0(\omega)d\omega$
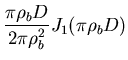	$\textstyle =$	$\displaystyle \frac{\pi \rho_b D}{2\pi\rho_b^2} J_1 (\pi \rho_b D)$
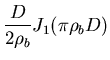	$\textstyle =$	$\displaystyle \frac{D}{2\rho_b} J_1 (\pi \rho_b D)$	(6.80)

$J_1(\alpha) = \int_0^\alpha \omega J_0(\omega)d\omega$ ist die Besselfunktion erster Ordnung. Mit $r = \lambda d_b \rho_b$ , $\Theta$ und $S = \pi D^2/4$ , der Pupillenfläche, bekommt man für die komplexe Amplitude

$\displaystyle \psi(r)$	$\textstyle =$	$\displaystyle \hat{P}(\rho_b) = S \left[\frac{2 J_1\left(\pi\rho_b D\right)}{\pi \rho_b D}\right]$
$\displaystyle I(r)$	$\textstyle =$	$\displaystyle \left\vert\psi(r)\right\vert^2 = S^2 \left[\frac{2 J_1\left(\pi\rho_b D\right)}{\pi \rho_b D}\right]^2$	(6.81)

$\includegraphics[width=0.48\textwidth]{bessel1.eps}$ $\includegraphics[width=0.48\textwidth]{airy-fkt.eps}$

Die Beugung an einer ringförmigen Apertur.

Bei der Beugungsfigur an einer kreisförmigen Öffnung mit dem Durchmesser

ist das erste Minimum bei $\sin\Theta = 1.22 \frac{\lambda}{d}$ .

$\includegraphics[width=0.8\textwidth]{aufloesung4.eps}$

Abbildung zweier punktförmiger, inkohärenter Quellen durch eine Blende mit der Öffnung

$\begin{displaymath} \sin\alpha_K = 1.22 \frac{\lambda}{d} \end{displaymath}$

(6.82)

gegeben ist, fällt das Minimum der einen Beugungsfigur gerade auf das Maximum der anderen. Das obige Kriterium wird das Rayleighsche Auflösungskriterium genannt.

$\includegraphics[width=0.5\textwidth]{aufloesung1.eps}$

Form der Intensität bei der Überlagerung zweier inkohärenter Punktquellen. Der Abstand variiert von (rot) bis (blau) in Schritten von .

Diese Abbildung zeigt, dass die Definition des Auflösungsvermögens an das mögliche Signal-Rausch-Verhältnis gebunden ist. Mit modernen Detektoren mit 16 Bit Auflösung sind deshalb leicht bessere Grenzen der Auflösung möglich.

$\includegraphics[width=0.48\textwidth]{aufloesung2.eps}$ $\includegraphics[width=0.48\textwidth]{aufloesung3.eps}$

Querschnitt zweier inkohärenter Punktquellen als Funktion des Abstandes (links) und Bild der Intensitätsverteilung bei einem Abstand von .

Wenn das zu untersuchende Objekt in ein Medium mit dem Brechungsindex

eingebettet ist, dann verbessert sich die Auflösung auf $\sin\alpha_K = 1.22 \frac{\lambda}{n\cdot d}$ , da in diesem Medium die Wellenlänge ja $\lambda' = \lambda/n$ ist.


$\left[2J_1(\pi X)/(\pi X)\right]^2$