
Weiter: Symbole Oben: Resonatoren und ihre Lichtmoden Zurück: Resonatoren mit sphärischen Spiegeln Skript: PDF-Datei Übungen: Blätter
(Siehe Yariv, Quantum Electronics [Yar75, pp. 106])
Als Vorstufe betrachten wir die durch eine Linse induzierte
abstandsabhängige Phasendifferenz für paraxiale
Strahlen. Die Linsenkrümmung sei ![]() . Die
. Die
![]() -Ebene sei senkrecht zur optischen Achse. Dann ist die Dicke der
Sammellinse durch
-Ebene sei senkrecht zur optischen Achse. Dann ist die Dicke der
Sammellinse durch
![]() gegeben. Der optische Weg setzt sich dann aus
gegeben. Der optische Weg setzt sich dann aus
![]() zusammen. Die Zeit, die Das Licht für das durchlaufen dieser Strecke benötigt
ist
zusammen. Die Zeit, die Das Licht für das durchlaufen dieser Strecke benötigt
ist
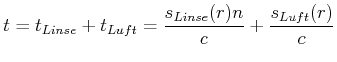 |
(6..18) |
Mit
![]() und unter Weglassung aller konstanten Terme
bekommt man
und unter Weglassung aller konstanten Terme
bekommt man
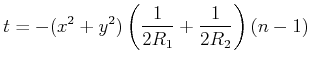 |
(6..19) |
Mit
![]() ist das Resultat
ist das Resultat
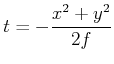 |
(6..20) |
Wenn wir mit ![]() die Amplitudenverteilung links von der Linse
und mit
die Amplitudenverteilung links von der Linse
und mit ![]() die Verteilung rechts von der Linse beschreiben,
gilt
die Verteilung rechts von der Linse beschreiben,
gilt
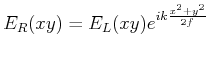 |
(6..21) |
Den gleichen Effekt erreicht man mit einem Medium, das die folgende Variation des Brechungsindexes hat
![$\displaystyle n(x,y) = n_0\left[1-\frac{k_2}{k}(x^2+y^2)\right]$](img1282.gif) |
(6..22) |
Mit dem Fermatschen Prinzip in differentieller Schreibweise
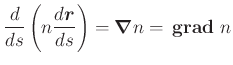 |
(6..23) |
kann die Trajektorie des Lichtstrahls ausgerechnet werden. Dabei ist ![]() die
Weglänge entlang des Lichtstrahls. Bei paraxialen
Strahlen kann
die
Weglänge entlang des Lichtstrahls. Bei paraxialen
Strahlen kann ![]() durch
durch ![]() ersetzt werden. Damit ist
die Gleichung für paraxiale Strahlen
ersetzt werden. Damit ist
die Gleichung für paraxiale Strahlen
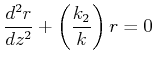 |
(6..24) |
Wenn der Strahl am Eingang die Position ![]() und die Steigung
und die Steigung ![]() hat, ist
die Lösung
hat, ist
die Lösung
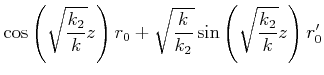 |
|||
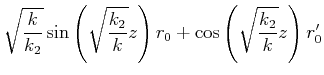 |
(6..25) |
Aus der Elektrizitätslehre folgt (ohne Ableitung), dass für das elektrische Feld
| (6..26) |
gilt. Wir beschränken uns auf den Fall wo
![]() gilt.
Der Laplace-Operator in Zylinderkoordinaten für Funktionen, die nur von
gilt.
Der Laplace-Operator in Zylinderkoordinaten für Funktionen, die nur von
![]() abhängen, ist
abhängen, ist
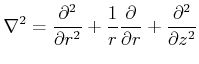 |
(6..27) |
Wir verwenden die Abkürzung
![]() . Weiter setzen wir an:
. Weiter setzen wir an:
| (6..28) |
und erhalten
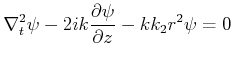 |
(6..29) |
Wenn die Intensität entlang ![]() sich nur wenig ändert
sich nur wenig ändert
![]() , ist, können wir für
, ist, können wir für ![]() ansetzen
ansetzen
![$\displaystyle \psi(x,y,z) = \exp\left\{-i\left[P(z)+\frac{1}{2}Q(z)r^2\right]\right\}$](img1302.gif) |
(6..30) |
Wir setzen dies ein und bekommen
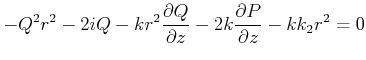 |
(6..31) |
Da dies Gleichung für alle ![]() gelten soll, müssen die Koeffizienten der
verschiedenen Potenzen von
gelten soll, müssen die Koeffizienten der
verschiedenen Potenzen von ![]() einzeln verschwinden. Also ist
einzeln verschwinden. Also ist
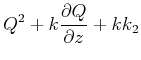 |
|||
| (6..32) |
In einem homogenen Medium ist ![]() so dass wir die Gleichung
so dass wir die Gleichung
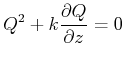 |
(6..33) |
erhalten. Wir definieren die Funktion ![]() über
über
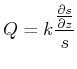 |
(6..34) |
Durch Einsetzen sehen wir, dass
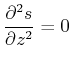 |
(6..35) |
Damit muss
![]() sein. Somit ist
sein. Somit ist ![]()
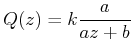 |
(6..36) |
Bequemer ist es im weiteren, wenn wir die Funktion
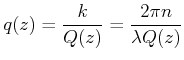 |
(6..37) |
verwenden. Diese hat die Form
| (6..38) |
Wir setzen ![]() in die Gleichung für
in die Gleichung für ![]() ein und erhalten
ein und erhalten
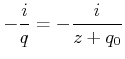 |
|||
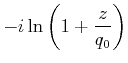 |
(6..39) |
Wir nehmen an, dass ![]() rein imaginär ist. Dann gilt für die örtliche
Amplitudenverteilung
rein imaginär ist. Dann gilt für die örtliche
Amplitudenverteilung
![$\displaystyle \psi(r,z) = exp\left\{-i\left[-i\ln\left(1+\frac{z}{q_0}\right)+\frac{k}{2(q_0+z)}r^2\right]\right\}$](img1323.gif) |
(6..40) |
Wir setzen
![]() , berücksichtigen
, berücksichtigen
![]() und verwenden die Identität
und verwenden die Identität
![]() und erhalten für den ersten Term im obigen
Produkt
und erhalten für den ersten Term im obigen
Produkt
![$\displaystyle \exp\left[-\ln\left(1-i\frac{\lambda z}{\pi\omega_0^2 n}\right)\r...
...^4 n^2}}}\exp\left[i\arctan\left(\frac{\lambda z}{\pi \omega_0 n}\right)\right]$](img1327.gif) |
(6..41) |
Der zweite Term wird
![$\displaystyle \exp\left[\frac{-ikr^2}{2(q_0+z)}\right] = \exp\left\{\frac{-r^2}...
...ikr^2}{2z\left[1+\left(\frac{\pi\omega_0 n}{\lambda z}\right)^2\right]}\right\}$](img1328.gif) |
(6..42) |
Die folgenden Definitionen sind üblich
![$\displaystyle \omega_0^2\left[1+\left(\frac{\lambda z}{\pi \omega_0^2 n}\right)^2\right]=\omega_0^2\left(1+\frac{z^2}{z_0^2}\right)$](img1330.gif) |
(6..43) | ||
![$\displaystyle \left[1+\left(\frac{\pi\omega_0 n}{\lambda z}\right)^2\right] = z\left(1+\frac{z_0^2}{z^2}\right)$](img1332.gif) |
(6..44) | ||
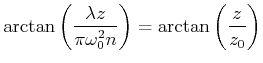 |
(6..45) | ||
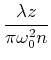 |
(6..46) |
Die Parameter haben die folgende Bedeutung:
| Der halbe Strahldurchmesser an der Position |
|
| Der Krümmungsradius der Wellenfront an der Stelle |
|
| Phasenfaktor | |
| Ort der maximalen Krümmung der Wellenfront |
Mit dieser abgekürzten Schreibweise wird
![$\displaystyle E(x,y,z) = E-0 \frac{\omega_0}{\omega(z)}\exp\left[-i\left(kz-\eta(z)\right)-r^2\left(\frac{1}{\omega^2(z)}+\frac{ik}{2r(z)}\right)\right]$](img1340.gif) |
(6..47) |
Weiter ist
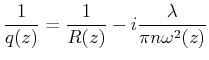 |
(6..48) |
Die Grösse ![]() beschreibt die Gaussschen Strahlen. Der Realteil gibt den
Krümmungsradius der Wellenfronten, der Imaginärteil den Strahldurchmesser.
beschreibt die Gaussschen Strahlen. Der Realteil gibt den
Krümmungsradius der Wellenfronten, der Imaginärteil den Strahldurchmesser.
|
Die Grösse |
(Siehe Yariv, Quantum Electronics [Yar75, pp. 106])
Die obigen Parameter haben die folgende Bedeutung
Die transversale Amplitudenverteilung folgt einer Gausskurve, wie man aus dem
Term
![]() ersehen kann.
ersehen kann. ![]() ist die Distanz zur
optischen Achse, bei der die Intensität um den Faktor
ist die Distanz zur
optischen Achse, bei der die Intensität um den Faktor ![]() vom Maximum
abgefallen ist.
vom Maximum
abgefallen ist. ![]() beschreibt den minimalen Strahldurchmesser.
beschreibt den minimalen Strahldurchmesser.
![]() ist der Krümmungsradius der Wellenfronten. Aus
ist der Krümmungsradius der Wellenfronten. Aus
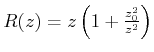 ist ersichtlich, dass
ist ersichtlich, dass
![]() ist. Damit nähern Gausssche Wellen
im Fokus eine ebene Welle an. Ebenso ist
ist. Damit nähern Gausssche Wellen
im Fokus eine ebene Welle an. Ebenso ist
![]() . Auch für sehr grosse Distanzen sind Gausssche wellen eine
gute Approximation für ebene Wellen.
. Auch für sehr grosse Distanzen sind Gausssche wellen eine
gute Approximation für ebene Wellen.
Weit weg vom minimalen Strahldurchmesser kann ein Gaussscher Strahl durch einen Öffnungswinkel
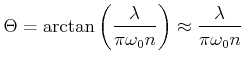 |
(6..49) |
beschrieben werden. Es gilt deshalb die folgende Gleichung
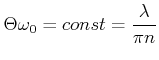 |
(6..50) |
die formal äquivalent zur Unschärferelation ist. Damit ist klar, dass ein
kleinerer Brennfleck unweigerlich einen grösseren Öffnungswinkel bedeutet. In
einer nullten Approximation sieht man auch, dass
![]() sein muss.
sein muss.
Die Transformation eines Gaussschen Strahls mit optischen Elementen, die durch die Matrix
![$\displaystyle \left[\begin{array}{cc} A & B C & D \end{array}\right]$](img1352.gif) |
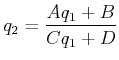 |
(6..51) |
beschrieben. Zum Beispiel wirkt eine Linse mit der Brennweite
![]() , also der Matrix
, also der Matrix
![$\displaystyle \left[\begin{array}{cc} 1 & 0 -1/f & 1 \end{array}\right]$](img1355.gif) |
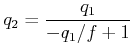 |
(6..52) |
Wir nehmen den Kehrwert und bekommen
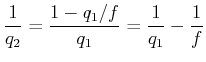 |
(6..53) |
Mit der Definition
![]() wird die Gleichung
wird die Gleichung
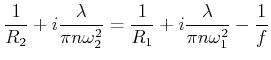 |
(6..54) |
Diese Gleichung muss für den Real- und den Imaginärteil separat erfüllt sein. Also haben wir
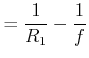 |
|||
| (6..55) |
Wenn zwei optische Elemente mit den Matrizen
![$\displaystyle \left[\begin{array}{cc} A_1 & B_1 C_1 & D_1 \end{array}\right]$](img1366.gif) |
und
![$\displaystyle \left[\begin{array}{cc} A_2 & B_2 C_2 & D_2 \end{array}\right]$](img1367.gif) |
hintereinander geschaltet, ist das Resultat durch
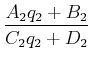 |
|||
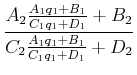 |
|||
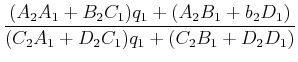 |
|||
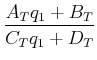 |
(6..56) |
gegeben. Die Analyse dieser Gleichung zeigt, dass für die Koeffizienten auch
![$\displaystyle \left[\begin{array}{cc} A_T & B_T C_T & D_T \end{array}\right...
...array}\right]\left[\begin{array}{cc} A_1 & B_1 C_1 & D_1 \end{array}\right]$](img1373.gif) |
(6..57) |
gilt. Damit gelten für Gausssche Strahlen die gleichen mathematischen Formeln für die Berechnung von optischen Systemen wie bei Lichtstrahlen.
![\includegraphics[width=0.8\textwidth]{gauss-linse}](img1374.gif)
Fokussierung eines Gaussschen Strahls.
|
In der Eingangsebene ![]() ist
ist
![]() und
und
![]() . Dann
ist
. Dann
ist
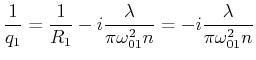 |
(6..58) |
In der Ebene ![]() ist
ist
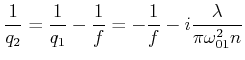 |
(6..59) |
Damit ist
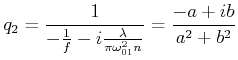 |
(6..60) |
wobei ![]() und
und
![]() . In der Ebene
. In der Ebene ![]() ist
ist
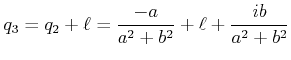 |
(6..61) |
Nun muss in der Ebene ![]() auch gelten
auch gelten
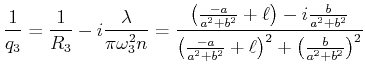 |
(6..62) |
In der Ebene ![]() soll der Durchmesser minimal sein, also ist
soll der Durchmesser minimal sein, also ist
![]() .
Damit muss in der obigen Gleichung der Realteil null sein. Damit ergibt sich
die Bedingung
.
Damit muss in der obigen Gleichung der Realteil null sein. Damit ergibt sich
die Bedingung
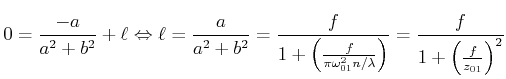 |
(6..63) |
Und damit ist auch der Ort des Strahlminimums gegeben. Der neue Strahldurchmesser ist
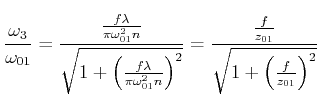 |
(6..64) |
Der Parameter ![]() ist der konfokale Parameter, der angibt, in welcher Distanz
vom Strahlminimum der Strahldurchmesser um
ist der konfokale Parameter, der angibt, in welcher Distanz
vom Strahlminimum der Strahldurchmesser um ![]() zunimmt. Der Wert des
konfokalen Parameters ist
zunimmt. Der Wert des
konfokalen Parameters ist
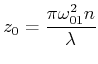 |
(6..65) |
(Siehe Hecht, Optik [Hec, pp. 881]) (Siehe Yariv, Quantum Electronics [Yar75, pp. 118])
|
|
Die Gaussschen Strahlen sind die Grundmode von Laserstrahlung. Sie zeichnen sich dadurch aus, dass sie keine Knotenlinie hat. Es existieren weiter Moden, die durch die Anzahl Knotenlinien in horizontaler und vertikaler Richtung charakterisiert sind. Die möglichen Moden sind durch die Randbedingungen vorgegeben. So erzeugt eine vertikale Störung durch die Resonatorachse eine Mode mit zwei Maxima, die durch eine vertikale Knotenlinie getrennt sind.
Im folgenden werden Messungen von Moden gezeigt, die im Institut für Experimentelle Physik an vertikal emittierenden Laserdioden (VCSEL) aus der Abteilung Optoelektronik gemessen wurden.
![\includegraphics[width=0.8\textwidth]{vcsel-AUFBAU}](img1389.gif)
Aufbau der Nahfeld-Messeinrichtung für Modenverteilungen. (Zeichnung von Markus Fischer[Fis97]).
|
![\includegraphics[width=0.99\textwidth]{vcsel-SPITZEN2}](img1390.gif)
Nahaufnahme von Glasfaser-Nahfeldsonden. (Daten gemessen von Markus Fischer[Fis97]).
|
![\includegraphics[width=0.99\textwidth]{vcsel-SPITZEN1}](img1391.gif)
Transmission von Nahfeld-Glasfasersonden. (Schaubild gezeichnet von Markus Fischer[Fis97]).
|
![\includegraphics[width=0.99\textwidth]{vcsel-ELLIP-0}](img1392.gif)
![\includegraphics[width=0.99\textwidth]{vcsel-ELLIP}](img1393.gif)
Wellenleitermoden für elliptische
Wellenleiter. Links sind die Bezeichnungen, dann die Anordnung der elektrischen Felder und schliesslich die Intensitätsmuster gezeigt. (gezeichnet nach [Dyo95].)
|
![\includegraphics[width=0.8\textwidth]{vcsel-ME_II_2}](img1394.gif)
Diese Aufnahme zeigt Moden bei relativ geringen Strömen. Deshalb können nur die Grundmode sowie noch wenige Oberwellen anschwingen. Die Modenform wird durch die Verunreinigungen auf den Laserspiegeln (rechts sichtbar) hervorgerufen. In der Unteren Reihe ist der Analysator für die Polarisation um
|
![\includegraphics[width=0.99\textwidth]{vcsel-ME_III_2}](img1395.gif)
Bei ähnlichem Strom hängen die möglichen Moden auch vom Durchmesser des Resonators ab. Dieser Resonator ist grösser als der im vorherigen Bild. (Daten gemessen von Markus Fischer[Fis97]).
|
![\includegraphics[width=0.99\textwidth]{vcsel-ME_III_3}](img1396.gif)
![\includegraphics[width=0.99\textwidth]{vcsel-ME_III_4}](img1397.gif)
Hier ist der Strom bei gleicher Geometrie grösser als im vorherigen Bild. Entsprechend schwingen mehr Moden an. Beachten Sie, dass die Knotenlinien von Moden mit einer orthogonalen Polarisation auch orthogonal sind. (Daten gemessen von Markus Fischer[Fis97]).
|
![\includegraphics[width=0.99\textwidth]{vcsel-ME_V_4}](img1398.gif)
![\includegraphics[width=0.99\textwidth]{vcsel-ME_V_5}](img1399.gif)
Dieser Laserresonator hat den grösseren Durchmesser als der vorherige. Da auch der Injektionsstrom grösser ist, schwingen hier sehr viele Moden an, die zum Teil auch nicht mehr identifiziert werden können. (Daten gemessen von Markus Fischer[Fis97]).
|
![\includegraphics[width=0.99\textwidth]{vcsel-POLVER1}](img1400.gif)
Hier wird gezeigt, dass die Sonde, hier ''Spitze'' genannt, keinen Einfluss auf die Messung hat. (Daten gemessen von Markus Fischer[Fis97]).
|
![\includegraphics[width=0.99\textwidth]{vcsel-STREIFEN}](img1401.gif)
Wie bei allen Messmethoden gibt es auch hier Artefakte. So führen hier Rückwirkungen auf den Laser zu einer optisch sonst nicht erklärbaren Streifenbildung. (Daten gemessen von Markus Fischer[Fis97]).
|
Nach Yariv[Yar75, 118] genügen die Moden in rechteckförmigen Wellenleiter
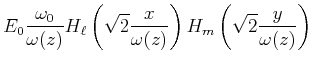 |
|||
![$\displaystyle \times \exp\left[-ik\frac{x^2+y^2}{2q(z)}-ikz+i(m+n+1)\eta\right]$](img1404.gif) |
|||
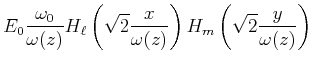 |
|||
![$\displaystyle \times \exp\left[-\frac{x^2+y^2}{\omega^2(z)}-ik\frac{x^2+y^2}{2R(z)}-ikz+i(m+n+1)\eta\right]$](img1405.gif) |
wobei ![]() das Hermitsche Polynom
das Hermitsche Polynom ![]() -ten Grades ist und die anderen
Grössen wie bei den Gaussschen Strahlen definiert sind.
-ten Grades ist und die anderen
Grössen wie bei den Gaussschen Strahlen definiert sind.
Othmar Marti