Die Arbeit ist durch
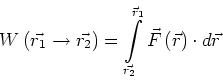 |
(2.32) |
definiert.
Die potentielle Energie eines Kraftfeldes
![]() ist die Arbeit gegen diese
Feldkraft. Nach dem 3. Newtonschen Axiom ist
ist die Arbeit gegen diese
Feldkraft. Nach dem 3. Newtonschen Axiom ist
![]() . Also
. Also
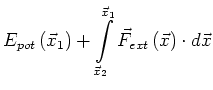 |
(2.33) | ||
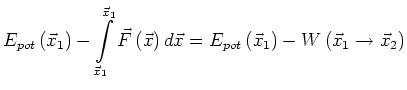 |
(2.34) |
Eine potentielle Energie existiert, wenn
Die potentielle Energie einer Probeladung ![]() im Feld der Ladung
im Feld der Ladung ![]() ist
ist
![\includegraphics[width=0.99\textwidth]{elektrostatik-030.eps}](img178.gif)
|
Da wir jede Bahnkurve durch Stücke in radialer Richtung und durch Bahnen mit
![]() approximieren
können, und da die Bahnen auf den Kugelflächen keinen Beitrag geben (sie sind senkrecht zur
Kraft) können wir das Integral vereinfachen.
approximieren
können, und da die Bahnen auf den Kugelflächen keinen Beitrag geben (sie sind senkrecht zur
Kraft) können wir das Integral vereinfachen.
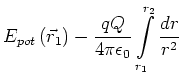 |
(2.36) | ||
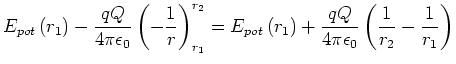 |
(2.37) |
Üblicherweise setzt man
![]() Damit wird
Damit wird
| (2.38) |
Aus der potentiellen Energie kann die Kraft mit dem Gradienten
| (2.39) |
berechnet werden. Für die potentielle Energie der Coulomb-Kraft bekommen
wir
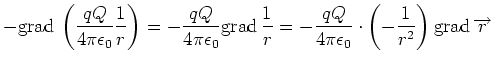 |
|||
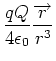 |
(2.40) |
In Komponenten ist
![]() und
und
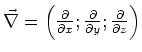
Also
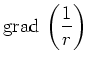 |
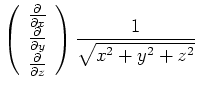 |
||
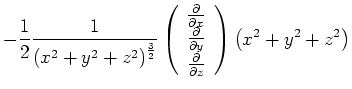 |
|||
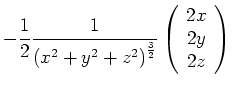 |
|||
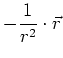 |
(2.41) |
Ergänzend zu Coulomb-Kraft hatten wir das elektrische Feld als auf eine
Einheitsladung normierte Grösse eingeführt.
| (2.42) |
Die potentielle Energie der Ladung ![]() im Feld der Ladung
im Feld der Ladung ![]() , normiert auf
, normiert auf ![]() ist das
elektrische Potential
ist das
elektrische Potential ![]() , auch
Spannung
, auch
Spannung ![]() genannt. Ich verwende in diesem Skript die Begriffe elektrisches Potential und
Spannung austauschbar.
genannt. Ich verwende in diesem Skript die Begriffe elektrisches Potential und
Spannung austauschbar.
Wichtig ist die Beziehung
| (2.44) |
Wie die Kraft aus der potentiellen Energie über die Gradientenbildung hervorgeht, wird das elektrische Feld mit
| (2.45) |
berechnet.
Folgende Relationen gelten
Wir merken uns
analog zur potentiellen Energie.
Die Einheit des elektrostatischen Potentials oder der Spannung ist
Bem.: Beim elektrischen Feld ist der Feldvektor ![]() , bei der Gravitation
, bei der Gravitation ![]()
Das Gravitationspotential ist
![]() .
.
Da die Coulomb-Kräfte additiv sind, ist auch das elektrostatische Potential oder die elektrostatische
potentielle Energie additiv. Das Potential von Ladungen ![]() an den Orten
an den Orten ![]() ist also
ist also
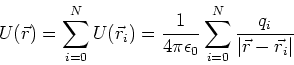 |
(2.47) |
Für kontinuierliche Ladungsverteilungen ![]() ist das Potential
ist das Potential
Versuch zur Vorlesung: Flächenladungsdichte ES-8
Das elektrostatische Potential eines Kreisringes mit der Ladung ![]() und dem Radius
und dem Radius ![]() im Abstand
im Abstand ![]() auf der
Symmetrieachse ist
auf der
Symmetrieachse ist
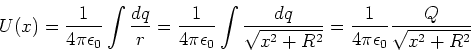 |
(2.49) |
![\includegraphics[width=0.7\textwidth]{kreisringpot.eps}](img218.gif)
Potential eines Kreisringes entlang der Symmetrieachse
|
Analog kann das Potential einer homogen geladenen Scheibe mit dem Radius ![]() entlang ihrer Symmetrieachse
entlang ihrer Symmetrieachse ![]() berechnet werden. Die Ladungsdichte der Scheibe sei
berechnet werden. Die Ladungsdichte der Scheibe sei
![]() . Ein Kreisring mit dem Radius
. Ein Kreisring mit dem Radius ![]() trägt die Ladung
trägt die Ladung
![]() und erzeugt dann das Potential
und erzeugt dann das Potential
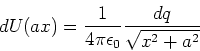 |
(2.50) |
Durch Integration über die gesamte Scheibe erhalten wir
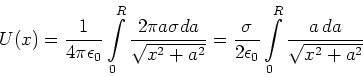 |
(2.51) |
Dieses Integral ergibt nach Bronstein[BSMM00, Seite 309, Nr. 193]
| (2.52) |
![\includegraphics[width=0.7\textwidth]{kreispot.eps}](img224.gif)
Elektrostatisches Potential einer homogen geladenen Kreisscheibe entlang ihrer Symmetrieachse
|
Eine homogen mit der Flächenladungsdichte ![]() geladene Ebene erzeugt ein konstantes elektrisches Feld
geladene Ebene erzeugt ein konstantes elektrisches Feld
![]() . Das elektrostatische Potential eines Punktes
. Das elektrostatische Potential eines Punktes ![]() im Abstand
im Abstand ![]() von der Platte
kann gefunden werden, indem wir entlang des Lots vom Punkt
von der Platte
kann gefunden werden, indem wir entlang des Lots vom Punkt ![]() auf die Ebene integrieren.
auf die Ebene integrieren.
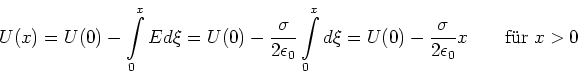 |
(2.53) |
Für ![]() berechnet man
berechnet man
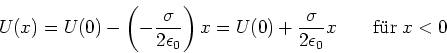 |
(2.54) |
![\includegraphics[width=0.7\textwidth]{ebenepot.eps}](img231.gif)
Potential senkrecht zu einer homogen geladenen Ebene
|
Das Potential einer homogen geladenen Kugelschale wird mit dem elektrischen Feld berechnet. Das radiale
elektrische Feld ist
![]() . Damit ist das Potential
. Damit ist das Potential
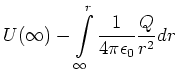 |
|||
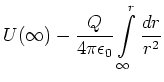 |
|||
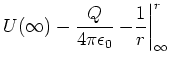 |
|||
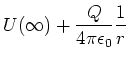 |
(2.55) |
Oder mit ![]()
| (2.56) |
Innerhalb der Kugelschale ist das elektrische Feld null, das Potential also konstant.
| (2.57) |
![\includegraphics[width=0.7\textwidth]{kugelschalepot.eps}](img241.gif)
Potential einer homogen geladenen Kugelschale
|
Schliesslich berechnen wir das elektrostatische Potential in der Nähe einer unendlich ausgedehnten
Linienladung mit der Ladungsdichte ![]() . Das radiale elektrische Feld ist
. Das radiale elektrische Feld ist
![]() . Das Potential ist dann
. Das Potential ist dann
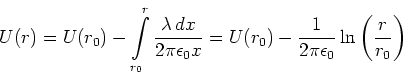 |
(2.58) |
Wir setzen ![]() und erhalten
und erhalten
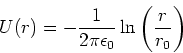 |
(2.59) |
![\includegraphics[width=0.7\textwidth]{linienpot.eps}](img247.gif)
Potential in der Nähe einer unendlich ausgedehnten homogenen Linienladung
|