Wir hatten in Gleichung (2.19) gesehen, dass
ist.
Gleichung (2.52) besagt, dass
| (2.61) |
ist. Mit der im Vakuum geltenden Beziehung
![]() erhalten wir die Poisson-Gleichung.
erhalten wir die Poisson-Gleichung.
| (2.62) |
oder
Dabei haben wir den Laplace-Operator
![]() verwendet. In Komponentenschreibweise in
einem
kartesischen Koordinatensystem ist dies
verwendet. In Komponentenschreibweise in
einem
kartesischen Koordinatensystem ist dies
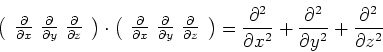 |
(2.64) |
Die Poissongleichung ermöglicht eine Berechnung der Potentiale ausgehend von Ladungsverteilungen.
Beispiel:
Bei einer geladenen Ebene ist
![]() .
Die Poissongleichung wird, wegen der Translationssymmetrie in
.
Die Poissongleichung wird, wegen der Translationssymmetrie in ![]() und
und ![]() zu
zu
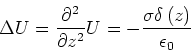 |
(2.65) |
Daraus folgt, dass
![]() für
für ![]() .
.
Bei ![]() haben wir einen Sprung der Grösse
haben wir einen Sprung der Grösse
![]() der symmetrisch von
der symmetrisch von
![]() bis
bis
![]() reichen muss. Nochmals
integrieren ergibt
reichen muss. Nochmals
integrieren ergibt
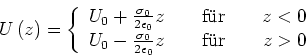 |
(2.66) |
![]() ist eine frei wählbare Integrationskonstante.
ist eine frei wählbare Integrationskonstante.
Das Innere eines Leiters ist ein Äquipotentialraum, da in einem Leiter Ladungen sich frei bewegen können. Da
Feldlinien ![]() senkrecht zu einer Metalloberfläche, die immer eine Äquipotentialfläche ist, stehen
kann man schliessen (und mathematisch beweisen), dass Feldlinien senkrecht auf Äquipotentialflächen stehen.
senkrecht zu einer Metalloberfläche, die immer eine Äquipotentialfläche ist, stehen
kann man schliessen (und mathematisch beweisen), dass Feldlinien senkrecht auf Äquipotentialflächen stehen.
Die möglichen Potentialdifferenzen werden durch Funkenüberschläge begrenzt. Für Luft unter Normalbedingungen
muß
| (2.67) |
sein.