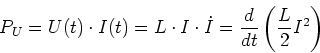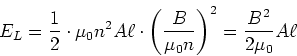



Next: Magnetische Eigenschaften der Materie
Up: Elektrodynamik: zeitlich veränderliche Magnetfelder
Previous: Das Faradaysche Induktionsgesetz
|
Berechnung der Energie im Magnetfeld
|
Wir betrachten eine mit einer Wechselstromquelle
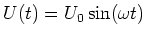 verbundene reale Spule. Diese
Spule wird modelliert durch einen Widerstand
verbundene reale Spule. Diese
Spule wird modelliert durch einen Widerstand 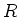 und eine ideale Spule
und eine ideale Spule 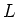 . Die Differentialgleichung dieses
Kreises lautet
. Die Differentialgleichung dieses
Kreises lautet
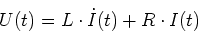 |
(4.91) |
Die stationäre Lösung dieser Gleichung hat die Form
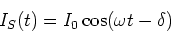 |
(4.92) |
Für den Fall, dass
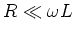 ist, bekommt man
ist, bekommt man
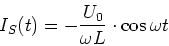 |
(4.93) |
Die momentane Leistung der Spannungsquelle ist
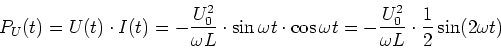 |
(4.94) |
Die Leistung der Spannungsquelle kann nur die Energie des 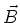 -Feldes ändern, da wir keine dissipativen
Elemente haben (
-Feldes ändern, da wir keine dissipativen
Elemente haben (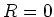 ). Wenn man die Differentialgleichung für den Fall mit
). Wenn man die Differentialgleichung für den Fall mit 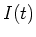 multipliziert, bekommt man
multipliziert, bekommt man
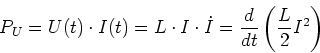 |
(4.95) |
Nun ist aber 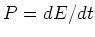 . Damit ist die Energie des Magnetfeldes
. Damit ist die Energie des Magnetfeldes
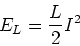 |
(4.96) |
Um die Energiedichte eines Magnetfeldes zu berechnen betrachten wir eine Spule
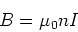 |
(4.97) |
mit der Selbstinduktivität
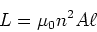 |
(4.98) |
wobei 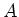 der Querschnitt der Spule und
der Querschnitt der Spule und 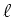 ihre Länge ist. Eingesetzt in die Gleichung für die Energie
ihre Länge ist. Eingesetzt in die Gleichung für die Energie
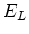 bekommt man
bekommt man
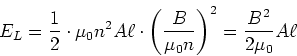 |
(4.99) |
Deshalb ist die Energiedichte des 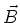 -Feldes
-Feldes
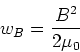 |
(4.100) |




Next: Magnetische Eigenschaften der Materie
Up: Elektrodynamik: zeitlich veränderliche Magnetfelder
Previous: Das Faradaysche Induktionsgesetz
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.4\textwidth]{magnetismus-018.eps}](img1112.gif)
![]() verbundene reale Spule. Diese
Spule wird modelliert durch einen Widerstand
verbundene reale Spule. Diese
Spule wird modelliert durch einen Widerstand ![]() und eine ideale Spule
und eine ideale Spule ![]() . Die Differentialgleichung dieses
Kreises lautet
. Die Differentialgleichung dieses
Kreises lautet