![\includegraphics[width=0.5\textwidth]{strom-017.eps}](img928.gif)
|
Wir bewegen eine Leiterschlaufe mit der Geschwindigkeit ![]() aus dem begrenzten Gebiet mit einem
homogenen Magnetfeld heraus. Auf die beweglichen Ladungsträger, hier positiv angenommen, wirkt die
Lorentzkraft
aus dem begrenzten Gebiet mit einem
homogenen Magnetfeld heraus. Auf die beweglichen Ladungsträger, hier positiv angenommen, wirkt die
Lorentzkraft ![]() . Auf den horizontalen Teilen der Leiterschlaufe kennen wir den Effekt: eine
Hallspannung auf. Im vertikalen Teil im Magnetfeld bewirkt die Hallspannung eine
Beschleunigung der Ladungsträger. Nach der Definition der elektromotorischen Kraft
haben wir
. Auf den horizontalen Teilen der Leiterschlaufe kennen wir den Effekt: eine
Hallspannung auf. Im vertikalen Teil im Magnetfeld bewirkt die Hallspannung eine
Beschleunigung der Ladungsträger. Nach der Definition der elektromotorischen Kraft
haben wir
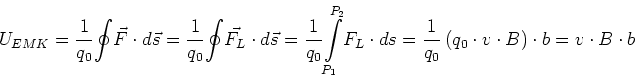 |
(4.2) |
| (4.3) |
Versuch zur Vorlesung: Induktion EM025
Versuch zur Vorlesung: Induktion im Erdfeld EM027
Im Zusammenhang mit den elektrischen Feldern ![]() hatten wir den elektrischen Fluss
hatten wir den elektrischen Fluss
![]() eingeführt. Hier bewegen wir die Leiterschlaufe mit der Geschwindigkeit
eingeführt. Hier bewegen wir die Leiterschlaufe mit der Geschwindigkeit ![]() , wir
ändern damit die vom Magnetfeld durchflossene Fläche um die Grösse
, wir
ändern damit die vom Magnetfeld durchflossene Fläche um die Grösse
![]() . Da die
Geschwindigkeit
. Da die
Geschwindigkeit ![]() ist, können wir auch schreiben
ist, können wir auch schreiben
| (4.4) |
Damit ist die induzierte EMK
Die Einheit des magnetischen Flusses ist Weber.
| (4.6) |
Das Minuszeichen in den Gleichungen für den magnetischen Fluss rührt daher, dass eine Geschwindigkeit in die
positive ![]() -Richtung eine Verkleinerung der Fläche
-Richtung eine Verkleinerung der Fläche ![]() bewirkt. Das durch den Strom erzeugte Magnetfeld ist
so gerichtet, dass die Bewegung der Spule gebremst wird. Dieses Verhalten wird in der Lenzschen
Regel zusammengefasst:
bewirkt. Das durch den Strom erzeugte Magnetfeld ist
so gerichtet, dass die Bewegung der Spule gebremst wird. Dieses Verhalten wird in der Lenzschen
Regel zusammengefasst:
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{
D...
...t, sind stets so gerichtet, dass sie der Ursache
entgegenwirken.}\end{minipage}}](img938.gif)
![\includegraphics[width=0.6\textwidth]{magnetismus-002.eps}](img939.gif)
|
Eine Spule erzeugt ein axiales Magnetfeld. Die Richtung des Magnetfeldes wird mit der Rechten Hand-Regel aus der Stromrichtung abgeleitet. Ein Stabmagnet erzeugt ein gleiches Magnetfeld wie eine Spule.
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Di...
...t: Die $\vec B$-Feldlinien laufen vom Nordpol zum
S{\uml u}dpol.}\end{minipage}}](img940.gif)
![\includegraphics[width=0.6\textwidth]{magnetismus-003.eps}](img941.gif)
|
Bewegt man einen Magneten mit der Geschwindigkeit ![]() von einem Stabmagneten weg, so bewirkt die
Lorentzkraft einen Strom
von einem Stabmagneten weg, so bewirkt die
Lorentzkraft einen Strom ![]() , der ein Magnetfeld
, der ein Magnetfeld ![]() induziert. Dieses Magnetfeld ist so
gerichtet, dass es gleichsinnig wie das Magnetfeld des Stabes ist. Der Metallring wird also vom Stabmagneten
angezogen und in seiner Bewegung nach rechts gebremst (Lenzsche Regel).
induziert. Dieses Magnetfeld ist so
gerichtet, dass es gleichsinnig wie das Magnetfeld des Stabes ist. Der Metallring wird also vom Stabmagneten
angezogen und in seiner Bewegung nach rechts gebremst (Lenzsche Regel).
![\includegraphics[width=0.9\textwidth]{magnetismus-001.eps}](img943.gif)
|
Hier wird ein Magnetfeld eingeschaltet. Die Richtung der Feldlinien wird durch die Rechte-Hand-Regel bestimmt. Ein zeitlich zunehmendes Magnetfeld in der rechten Spule ist äquivalent zu einer Bewegung der rechten Spule im inhomogenen Feld (links intensiver als rechts) nach links. Dabei zeigt die relevante Feldkomponente nach aussen. Aus der Rechten Hand-Regel ergibt sich die angegebene Stromrichtung. Nach dem Ausschalten des erregenden Stromes nimmt die Intensität des Magnetfeldes ab. Dies ist äquivalent zu einer Bewegung der rechten Spule nach rechts, bei gleichbleibender Richtung des Magnetfeldes. Entsprechend dreht sich die Richtung des Stromes um.
![\includegraphics[width=0.3\textwidth]{magnetismus-004.eps}](img944.gif)
|
Wenn eine Spule von einem Strom durchflossen ist, wird dadurch ein Magnetfeld erzeugt. Wenn nun der Strom durch die Spule geändert wird, wird eine Spannung induziert, die wie im vorigen Falle so gerichtet ist, dass sie der Änderung des Magnetfeldes entgegenwirkt, so also auch der Änderung des durch die Spule fliessenden Stromes. Im besonderen Falle, dass der Strom abgeschaltet wird, dass also der Widerstand im Stromkreis um viele Grössenordnungen steigt, bildet sich eine sehr hohe Spannung.
Anwendungen
Wir betrachten die Situation in der Abbildung im Ruhesystem ![]() der Schleife. Im
Laborsystem
der Schleife. Im
Laborsystem ![]() ist das Magnetfeld
ist das Magnetfeld
| (4.7) | |||
| (4.8) |
| (4.9) |
Die Gleichungen (4.12) gelten in jedem Falle. Wenn ![]() ist, kann man die Unterschiede
im Strom
ist, kann man die Unterschiede
im Strom ![]() , in der EMK
, in der EMK ![]() und im Magnetfeld
und im Magnetfeld ![]() vernachlässigen.
vernachlässigen.
Die Transformationseigenschaften zeigen, dass das Induktionsgesetz auch bei stationären Leiterschleifen und
zeitlich ändernden Magnetfeldern gelten muss (wir begeben uns in das System ![]() ). Die Wirkung der Felder
). Die Wirkung der Felder
![]() und
und ![]() sind unabhängig von ihrer Entstehung.
sind unabhängig von ihrer Entstehung.
Versuch zur Vorlesung: Magnetische Induktion EM051
Für einen beliebig geformten ruhenden Leiter (gegeben durch die Kurve ![]() ) in einem zeitlich ändernden
Magnetfeld gilt für die EMK
) in einem zeitlich ändernden
Magnetfeld gilt für die EMK
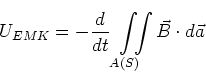 |
(4.12) |
Da der Leiter in Ruhe ist, muss die EMK durch ein elektrisches Feld erzeugt sein.
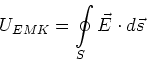 |
(4.13) |
Die beiden Formulierungen müssen äquivalent sein, also erhalten wir das universelle Induktionsgesetz von Faraday
Mit dem Satz von Stokes erhält man
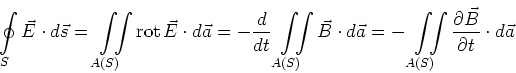 |
(4.14) |
Da diese Integralgleichung für beliebige Kurven ![]() gelten muss, also auch für infinitesimal kleine, erhalten
wir die differentielle Form des Faradayschen Induktionsgesetzes
gelten muss, also auch für infinitesimal kleine, erhalten
wir die differentielle Form des Faradayschen Induktionsgesetzes
Versuch zur Vorlesung: Fallrohre EM057
![\includegraphics[width=0.3\textwidth]{magnetismus-005.eps}](img966.gif)
|
Wenn sich ein Metallstück in einem inhomogenen Magnetfeld befindet, dann muss für jede Bahnkurve ![]() das
Faradaysche Induktionsgesetz gelten. Da der Leiter einen spezifischen Widerstand
das
Faradaysche Induktionsgesetz gelten. Da der Leiter einen spezifischen Widerstand ![]() hat, fliesst bei
einer Änderung des Flusses durch
hat, fliesst bei
einer Änderung des Flusses durch ![]() , zum Beispiel, indem man den Leiter bewegt, ein durch die induzierte
Spannung getriebener Strom. Die Richtung des Stromes ist so, dass er sich einer Änderung des magnetischen
Flusses widersetzt. Bei einem perfekten Leiter, müssten enorm grosse Kräfte aufgebracht werden, um das
Metallstück mit einer minimalen Geschwindigkeit bewegen zu können. Durch die Dissipation im Ohmschen Leiter
wird der induzierte Strom geschwächt, so dass die der Bewegung entgegengesetzte Kraft umso kleiner ist, je
schlechter die Leitfähigkeit des Metalls ist.
, zum Beispiel, indem man den Leiter bewegt, ein durch die induzierte
Spannung getriebener Strom. Die Richtung des Stromes ist so, dass er sich einer Änderung des magnetischen
Flusses widersetzt. Bei einem perfekten Leiter, müssten enorm grosse Kräfte aufgebracht werden, um das
Metallstück mit einer minimalen Geschwindigkeit bewegen zu können. Durch die Dissipation im Ohmschen Leiter
wird der induzierte Strom geschwächt, so dass die der Bewegung entgegengesetzte Kraft umso kleiner ist, je
schlechter die Leitfähigkeit des Metalls ist.
Wirbelströme können vermindert werden, indem das Metall geschlitzt wird oder in Lagen mit Isolatoren dazwischen gebündelt wird.
Anwendungen
Materialien
Übungsblatt 06 vom 16. 01. 2003 (HTML oder PDF)
Folien zur Vorlesung am 16. 01. 2003 (PDF)
Der magnetische Fluss in einer Spule entsteht durch Ströme in dieser Spule selber, oder in anderen Spulen.
Nach dem Gesetz von Laplace oder Biot-Savart ist das Magnetfeld
proportional zum Strom. Somit ist auch der Fluss ![]() proportional zum Strom. Diese Proportionalität wird
mit
proportional zum Strom. Diese Proportionalität wird
mit
| (4.15) |
Die Einheit der Induktivität ist
| (4.19) |
| (4.20) |
Versuch zur Vorlesung: Funkeninduktor EM017
![\includegraphics[width=0.5\textwidth]{magnetismus-006.eps}](img979.gif)
|
Der magnetische Fluss am Punkt ![]() hängt sowohl vom Strom
hängt sowohl vom Strom ![]() wie auch vom Strom
wie auch vom Strom ![]() ab:
ab:
| (4.22) |
| (4.23) |
![\includegraphics[width=0.7\textwidth]{magnetismus-007.eps}](img986.gif)
|
Im allgemeinen ist es schwierig, die Gegeninduktivitäten zu berechnen. Bei zwei ineinander gewickelten
Spulen, einem Beispiel für einen Transformator, gelingt dies. Wir wollen das Beispiel verwenden, um zu
zeigen, dass ![]() ist. Durch die Spule
ist. Durch die Spule ![]() (Länge
(Länge ![]() , Radius
, Radius ![]() , Windungsdichte
, Windungsdichte
![]() ) fliesst der Strom
) fliesst der Strom ![]() , durch die zweite Spule
, durch die zweite Spule ![]() (Länge
(Länge ![]() , Radius
, Radius ![]() , Windungsdichte
, Windungsdichte
![]() ) soll der Strom
) soll der Strom ![]() fliessen. Da wir lange Spulen betrachten, ist das Magnetfeld im
Inneren der Spulen homogen. Also ist
fliessen. Da wir lange Spulen betrachten, ist das Magnetfeld im
Inneren der Spulen homogen. Also ist
| (4.24) |
| (4.25) |
| (4.26) |
| (4.27) |
| (4.28) |
| (4.29) |
![\includegraphics[width=0.5\textwidth]{magnetismus-008.eps}](img1002.gif)
|
Die in einem Transformator induzierte Spannung kann wie folgt berechnet werden. In der Spule ![]() fällt die
Spannung
fällt die
Spannung
| (4.30) |
| (4.31) |
| (4.32) |
Wird der Ausgang des Transformators mit dem Ohmschen Widerstand ![]() belastet, fliesst der Strom
belastet, fliesst der Strom ![]() , der zu
, der zu
![]() in Phase ist. Dieser Strom erzeugt einen magnetischen Fluss
in Phase ist. Dieser Strom erzeugt einen magnetischen Fluss
![]() , der den
ursprünglichen Fluss
, der den
ursprünglichen Fluss ![]() durch die Spule
durch die Spule ![]() schwächt. Da durch beide Spulen der gleiche magnetische
Fluss fliesst, muss auch der Fluss durch die erste Spule geschwächt werden. Da die Spannung durch die
Spannungsquelle
schwächt. Da durch beide Spulen der gleiche magnetische
Fluss fliesst, muss auch der Fluss durch die erste Spule geschwächt werden. Da die Spannung durch die
Spannungsquelle ![]() vorgegeben ist, muss der Strom
vorgegeben ist, muss der Strom ![]() auf der Primärseite zusätzlich fliessen, so dass
auf der Primärseite zusätzlich fliessen, so dass
![]() gilt. Da die Proportionalitätsfaktoren bis auf das Vorzeichen gleich sind, gilt dann
auch
gilt. Da die Proportionalitätsfaktoren bis auf das Vorzeichen gleich sind, gilt dann
auch
Versuch zur Vorlesung: Hochspannungsleitung EM161
Versuch zur Vorlesung: Transformatorenversuche EM066
![\includegraphics[width=0.7\textwidth]{magnetismus-014.eps}](img1013.gif)
|
In einer komplizierten elektrischen Schaltung betrachtet man eine einzelne Masche. Nach der definition der EMK muss eine Probeladung langsam um die Masche herumgeführt werden. Dies führt auf die Maschenregel
wobei die Vorzeichen entsprechend dem Umlaufsinn einzusetzen sind. In unserem Beispiel bedeutet dies:
Die Knotenregel ist ein Ausdruck für die Ladungserhaltung. An jedem Knoten gilt
Mit diesen beiden Regeln sowie der Kenntnis der Charakteristika der Bauelemente kann jede statische oder quasistatische elektronische Schaltung berechnet werden.
In diesem Abschnitt betrachten wir die Wirkung von cosinusförmigen Wechselspannungen
| (4.36) |
![\includegraphics[width=0.3\textwidth]{magnetismus-009.eps}](img1019.gif)
|
Da bei Wechselspannungen a priori keine Stromrichtung vorgegeben ist, definiert man, zum Beispiel wie in der
Abbildung oben, die Stromrichtung zu einem bestimmten Zeitpunkt, hier für ![]() . Zu jedem Zeitpunkt muss die
Spannung im Stromkreis insgesamt null sein. Also ist
. Zu jedem Zeitpunkt muss die
Spannung im Stromkreis insgesamt null sein. Also ist
| (4.37) |
| (4.38) |
| (4.39) |
Die momentane Leistung am Widerstand ist
| (4.40) |
Unter dem Effektivwert der Spannung (des Stromes) versteht man diejenige Gleichspannung, die an einem
Ohmschen Widerstand die gleiche Verlustleistung erzeugt. Also ist für sinusförmige Spannungen
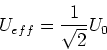 |
(4.42) |
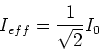 |
(4.43) |
Versuch zur Vorlesung: Wechselstromwiderstand EM053
![\includegraphics[width=0.3\textwidth]{magnetismus-010.eps}](img1033.gif)
|
Wir verwenden Gleichung (4.24) um die Spannung über der Spule zu berechnen. Die induzierte Spannung ist
der Flussänderung entgegengesetzt. Sie wirkt so, dass die Zunahme des Stromes bei zunehmender
Anregungsspannung gebremst wird. Deshalb ist
| (4.46) |
| (4.47) |
| (4.49) |
Die momentan dissipierte Leistung an einer Spule ist
| (4.50) |
| (4.51) |
![\includegraphics[width=0.3\textwidth]{magnetismus-011.eps}](img1044.gif)
|
Beim Kondensator ist ![]() . Diese Spannung muss gleich der treibenden Spannung sein.
. Diese Spannung muss gleich der treibenden Spannung sein.
| (4.52) |
| (4.53) |
| (4.54) |
| (4.56) |
| (4.57) |
| (4.58) |
Versuch zur Vorlesung: Elektrischer
Schwingkreis Em056
![\includegraphics[width=0.3\textwidth]{magnetismus-012.eps}](img1054.gif)
|
Der Kondensator soll zur Zeit ![]() auf die Spannung
auf die Spannung ![]() aufgeladen sein. Zur Zeit
aufgeladen sein. Zur Zeit ![]() wird der
Schalter geschlossen. Die Differentialgleichung dieser Schaltung lautet:
wird der
Schalter geschlossen. Die Differentialgleichung dieser Schaltung lautet:
| (4.59) |
| (4.60) |
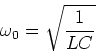 |
(4.61) |
![\includegraphics[width=0.3\textwidth]{magnetismus-013.eps}](img1059.gif)
|
Der gedämpfte Schwingkreis enthält neben dem Kondensator und der Spule auch einen Widerstand. Die
Differentialgleichung des gedämpften Schwingkreises ist
Wenn der elektrische Schwingkreis von einer Wechselspannungsquelle getrieben wird, ergeben sich die gleichen Phänomene wie bei einem getriebenen Pendel, also auch eine Resonanz.
Anwendungen
![\includegraphics[width=0.7\textwidth]{magnetismus-015.eps}](img1063.gif)
|
Versuch zur Vorlesung: Elektromotor und
-generator EM101
Wir betrachten zuerst den Elektromotor als Generator. Der Fluss durch die Leiterschlaufe mit ![]() Windungen
und einer Fläche
Windungen
und einer Fläche ![]() ist
ist
| (4.64) |
| (4.65) |
| (4.66) |
| (4.68) |
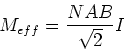 |
(4.69) |
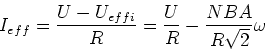 |
(4.70) |
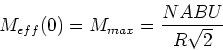 |
(4.72) |
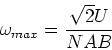 |
(4.73) |
Ist die Erregerwicklung in Serie zur Ankerwicklung geschaltet, gibt es keine maximale Drehzahl. Eine lange
Zylinderspule (Länge ![]() , Windungszahl
, Windungszahl ![]() ) hat das Magnetfeld
) hat das Magnetfeld
| (4.74) |
| (4.75) |
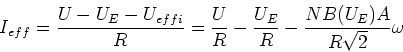 |
(4.76) |
Materialien
Folien zur Vorlesung am 23. 01. 2003 (PDF)
Da ![]() ist, gilt
ist, gilt
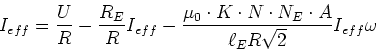 |
(4.77) |
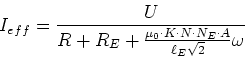 |
(4.78) |
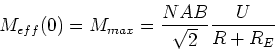 |
(4.80) |
Versuch zur Vorlesung: Linearmotor EM113
Versuch zur Vorlesung: Betatron EM167
Die Idee hinter der Konstruktion des Betatrons ist, dass bei einem zeitabhängigen ![]() -Feld nach
-Feld nach
![]() auch ein zeitabhängiges
auch ein zeitabhängiges ![]() -Feld existiert.
-Feld existiert.
![\includegraphics[width=0.7\textwidth]{magnetismus-016.eps}](img1092.gif)
|
Nach dem Induktionsgesetz
![]() hat das durch ein in die
hat das durch ein in die
![]() -Richtung zeigende Magnetfeld induzierte elektrische Feld keine
-Richtung zeigende Magnetfeld induzierte elektrische Feld keine ![]() -Komponente. Nehmen wir an, dass das
-Komponente. Nehmen wir an, dass das
![]() -Feld eine Radialkomponente hätte. Sie könnte zum Beispiel in die
-Feld eine Radialkomponente hätte. Sie könnte zum Beispiel in die ![]() -Richtung zeigen. Rotieren wir
die ganze Anordnung um
-Richtung zeigen. Rotieren wir
die ganze Anordnung um ![]() um die
um die ![]() -Achse und kehren die Richtung des
-Achse und kehren die Richtung des ![]() -Feldes um, haben wir
wieder die Ausgangsanordnung. Mit der Richtungsumkehr von
-Feldes um, haben wir
wieder die Ausgangsanordnung. Mit der Richtungsumkehr von ![]() hat aber auch
hat aber auch ![]() die Richtung
geändert (Induktionsgesetz). Dies ist aber im Widerspruch zur Ausgangssituation. Deshalb kann es kein
radiales
die Richtung
geändert (Induktionsgesetz). Dies ist aber im Widerspruch zur Ausgangssituation. Deshalb kann es kein
radiales ![]() -Feld geben: das
-Feld geben: das ![]() -Feld ist tangential und beschleunigt die geladenen Teilchen. Damit
die Teilchen auf der Kreisbahn bleiben, muss
-Feld ist tangential und beschleunigt die geladenen Teilchen. Damit
die Teilchen auf der Kreisbahn bleiben, muss
| (4.81) |
| (4.82) |
| (4.83) |
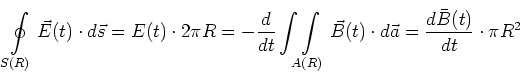 |
(4.84) |
| (4.85) |
| (4.86) |
![\includegraphics[width=0.5\textwidth]{magnetismus-017.eps}](img1104.gif)
|
Bei Gleichstrom in einem zylindrischen Leiter ist das elektrische Feld konstant über dem Querschnitt. Nach dem Ampèreschen Durchflutungsgesetz ist das Magnetfeld proportional zum Abstand.
Für den Fall eines Wechselstroms mit niedriger Frequenz müssen wir das Induktionsgesetz berücksichtigen. Nach
dem Induktionsgesetz gilt für die Kurve ![]() , die auf einer Ebene, in der auch die Zylinderachse liegt, liegt
, die auf einer Ebene, in der auch die Zylinderachse liegt, liegt
| (4.89) |
Anwendung