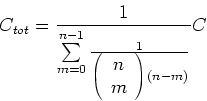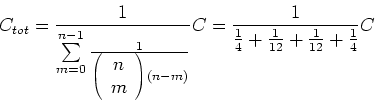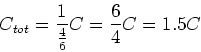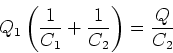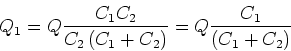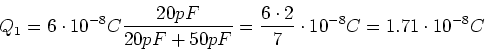

Up: Grundkurs IIIb für Physiker
Übungsblatt 03
Grundkurs IIIb für Physiker
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
18. 11. 2002 oder 25. 11. 2002
Elektrostatisches Potential,
- Zwei identische, ungeladene, metallische Kugeln seien durch einen Draht verbunden (Abbildung a).
Zwei ähnliche leitende Kugeln mit gleich großen, aber entgegengesetzten Ladungen werden in die
Positionen gebracht, die Abbildung b) gezeigt,
- Zeichnen Sie die elektrischen Feldlinien zwischen den Kugeln l und 3 sowie die zwischen den
Kugeln 2 und 4.
- Was kann man über die Potentiale
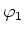 ,
, 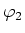 ,
, 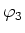 , und
, und 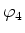 der Kugeln aussagen?
der Kugeln aussagen?
- Zeigen Sie, daß die Endladung auf jeder Kugel null sein muss, wenn man die Kugeln 3 und 4
mit einem Draht verbindet.
- Nach dem Bohrschen Atommodell bewegt sich das Elektron des Wasserstoffatoms auf einer kreisförmigen
Bahn mit dem Radius
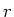 um das Proton,
um das Proton,
- Stellen Sie einen Ausdruck für die kinetische Energie des Elektrons
als Funktion von
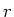 auf, indem Sie die auf das Elektron nach dem Coulomb-Gesetz
einwirkende Kraft gleich
auf, indem Sie die auf das Elektron nach dem Coulomb-Gesetz
einwirkende Kraft gleich 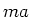 setzen. Hierbei ist
setzen. Hierbei ist 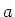 die Zentripetalbeschleunigung.
Zeigen Sie, daß bei jedem Abstand
die Zentripetalbeschleunigung.
Zeigen Sie, daß bei jedem Abstand 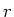 die kinetische
Energie halb so groß ist wie die potentielle Energie,
die kinetische
Energie halb so groß ist wie die potentielle Energie,
- Es sei
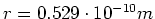 der Radius der
Elektronenbahn im Wasserstoffatom. Berechnen Sie
der Radius der
Elektronenbahn im Wasserstoffatom. Berechnen Sie
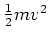 sowie
sowie 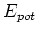 und die Gesamtenergie
und die Gesamtenergie
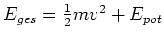 in Elektronenvolt. Die Energie
in Elektronenvolt. Die Energie 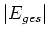 , die nötig ist, um das Elektron aus dem
Wasserstoffatom zu entfernen, heißt lonisierungsenergie.
, die nötig ist, um das Elektron aus dem
Wasserstoffatom zu entfernen, heißt lonisierungsenergie.
- Welche Kapazität hat der Plattenkondensator in der Abbildung?
- Die Platten eines Kondensators haben eine Fläche von
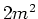 und einen Abstand von
und einen Abstand von 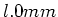 .
Der Kondensator sei auf eine
Spannung von
.
Der Kondensator sei auf eine
Spannung von 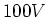 aufgeladen. Wie groß ist
aufgeladen. Wie groß ist
- die elektrische Feldstärke,
- die Energiedichte zwischen den Platten?
- Bestimmen Sie die gespeicherte Energie, indem Sie das Ergebnis von (4b) mit dem
Volumen zwischen den Platten multiplizieren.
- Wie groß ist die Kapazität?
- Berechnen Sie die gespeicherte Energie als
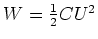 und vergleichen Sie das
Ergebnis mit dem Resultat aus Teil (4c).
und vergleichen Sie das
Ergebnis mit dem Resultat aus Teil (4c).
- (freiwillige Zusatzaufgabe) Berechnen Sie die Ersatzkapazität von
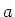 nach
nach 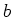 der unten stehenden Schaltung.
der unten stehenden Schaltung.
- Ein
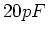 -Kondensator werde auf 3,0 kV aufgeladen, dann von der
Spannungsquelle getrennt und mit einem ungeladenen
-Kondensator werde auf 3,0 kV aufgeladen, dann von der
Spannungsquelle getrennt und mit einem ungeladenen 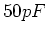 -Kondensator verbunden
-Kondensator verbunden
- Wie verteilen sich die Ladungen?
- Vergleichen Sie die elektrische potentielle Energie in beiden Kondensatoren vor dem
Verbinden mit der nach dem Verbinden.
- Drei Kondensatoren seien, wie in der Abbildung gezeigt, miteinander verbunden. Wie gross ist
die Kapazität zwischen den Punkten
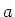 und
und 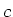 ?
?
- Wie groß ist die Energiedichte in einem
elektrischen Feld, dessen Feldstärke der Durchschlagsfestigkeit von Luft entspricht (
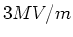 )?
)?

- Berechnen Sie für die Anordnung in der Abbildung mit
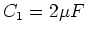 ,
, 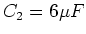 und
und
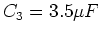 die Ersatzkapazität,
die Ersatzkapazität,
- Die einzelnen Kondensatoren haben eine Durchschlagsfestigkeit
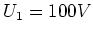 ,
, 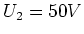 und
und 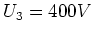 . Welche Spannung kann dann maximal zwischen den Punkten
. Welche Spannung kann dann maximal zwischen den Punkten 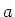 und
und 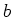 angelegt werden, ohne daß
Durchschläge auftreten?
angelegt werden, ohne daß
Durchschläge auftreten?

- Die Kugeln
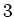 und
und 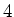 induzieren Ladungen entgegengesetzten Vorzeichens auf den Kugeln
induzieren Ladungen entgegengesetzten Vorzeichens auf den Kugeln 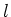 und
und 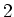 .
Daher haben die Feldlinien folgenden Verlauf:
.
Daher haben die Feldlinien folgenden Verlauf:
- Weil die Kugeln
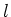 und
und 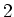 leitend miteinander verbunden sind, haben sie gleiches Potential.
Die positiv geladene Kugel hat das höchste Potential und die negativ geladene das niedrigste Potential.
Also ist
leitend miteinander verbunden sind, haben sie gleiches Potential.
Die positiv geladene Kugel hat das höchste Potential und die negativ geladene das niedrigste Potential.
Also ist
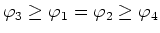 . Die
Gleichheitszeichen gelten, wenn
. Die
Gleichheitszeichen gelten, wenn 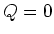 ist. Die Potentiale der Kugeln
ist. Die Potentiale der Kugeln 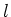 und
und 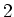 haben
einen mittleren Wert, weil die auf ihnen induzierten Ladungen jeweils nur
einen Bruchteil von
haben
einen mittleren Wert, weil die auf ihnen induzierten Ladungen jeweils nur
einen Bruchteil von 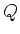 betragen.
betragen.
- Wenn die Kugeln
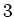 und
und 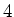 leitend miteinander verbunden werden, dann
haben auch sie gleiches Potential. Wegen
leitend miteinander verbunden werden, dann
haben auch sie gleiches Potential. Wegen
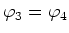 müssen in diesem Falle
alle vier Kugeln gleiches Potential haben. Das ist nur bei
müssen in diesem Falle
alle vier Kugeln gleiches Potential haben. Das ist nur bei 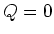 möglich.
möglich.
- Hier ist nach dem zweiten Newtonschen Axiom
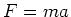 bzw.
bzw.
Daraus folgt
Die potentielle Energie ist
Damit ist
Dies gilt für alle 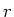 .
.
- Mit
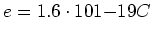 und
und
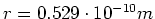 ist die kinetische Energie
ist die kinetische Energie
Damit erhalten wir
und
Also sind 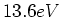 nötig, um ein Wasserstoffatom zu ionisieren.
nötig, um ein Wasserstoffatom zu ionisieren.
- Dieser Kondensator ist eine Kombination von drei Kondensatoren, die jeweils die Fläche
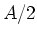 haben.
Die Kondensatoren mit den Dielektrizitätszahlen
haben.
Die Kondensatoren mit den Dielektrizitätszahlen 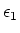 und
und 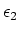 sind in Reihe
geschaltet. Sie haben eine Dicke von
sind in Reihe
geschaltet. Sie haben eine Dicke von 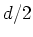 . Parallel dazu ist der Kondensator mit
. Parallel dazu ist der Kondensator mit 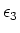 und
der Dicke
und
der Dicke 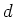 .
.
mit
Zusammen ergibt sich mit
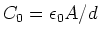
- Sei
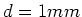 ,
, 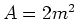 und
und 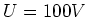
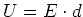 und damit
und damit
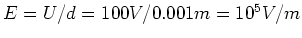
- Die Energiedichte
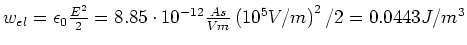
-
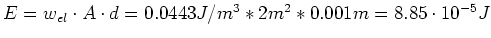
-
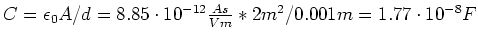
-
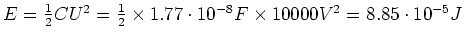
- Die dargestellte Schaltung ist die zweidimensionale Projektion einer vierdimensionalen Schaltung,
bei der jede Kante eines Würfels die gleiche Kapazität trägt. Man nummeriert alle Ecken eines Würfels in
der
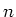 -ten Dimension mit 0 oder 1. Wir erhalten also
-ten Dimension mit 0 oder 1. Wir erhalten also 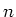 -stellige Zahlen. Zwei Ecken sind miteinander
verbunden, wenn sich die Zahl ihrer Einsen um eins unterscheidet.
-stellige Zahlen. Zwei Ecken sind miteinander
verbunden, wenn sich die Zahl ihrer Einsen um eins unterscheidet.
Wir erhalten die folgende Eckenzahl:
- Alles 0 : 1 Ecke
- Eine 1 : n Ecken
- Zwei 1 :
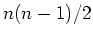 Ecken
Ecken
- Drei 1 :
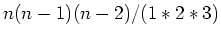 Ecken
Ecken
Allgemein: Es gibt
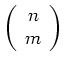 Ecken eines
Ecken eines 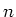 -dimensionalen Würfels mit
-dimensionalen Würfels mit 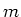 Einsen.
Einsen.
Die zweite Frage, die es zu beantworten gilt, ist: Auf wieviele Arten kann eine 1 hinzugefügt werden?
- Alles 0 : n Arten
- Eine 1 : (n-1) Arten
- Zwei 1 : (n-2) Arten
Allgemein: Wenn 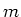 Einsen schon gesetzt sind, kann man auf
Einsen schon gesetzt sind, kann man auf 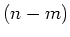 Arten noch eine 1 dazufügen.
Arten noch eine 1 dazufügen.
Nun sind alle Ecken mit der gleichen Anzahl 1 äquivalent bezüglich Symmetrieoperationen um die Achse von
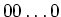 nach
nach 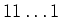 . Sie sind deshalb auf gleichem Potential.
. Sie sind deshalb auf gleichem Potential.
Die Gesamtkapazität ist also die Serieschaltung von
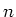 Kapazitäten von der Startecke
Kapazitäten von der Startecke 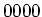 aus
aus
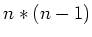 Kapazitäten von Ecken mit einer 1
Kapazitäten von Ecken mit einer 1
-
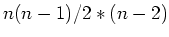 Kapazitäten von Ecken mit zwei 1
Kapazitäten von Ecken mit zwei 1
Allgemein:
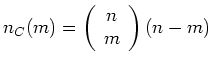 Kapazitäten.
Kapazitäten.
Das Resultat ist also
oder
In unserem Falle haben wir
Bemerkung: Dieses Verfahren lässt sich auch auf Widerstände und Spulen anwenden.
- Mit
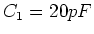 und
und 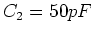
- Ladung auf
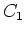 :
:
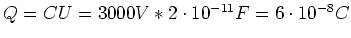
Wenn die beiden Kondensatoren verbunden werden, bleibt 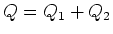 erhalten.
erhalten.
Die neue Spannung muss an beiden gleich sein.
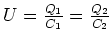
also
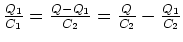
oder
- Die Energie vorher ist
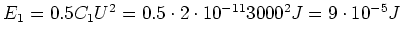
Die Spannung nachher ist
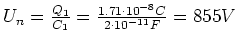
Die Energie nachher ist
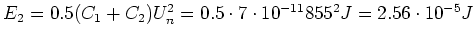
Wo ist die Energie hin? Sie ist in Form von Strahlung und Joulscher Wärme in den Verbindungsdrähten
dissipiert.
-
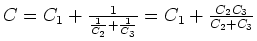
- Wenn wir in der vorherigen Aufgabe
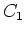 mit
mit 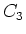 ersetzen, erhalten wir das Resultat für diese
Aufgabe.
ersetzen, erhalten wir das Resultat für diese
Aufgabe.
-
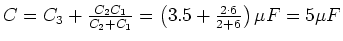
- An
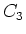 liegt die gesamte Spannung
liegt die gesamte Spannung 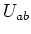 Also ist
Also ist 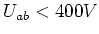
Die Ladung der beiden Kondensatoren ist gleich, also teilt sich die Spannung 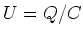 proportional
zu den Kehrwerten der Kondensatoren auf. Die Kapazität der Serieschaltung ist
proportional
zu den Kehrwerten der Kondensatoren auf. Die Kapazität der Serieschaltung ist
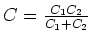
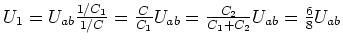
Also
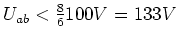
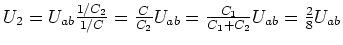
Also
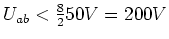
Die maximale Spannung ist 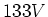 . Das schwächste Bauteil in der Schaltung ist
. Das schwächste Bauteil in der Schaltung ist 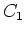 .
.
Übungsblatt 03
Grundkurs IIIb für Physiker
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt03
The translation was initiated by marti on 2002-11-25


Up: Grundkurs IIIb für Physiker
Othmar Marti
Experimentelle Physik
Universiät Ulm
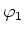 ,
, 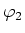 ,
, 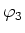 , und
, und 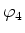 der Kugeln aussagen?
der Kugeln aussagen?
![\includegraphics[width=0.4\textwidth]{ue-03-01.eps}](img5.gif)
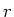 auf, indem Sie die auf das Elektron nach dem Coulomb-Gesetz
einwirkende Kraft gleich
auf, indem Sie die auf das Elektron nach dem Coulomb-Gesetz
einwirkende Kraft gleich 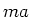 setzen. Hierbei ist
setzen. Hierbei ist 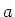 die Zentripetalbeschleunigung.
Zeigen Sie, daß bei jedem Abstand
die Zentripetalbeschleunigung.
Zeigen Sie, daß bei jedem Abstand 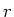 die kinetische
Energie halb so groß ist wie die potentielle Energie,
die kinetische
Energie halb so groß ist wie die potentielle Energie,
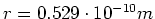 der Radius der
Elektronenbahn im Wasserstoffatom. Berechnen Sie
der Radius der
Elektronenbahn im Wasserstoffatom. Berechnen Sie
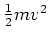 sowie
sowie 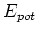 und die Gesamtenergie
und die Gesamtenergie
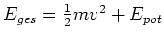 in Elektronenvolt. Die Energie
in Elektronenvolt. Die Energie 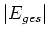 , die nötig ist, um das Elektron aus dem
Wasserstoffatom zu entfernen, heißt lonisierungsenergie.
, die nötig ist, um das Elektron aus dem
Wasserstoffatom zu entfernen, heißt lonisierungsenergie.
![\includegraphics[width=0.5\textwidth]{ue-03-06.eps}](img14.gif)
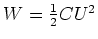 und vergleichen Sie das
Ergebnis mit dem Resultat aus Teil (4c).
und vergleichen Sie das
Ergebnis mit dem Resultat aus Teil (4c).
![\includegraphics[width=0.8\textwidth]{ue-03-04.eps}](img20.gif)
![\includegraphics[width=0.2\textwidth]{ue-03-02.eps}](img24.gif)
![\includegraphics[width=0.2\textwidth]{ue-03-03.eps}](img33.gif)
![\includegraphics[width=0.3\textwidth]{ue-03-05.eps}](img38.gif)
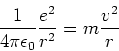
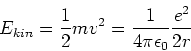
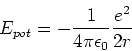
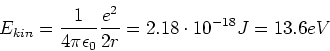
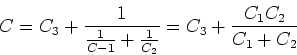
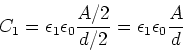
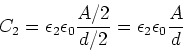
![\begin{displaymath}C = \frac{\epsilon_3}{2}C_0+ \frac{\epsilon_1 C_0 \epsilon_2 ...
...silon_2 }{\epsilon_1 + \epsilon_2 }\right]\epsilon_0\frac{A}{d}\end{displaymath}](img64.gif)
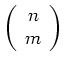 Ecken eines
Ecken eines 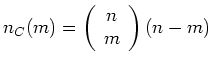 Kapazitäten.
Kapazitäten.
![\begin{displaymath}\frac{1}{C_{tot}} = \sum\limits_{m=0}^{n-1}\frac{1}{\left(\be...
...
m \\
\end{array}\right) \left(n-m\right)}\right]\frac{1}{C}\end{displaymath}](img86.gif)