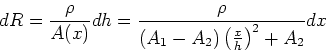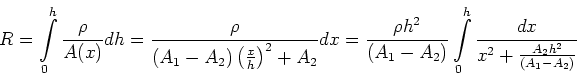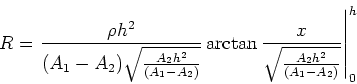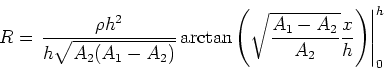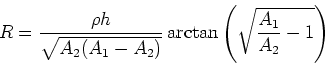Die Bestimmung des Widerstandes verlangt eine Berechnung des 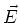 -Feldes
im Innern des Ohmschen Leiters. Wir definieren ein Koordinatensystem, bei dem
-Feldes
im Innern des Ohmschen Leiters. Wir definieren ein Koordinatensystem, bei dem 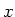 entlang der
Verbindungslinie der beiden Löcher liegt,
entlang der
Verbindungslinie der beiden Löcher liegt, 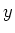 senkrecht dazu und parallel zur oberen Grenzfläche. Die
senkrecht dazu und parallel zur oberen Grenzfläche. Die
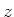 -Koordinate steht senkrecht zur Deckfläche. Die Scheibe habe die Dicke
-Koordinate steht senkrecht zur Deckfläche. Die Scheibe habe die Dicke 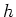 . Da der Strom keine Komponente
senkrecht zu den Scheibenflächen hat, gelten die
Randbedingungen an der unteren, bzw. oberen Scheibenfläche
. Da der Strom keine Komponente
senkrecht zu den Scheibenflächen hat, gelten die
Randbedingungen an der unteren, bzw. oberen Scheibenfläche
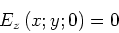 |
(1) |
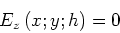 |
(2) |
Zudem muss das 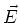 -Feld senkrecht auf den zylindrischen Mantelflächen zwischen Leiter und Elektroden
stehen (Äquipotentialflächen). Dies bedeutet insbesondere das Verschwinden
der
-Feld senkrecht auf den zylindrischen Mantelflächen zwischen Leiter und Elektroden
stehen (Äquipotentialflächen). Dies bedeutet insbesondere das Verschwinden
der 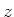 -Komponente des
-Komponente des 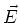 -Feldes. Somit drängt sich der Ansatz
-Feldes. Somit drängt sich der Ansatz
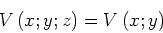 |
(3) |
auf. (3
) bedeutet das Verschwinden von 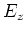 überall im Innern des Leiters. Wir haben also ein zweidimensionales
Potentialproblem vor uns (unabhängig von der Plattendicke
überall im Innern des Leiters. Wir haben also ein zweidimensionales
Potentialproblem vor uns (unabhängig von der Plattendicke 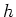 !). Die zylindrischen Mantelflächen zwischen
Leiter und Elektroden sind geladen, z.B. positiv oben, negativ unten. Da
!). Die zylindrischen Mantelflächen zwischen
Leiter und Elektroden sind geladen, z.B. positiv oben, negativ unten. Da 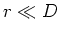 , können wir die
Beeinflussung der Ladungsverteilung oben durch die Ladungen unten vernachlässigen. An den Elektroden gilt
, können wir die
Beeinflussung der Ladungsverteilung oben durch die Ladungen unten vernachlässigen. An den Elektroden gilt
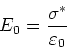 |
(4) |
Wir
haben somit eine homogene Ladungsverteilung auf der Mantelfläche, die wir durch die Ladungsdichte
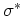 (Ladung pro Flächeneinheit) charakterisieren wollen. Unter diesen Umständen genügt es, das
(Ladung pro Flächeneinheit) charakterisieren wollen. Unter diesen Umständen genügt es, das
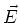 -Feld auf der Symmetrieachse zu kennen. Es setzt sich zusammen aus den Feldern
-Feld auf der Symmetrieachse zu kennen. Es setzt sich zusammen aus den Feldern 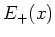 der
positiven Ladungen oben und
der
positiven Ladungen oben und 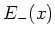 (negativen Ladungen unten). Das Gausssche Gesetz
bezüglich des Kreiszylinders mit Radius
(negativen Ladungen unten). Das Gausssche Gesetz
bezüglich des Kreiszylinders mit Radius 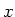 (Höhe
(Höhe 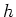 ) liefert die Beziehung
) liefert die Beziehung
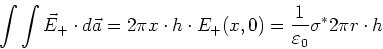 |
(5) |
Aus (5
) folgt
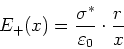 |
(6) |
Analog findet man
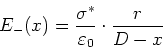 |
(7) |
Das Linienintegral berechnet sich mit (6
) und (7
) zu
(Im letzten Schritt wurde 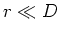 verwendet.)
verwendet.)
Der totale Strom wird durch Integration über die Elektrodenflächen bestimmt.
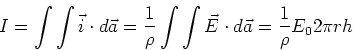 |
(9) |
Mit Gleichung (4) erhalten wir
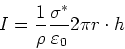 |
(10) |
Mit 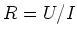 bekommen wir für den Widerstand
bekommen wir für den Widerstand
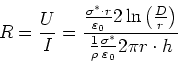 |
(11) |
Wir erhalten
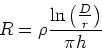 |
(12) |
Es ist interessant zu bemerken, dass das Feldlinienbild des Stromdichtefeldes 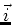 dieses Problems
identisch ist mit demjenigen des
dieses Problems
identisch ist mit demjenigen des 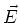 -Feldes zweier unendlich langer, homogen geladener Drähte.
-Feldes zweier unendlich langer, homogen geladener Drähte.
Wir haben uns hier mit der stationären Stromverteilung im homogenen Ohmschen Leiter beschäftigt. Die
Resultate bleiben auch für ''Quasistationäre'' Verhältnisse gültig, z.B. für zeitabhängige Wechselspannungen,
solange die Frequenzen nicht zu gross sind (d.h. unter Vernachlässigung der Induktionseffekte).
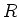 fliessende Strom
fliessende Strom 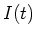 ; skizziere den Verlauf.
; skizziere den Verlauf.
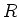 herrschende Spannung
herrschende Spannung 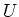 im Gleichgewichtszustand?
im Gleichgewichtszustand?
![\includegraphics[width=0.4\textwidth]{ue-04-02.eps}](img17.gif)
![\includegraphics[width=0.4\textwidth]{ue-04-03.eps}](img22.gif)
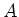 und
und 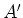 ?
?
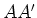 die
Spannung
die
Spannung 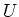 legt, welche Spannung misst man dann zwischen den Lötstellen der
ersten Sprosse, der zweiten
Sprosse usw.?
legt, welche Spannung misst man dann zwischen den Lötstellen der
ersten Sprosse, der zweiten
Sprosse usw.?
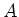 und
und 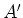 und die Spannungen an den verbleibenden Sprossen nicht
ändern? Hinweis: Wie ändert sich der Widerstand zwischen
und die Spannungen an den verbleibenden Sprossen nicht
ändern? Hinweis: Wie ändert sich der Widerstand zwischen 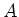 und
und 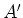 , wenn
Sie die ohnehin schon sehr lange Leiter um eine weitere Sprosse (
, wenn
Sie die ohnehin schon sehr lange Leiter um eine weitere Sprosse (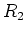 ) und
die beiden Holmstücke (
) und
die beiden Holmstücke (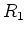 ) nach oben verlängern?
) nach oben verlängern?
![\includegraphics[width=0.7\textwidth]{ue-04-01.eps}](img34.gif)
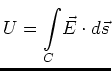
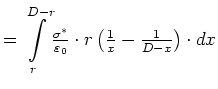
![$\textstyle =\frac{\sigma^{\ast}\cdot r}{\varepsilon_{0}}\left[ \left. \ln
x\right\vert _{r}^{D-r}-\left. \ln\left( D-x\right) \right\vert _{r}%%
^{D-r}\right]$](img71.gif)
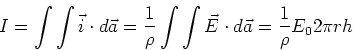
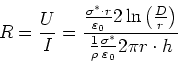
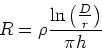
![\includegraphics[width=0.5\textwidth]{ue-04-06.eps}](img80.gif)
![\includegraphics[width=0.65\textwidth]{ue-04-04.eps}](img94.gif)
![\includegraphics[width=0.45\textwidth]{ue-04-05.eps}](img95.gif)
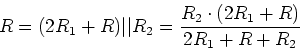
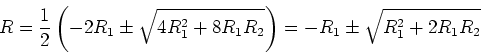
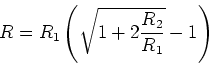
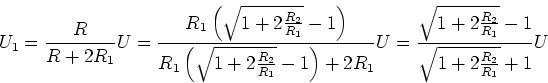
![\begin{displaymath}U_n = \left[\frac{\sqrt{1+2\frac{R_2}{R_1}}-1}
{\sqrt{1+2\frac{R_2}{R_1}}+1}\right]^nU\end{displaymath}](img104.gif)
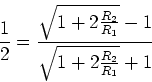
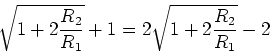
![\includegraphics[width=0.5\textwidth]{ue-04-CR-laden.eps}](img138.gif)
![\includegraphics[width=0.5\textwidth]{ue-04-CR-entladen.eps}](img149.gif)