Materialien
Übungsblatt 03 vom 14. 11. 2002 (HTML oder PDF)
Folien zur Vorlesung am 14. 11. 2002 (PDF)
Wir betrachten ein Modellatom bestehend aus einem Kern der Ladung ![]() und einer Elektronenwolke der Ladung
und einer Elektronenwolke der Ladung
![]() . Ohne äusseres Feld liegen die Ladungsschwerpunkte übereinander.
. Ohne äusseres Feld liegen die Ladungsschwerpunkte übereinander.
![\includegraphics[width=0.6\textwidth]{elektrostatik-016.eps}](img356.gif)
Schematisches Bild eines Atoms mit seiner Elektronenhülle
|
Das Kräftegleichgewicht lautet:
Das induzierte Dipolmoment ist
| (2.95) |
und damit
Dabei ist ![]() die atomare Polarisierbarkeit (Einheit
die atomare Polarisierbarkeit (Einheit
![]() ).
).
gefüllte Elektronenschale
| Atom oder Molekül |
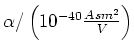 |
| He | 0.2 |
| Li |
0.03 |
| Ne | 0.4 |
| K |
0.9 |
| Xe | 3.5 |
| O |
3.5 |
| CCL |
10 |
| CL |
4 |
| I |
7 |
nicht gefüllte Elektronenschale
| Atom oder Molekül |
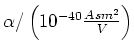 |
| H | 0.7 |
| Li | 13 |
| K | 38 |
| Cs | 46 |
Die potentielle Energie des induzierten Dipols im homogenen Feld
![]() ist
ist
| (2.97) |
da
| (2.98) |
und damit
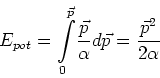 |
(2.99) |
Versuch zur Vorlesung: Plattenkondensator mit
Dielektrikum ES-3
Bis jetzt haben wir angenommen, dass das elektrische Feld im Vakuum gemessen
wurde. Dann gilt
| (2.100) |
![\includegraphics[width=0.5\textwidth]{elektrostatik-017.eps}](img371.gif)
Isolatoren in einem Kondensatoren
|
Die Beziehung zwischen angelegter Spannung und dem elektrischen Feld ist
| (2.101) |
unabhängig von den Eigenschaften des Isolationsmaterials.
Andererseits ist
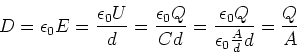 |
(2.102) |
abhängig von der gespeicherten Ladung. Am Kondensator können D und E unabhängig bestimmt werden.
In vielen Fällen sind ![]() und
und ![]() linear voneinander abhängig.
linear voneinander abhängig.
mit
![]() und
und
![]()
![]() heisst die Dielektrizitätskonstante,
heisst die Dielektrizitätskonstante, ![]() die dielektrische Suszeptibilität.
die dielektrische Suszeptibilität.
Im allgemeinen sind ![]() und
und ![]() Tensoren.
Tensoren.
| Material | |
| Vakuum | 1 |
| Luft | 1.0006 |
| Paraffin | 2.1 |
| Glas | 5-9 |
| Wasser(291k, 0Hz) | 81 |
| Wasser (291k, 1PHz | 1,77 |
Alle Formeln der Elektrostatik können auf Dielektrika angewandt werden, indem ![]() durch
durch
![]() ersetzt wird.
ersetzt wird.
Woher rührt ![]() ?
?
Wenn ein Material ortsfeste permanente elektrische Dipole besitzt, dann werden diese im extremen Feld ausgerichtet. Die Ladungen im Inneren des Materials kompensieren sich. An der Oberfläche treten Ladungen auf, die das äussere Feld schwächen.
![\includegraphics[width=0.6\textwidth]{elektrostatik-018.eps}](img383.gif)
|
Dabei werden die positiven Ladungen an der Oberfläche angereichert, in die das elektrische Feld zeigt. Die negativen Ladungen werden auf der Gegenseite angereichert. Diese Polarisation heisst Orientierungspolarisation.
![\includegraphics[width=0.6\textwidth]{elektrostatik-019.eps}](img384.gif)
Links: unpolares Medium ohne äusseres elektrisches Feld. Rechts: mit einem nach links gerichteten elektrischen Feld.
|
Ein unpolares Medium wird durch das äussere Feld nach Gleichung (2.104) polarisiert. Die Ladungsschwerpunkte der Elektronen verschieben sich und wieder entsteht ein inneres elektrisches Feld, das dem äusseres Feld entgegen wirkt. Diese Polarisation ist die Verschiebungspolarisation.
Im ladungsfreien Raum gilt
![]() (siehe Gleichung (2.19) ). Da das elektrostatische Feld ein
konservatives Feld ist, gilt auch
(siehe Gleichung (2.19) ). Da das elektrostatische Feld ein
konservatives Feld ist, gilt auch
![]() . Wir betrachten eine Oberfläche
. Wir betrachten eine Oberfläche ![]() , die ein Stück
, die ein Stück
![]() der Grenzfläche umschliesst. Dann ist
der Grenzfläche umschliesst. Dann ist
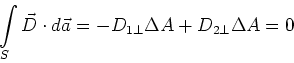
und damit gilt für die dielektrische Verschiebung die folgende Stetigkeitsbedingung
| (2.104) |
Wir verwenden weiter eine Schlaufe ![]() , die die Grenzfläche zweimal durchdringt und erhalten
, die die Grenzfläche zweimal durchdringt und erhalten
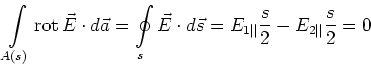
| (2.105) |
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{An...
...Feldes parallel zur Grenzfl{\uml a}che
\end{itemize}sind stetig.}\end{minipage}}](img393.gif)
Mit
![]() können diese Stetigkeitsbedingungen auch für das
Potential
können diese Stetigkeitsbedingungen auch für das
Potential ![]() umgeschrieben werden
umgeschrieben werden
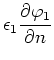 |
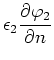 |
(2.106) |
In diesem Abschnitt wollen wir aus einer mikroskopische Betrachtung einen Zusammenhang zwischen der relativen Dielektrizitätszahl und der Polarisierbarkeit ableiten. Die Polarisation ist wie folgt definiert:
wobei ![]() die Dichte der induzierten Dipole ist.
die Dichte der induzierten Dipole ist.
![\includegraphics[width=0.7\textwidth]{elektrostatik-033.eps}](img401.gif)
|
Wir betrachten ein homogenes Dielektrikum mit ![]() , bei dem ein kugelförmiges kleines Volumen mit dem
Radius
, bei dem ein kugelförmiges kleines Volumen mit dem
Radius ![]() entfernt wurde.
In diesem Volumen berechnen wir das lokale Feld[Som78, 68],das von einem externen Feld
entfernt wurde.
In diesem Volumen berechnen wir das lokale Feld[Som78, 68],das von einem externen Feld ![]() in der
in der ![]() -Richtung hervorgerufen wird. Das Dielektrikum erzeugt an der
Oberfläche des Hohlraums eine Ladungsdichte
-Richtung hervorgerufen wird. Das Dielektrikum erzeugt an der
Oberfläche des Hohlraums eine Ladungsdichte
![]() . Nach dem Coulombgesetz
(Gleichung (2.5) ) ist der Beitrag von
. Nach dem Coulombgesetz
(Gleichung (2.5) ) ist der Beitrag von ![]() gegeben durch
gegeben durch
| (2.108) |
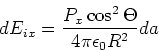 |
(2.109) |
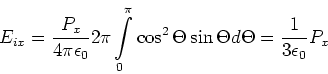 |
(2.110) |
| (2.112) |
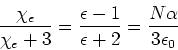 |
(2.113) |
![\includegraphics[width=0.6\textwidth]{elektrostatik-020.eps}](img414.gif)
Links: Kondensator ohne und rechts: mit Dielektrikum
|
Wir betrachten einen Kondensator, dessen Platten die konstante Ladung Q tragen. Das Feld im Inneren des
Kondensators sei um den Faktor ![]() geringer als das Feld
geringer als das Feld ![]() ohne Dielektrikum
ohne Dielektrikum
| (2.114) |
Bei einem Plattenkondensator mit dem Abstand ![]() ist
ist
| (2.115) |
Die Kapazität ist
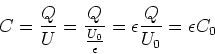 |
(2.116) |
Also ist beim Plattenkondensator
| (2.117) |
Die dielektrische Verschiebung ist im obigen Falle konstant
| (2.118) |
Hält man die Spannung fest, wenn ein Dielektrikum in den Kondensator eingebracht wird ist,
| (2.119) |
Materialien
Folien zur Vorlesung am 21. 11. 2002 (PDF)
Versuch zur Vorlesung: Steighöhe im
Kondensator ES-12
Die Energiedichte im Kondensator ist
![\includegraphics[width=0.6\textwidth]{elektrostatik-021.eps}](img424.gif)
Links eine dielektrische Flüssigkeit im Kondensator ohne angelegtes Feld. Rechts mit angelegtem Feld.
|
Wenn wir das obige Experiment durchführen, steigt die dielektrische Flüssigkeit. Dabei erhöht sich die im elektrischen Feld gespeicherte Energie und auch die potentielle Energie.
Wie geht das?
![\includegraphics[width=0.8\textwidth]{elektrostatik-022.eps}](img425.gif)
Skizze der Änderungen beim Anlegen einer Spannung
|
Zur Berechnung müssen wir auch die Batterie oder Spannungsquelle mit betrachten[Kän78].
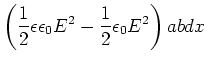 |
|||
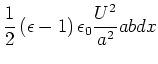 |
|||
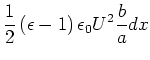 |
(2.121) |
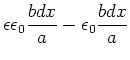 |
|||
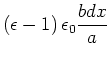 |
(2.122) |
| (2.123) | |||
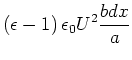 |
| (2.124) |
| (2.125) |
| (2.126) |