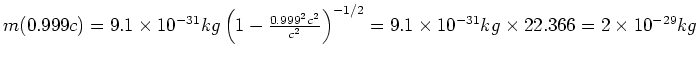

Up: Grundkurs IIIb für Physiker
Übungsblatt 05
Grundkurs IIIb für Physiker
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
16. 12. 2002 oder 13. 1. 2003
Elektrische Eigenschaften der Materie, Ströme,
- In einem geschlossenen kreisförmigen Leiter (Kreisradius
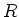 ) fliesse der Strom
) fliesse der Strom 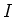 .
.
- Berechnen Sie die allgemeine Gleichung für
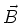 im Punkt
im Punkt 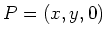 , wobei die
, wobei die 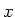 -Achse
die Senkrechte auf die Kreisebene durch den Kreismittelpunkt ist (der Durchstosspunkt sei
-Achse
die Senkrechte auf die Kreisebene durch den Kreismittelpunkt ist (der Durchstosspunkt sei 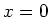 .
.
- Berechnen Sie
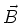 auf der
auf der 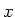 -Achse.
-Achse.
- Berechnen Sie
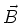 auf der Ebene
auf der Ebene 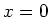 für
für 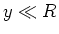 . Verwende eine Serienentwicklung bis
zum ersten nicht verschwindenden Glied.
. Verwende eine Serienentwicklung bis
zum ersten nicht verschwindenden Glied.
- Berechnen Sie
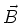 für einen allgemeinen Punkt unter Verwendung einer vernünftigen
Serienentwicklung.
für einen allgemeinen Punkt unter Verwendung einer vernünftigen
Serienentwicklung.
- Zwei der Kreisströme aus der Aufgabe 1 sollen parallel zueinander im Abstand
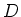 so angeordnet sein,
dass ihre Rotationssymmetrieachsen zusammenfallen. Definiere dazu ein Koordinatensystem, bei dem
die
so angeordnet sein,
dass ihre Rotationssymmetrieachsen zusammenfallen. Definiere dazu ein Koordinatensystem, bei dem
die 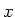 -Achse die Symmetrieachse ist, mit dem Nullpunkt in der Mitte zwischen den beiden
Kreisströmen.
-Achse die Symmetrieachse ist, mit dem Nullpunkt in der Mitte zwischen den beiden
Kreisströmen.
- Stellen Sie eine Gleichung für
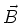 auf.
auf.
- Lösen Sie die Gleichung für den Symmetriepunkt.
- Geben Sie eine Näherungslösung für die Umgebung des Symmetriepunktes an.
- Eine Elektrolok Re6/6 hat sechs Fahrmotoren die je auf eine Achse wirken.
Sie hat eine Leistung von
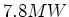 . Die Motoren werden
mit einer Spannung von
. Die Motoren werden
mit einer Spannung von 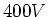 angesteuert. Sie sollen als Leiterschlaufen mit einer Länge von
angesteuert. Sie sollen als Leiterschlaufen mit einer Länge von 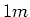 (parallel
zur Drehachse) und einem Abstand von
(parallel
zur Drehachse) und einem Abstand von 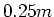 von der Drehachse modelliert werden. Die Motoren laufen
mit der
von der Drehachse modelliert werden. Die Motoren laufen
mit der 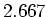 -fachen Drehzahl wie die Antriebsräder, die einen Durchmesser von
-fachen Drehzahl wie die Antriebsräder, die einen Durchmesser von 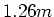 haben. Die
Zugkraft ist
haben. Die
Zugkraft ist 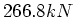
- Welches Drehmoment wirkt an jeder Achse?
- Welches Drehmoment wirkt an jedem Motor?
- Berechnen Sie aus den Anschlusswerten den Motorstrom.
- Wie gross muss die magnetische Induktion
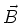 sein?
sein?
- Wie viele Leiterwindungen wird der Anker haben (machen Sie realistische Annahmen)?
- In einer Leitung, die parallel zur
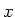 -Achse liegt, befindet sich flüssiges Natrium.
Entlang der
-Achse liegt, befindet sich flüssiges Natrium.
Entlang der 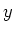 -Achse wird die magnetische Induktion
-Achse wird die magnetische Induktion 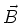 angelegt. Entlang der
angelegt. Entlang der 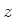 -Achse fliesst der
Strom
-Achse fliesst der
Strom 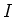 . Was soll die Anordnung bewirken?
. Was soll die Anordnung bewirken?
- In einem Synchrotron (kreisförmige Anordnung mit
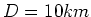 bewegen sich Elektronen mit
bewegen sich Elektronen mit
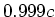 .
.
- Berechnen sie die homogene magnetische Induktion
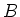 , die die Elektronen auf der Kreisbahn hält.
, die die Elektronen auf der Kreisbahn hält.
- Wie muss
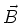 angeordnet sein?
angeordnet sein?
- Eine Metallscheibe mit dem Radius
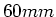 sei auf einer reibungsfreien Achse montiert. Durch die
Achse und die Scheibe kann ein Strom fliessen, der am Rand der Scheibe über einen Schleifkontakt
zugeführt wird. Parallel zur Scheibenachse verlaufe ein homogenes Magnetfeld mit
sei auf einer reibungsfreien Achse montiert. Durch die
Achse und die Scheibe kann ein Strom fliessen, der am Rand der Scheibe über einen Schleifkontakt
zugeführt wird. Parallel zur Scheibenachse verlaufe ein homogenes Magnetfeld mit 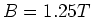 . Bei
einer Stromstärke von
. Bei
einer Stromstärke von 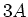 rotiert die Scheibe mit einer konstanten Kreisfrequenz. Wie gross ist die
Reibungskraft am Schleifkontakt?
rotiert die Scheibe mit einer konstanten Kreisfrequenz. Wie gross ist die
Reibungskraft am Schleifkontakt?
- Zeigen Sie, dass der Radius der Bahn eines geladenen Teilchens in einem Zyklotron
proportional zur Quadratwurzel der schon vollendeten Umläufe ist.
- Beryllium hat eine Dichte von
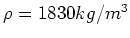 und eine molare Masse von
und eine molare Masse von
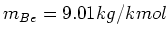 . Ein
Berylliumstab der Dicke
. Ein
Berylliumstab der Dicke 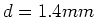 und der Breite
und der Breite 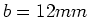 werde von einem Strom von
werde von einem Strom von 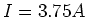 durchflossen.
Der Stab befindet sich in einem Magnetfeld von
durchflossen.
Der Stab befindet sich in einem Magnetfeld von 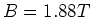 senkrecht zum Stab (parallel zur Dicke). Es wird
eine Hall-Spannung von
senkrecht zum Stab (parallel zur Dicke). Es wird
eine Hall-Spannung von
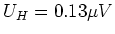 gemessen.
gemessen.
- Wie gross ist die Ladungsträgerdichte in Beryllium?
- Wie gross ist die Anzahl Atome pro
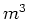 ?
?
- Wie gross ist die Anzahl der freien Elektronen pro Gitteratom?
- Wir rechnen für einen Punkt in der
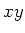 -Ebene. Das problem ist rotationssymmetrisch
um die
-Ebene. Das problem ist rotationssymmetrisch
um die 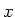 -Achse.
-Achse.
- Beobachtungspunkt
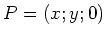
- Punkt auf Leiterschleife
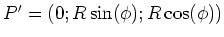
-
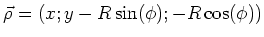
-
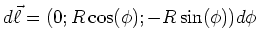
-
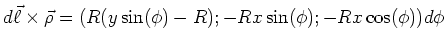
-
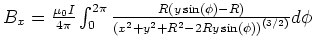
-
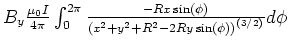
-
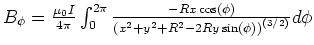
- Die Bestimmungsgleichung wird
-
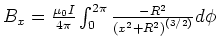
-
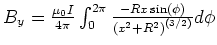
-
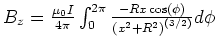
- Die Integrale für
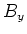 und
und 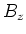 haben eine Winkelfunktion mit der Potenz 1:
deshalb sind sie null.
haben eine Winkelfunktion mit der Potenz 1:
deshalb sind sie null.
-
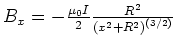
- Das resultierende Magnetfeld hat also nur eine
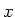 -Komponente und keine radiale
Komponente.
-Komponente und keine radiale
Komponente.
- Die Serienentwicklung für
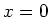 und
und 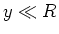
-
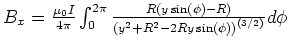
-
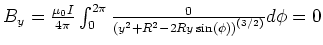
-
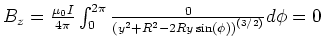
-
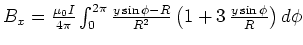
-
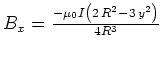
- Das resultierende Magnetfeld hat also nur eine
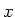 -Komponente und keine radiale
Komponente.
-Komponente und keine radiale
Komponente.
- Wir haben
-
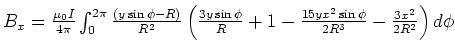
-
![$B_y = -\frac{\mu_0
I}{4\pi}\int_0^{2\pi}\frac{x\sin \phi}{R^2}
\left[ {\frac ...
...ac {15y{x}^{2}\sin\phi }{2R^3 }}-
{\frac {3{x}^{2}}{ 2{R}^{2}}} \right]
d\phi$](img53.gif)
-
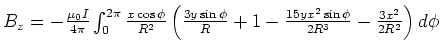
- Diese Integrale ergeben
-
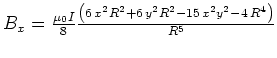
-
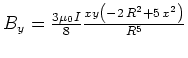
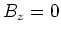
- Wir sehen also, dass in diesem Falle das Magnetfeld eine Komponente in die
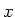 -Richtung und eine in radiale Richtung hat.
-Richtung und eine in radiale Richtung hat.
- Beobachtungspunkt
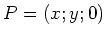
- Punkte auf Leiterschleife
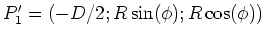 und
und
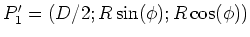
-
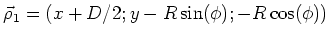 und
und
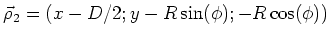
-
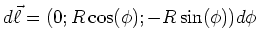
-
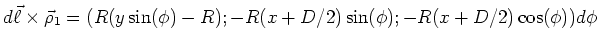 und
und
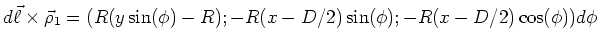
-
![$B_x = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{R(y\sin(\phi)-R)}{\left((...
...n(\phi)-R)}{\left((x-D/2)^2+y^2+R^2-2Ry\sin(\phi)\right)^{(3/2)}}
\right]d\phi$](img64.gif)
-
![$B_y = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R(x+D/2)\sin(\phi)}{\lef...
...\sin(\phi)}{\left((x-D/2)^2+y^2+R^2-2Ry\sin(\phi)\right)^{(3/2)}}
\right]d\phi$](img65.gif)
-
![$B_z = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R(x+D/2)\cos(\phi)}{\lef...
...\cos(\phi)}{\left((x-D/2)^2+y^2+R^2-2Ry\sin(\phi)\right)^{(3/2)}}
\right]d\phi$](img66.gif)
- Am Symmetriepunkt ist
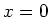 und
und 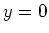
-
![$B_x = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R^2}{\left(D^2/4+R^2\right)^{(3/2)}}+
\frac{-R^2}{\left(D^2/4+R^2\right)^{(3/2)}}
\right]d\phi$](img68.gif)
-
![$B_y = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R(D/2)\sin(\phi)}{\left(...
...(3/2)}}+
\frac{R(D/2)\sin(\phi)}{\left(D^2/4+R^2\right)^{(3/2)}}
\right]d\phi$](img69.gif)
-
![$B_z = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R(D/2)\cos(\phi)}{\left(...
...(3/2)}}+
\frac{R(D/2)\cos(\phi)}{\left(D^2/4+R^2\right)^{(3/2)}}
\right]d\phi$](img70.gif)
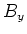 und
und 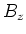 haben je eine ungradzahlige Potenz einer Winkelfunktion. Also ist
haben je eine ungradzahlige Potenz einer Winkelfunktion. Also ist
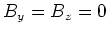
-
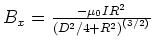
- Die Reihenentwicklung bis zur ersten nicht verschwindenden Ordnung ergibt
-
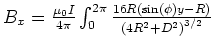
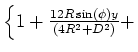
![$\left. \frac{{x}^{2}}{\left( 4{R}^{2}+{D
}^{2}\right) }\left[ \left( {-6}+{\fr...
...rac{7{D}^{2}}{\left( 4{R}^{2}+{D}\right)
^{2}}}\right) \right] \right\}
d\phi$](img75.gif)
-
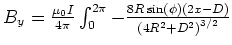
![$\left. \frac{{x}^{2}}{\left( 4{R}^{2}+{D
}^{2}\right) }\left[ \left( {-6}+{\fr...
...rac{7{D}^{2}}{\left( 4{R}^{2}+{D}\right)
^{2}}}\right) \right] \right\}
d\phi$](img75.gif)
-
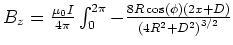
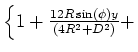
![$\left. \frac{{x}^{2}}{\left( 4{R}^{2}+{D
}^{2}\right) }\left[ \left( {-6}+{\fr...
...rac{7{D}^{2}}{\left( 4{R}^{2}+{D}\right)
^{2}}}\right) \right] \right\}
d\phi$](img75.gif)
- Die Lösungen sind
-
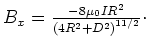
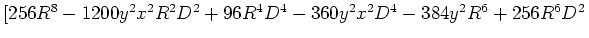
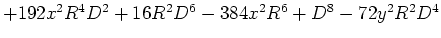
![$\left. +168{x}^{2}{R}^{2}{D}^{4}+24{x}^{2}{D} ^{6}+960{y}^{2}{x}^{2}{R}^{4}-6{y}^{2}{D}^{6}-288{y}^{2}{R}
^{4}{D}^{2}\right] $](img81.gif)
-
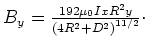
![$\left[
7{R}^{2}{D}^{4}+8{R}^{4}{D }^{2}+{D}^{6}-15{x}^{2}{D}^{4}-50{x}^{2}{R}
^{2}{D}^{2}-16{R}^{6}+40{x}^{2}{R}^{4}\right] $](img83.gif)
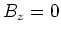
- Die Anfahrzugkraft ist
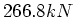 und verteilt sich auf 6 Achsen.
und verteilt sich auf 6 Achsen.
- Pro Achse ist die Zugkraft
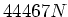
- Die Räder haben
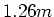 Durchmesser.
Durchmesser.
- das Drehmoment pro Achse ist
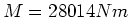
- Da der Motor sich
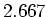 mal schneller als die Achse dreht, ist das Drehmoment
am Motor
mal schneller als die Achse dreht, ist das Drehmoment
am Motor
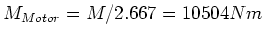
- Die Gesamtleistung ist
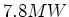
- Die Leistung pro Motor ist
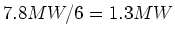
- Aus
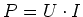 folgt
folgt
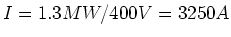
- Aus der Vorlesung: das magnetische Moment einer Leiterschleife ist maximal
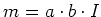
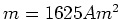
- Das Drehmoment ist
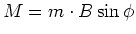
- Also ist
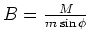
- Wir setzen
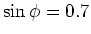 (ein guter Mittelwert)
(ein guter Mittelwert)
- also:
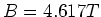 bei einer Leiterschlaufe
bei einer Leiterschlaufe
- Nehmen wir an, wir hätten 50 Windungen, dann wäre
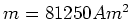 und
und 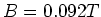 ,
realistische Grössen.
,
realistische Grössen.
- Die Elektronen werden durch die Lorentz-Kraft in Richtung der Röhre abgelenkt. Da sie mit den
Natriumatomen stossen, übertragen sie einen Impuls in Richtung der Röhre und pumpen so das flüssige
Metall.
- Die Masse der Elektronen ist:
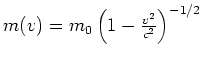 oder
oder
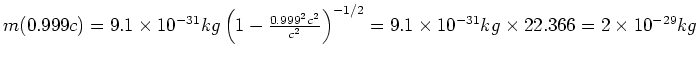
- Zentripetalkraft
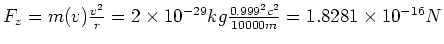
- Die Zentripetalkraft muss gleich der Lorentzkraft sein, also
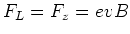
-
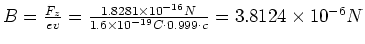
- Da die Magnete nicht auf der ganzen Länge des Synchrotrons verteilt sind, sondern ein Polygon
bilden, sind grössere Magnetfelder nötig.
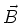 muss senkrecht zur Ringebene stehen.
muss senkrecht zur Ringebene stehen.
- Fliesst der Strom durch eine Scheibe in einem Magnetfeld, so wirkt die Kraft
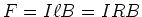 Die Kraft ist gleichmässig über die Scheibe vom Rand bis zur Achse verteilt. Daher ist das von ihr
verursachte Drehmoment
Die Kraft ist gleichmässig über die Scheibe vom Rand bis zur Achse verteilt. Daher ist das von ihr
verursachte Drehmoment
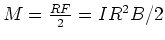 . Die Reibungskraft wirkt nur am Radius
. Die Reibungskraft wirkt nur am Radius 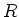 . Also
ist
. Also
ist 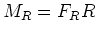 und damit
und damit
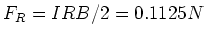
- Wenn
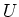 die Spannung an den Elektroden ist, dann gewinnt ein Teilchen der Ladung
die Spannung an den Elektroden ist, dann gewinnt ein Teilchen der Ladung 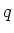 bei jedem
Umlauf die Energie
bei jedem
Umlauf die Energie 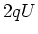 . Nach
. Nach 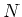 Umläufen hat das Teilchen die kinetische Energie
Umläufen hat das Teilchen die kinetische Energie
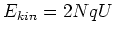 .
Mit
.
Mit 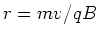 (Aus Zentripetalkraft und Lorentzkraft) und
(Aus Zentripetalkraft und Lorentzkraft) und
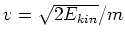 folgt
folgt
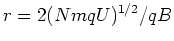 folgt die Behauptung.
folgt die Behauptung.
-
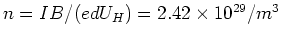
- Die Zahlendichte der Atome ist die Dichte, geteilt durch die molare Masse
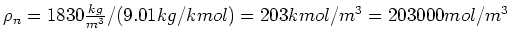 . Multipliziert mit der Avogadrozahl
. Multipliziert mit der Avogadrozahl
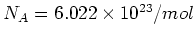 ergibt
ergibt
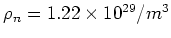
- Die Division der beiden Resultate ergibt
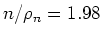 Elektronen pro Atom.
Elektronen pro Atom.
Übungsblatt 05
Grundkurs IIIb für Physiker
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt05
The translation was initiated by marti on 2003-01-13


Up: Grundkurs IIIb für Physiker
Othmar Marti
Experimentelle Physik
Universiät Ulm
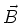 im Punkt
im Punkt 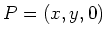 , wobei die
, wobei die 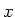 -Achse
die Senkrechte auf die Kreisebene durch den Kreismittelpunkt ist (der Durchstosspunkt sei
-Achse
die Senkrechte auf die Kreisebene durch den Kreismittelpunkt ist (der Durchstosspunkt sei 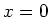 .
.
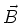 auf der
auf der 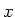 -Achse.
-Achse.
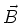 auf der Ebene
auf der Ebene 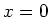 für
für 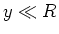 . Verwende eine Serienentwicklung bis
zum ersten nicht verschwindenden Glied.
. Verwende eine Serienentwicklung bis
zum ersten nicht verschwindenden Glied.
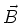 für einen allgemeinen Punkt unter Verwendung einer vernünftigen
Serienentwicklung.
für einen allgemeinen Punkt unter Verwendung einer vernünftigen
Serienentwicklung.
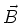 auf.
auf.
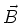 sein?
sein?
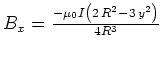
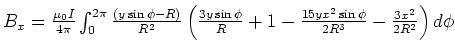
![$B_y = -\frac{\mu_0
I}{4\pi}\int_0^{2\pi}\frac{x\sin \phi}{R^2}
\left[ {\frac ...
...ac {15y{x}^{2}\sin\phi }{2R^3 }}-
{\frac {3{x}^{2}}{ 2{R}^{2}}} \right]
d\phi$](img53.gif)
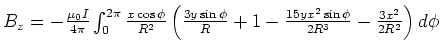
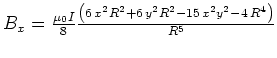
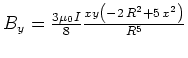
![$B_x = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{R(y\sin(\phi)-R)}{\left((...
...n(\phi)-R)}{\left((x-D/2)^2+y^2+R^2-2Ry\sin(\phi)\right)^{(3/2)}}
\right]d\phi$](img64.gif)
![$B_y = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R(x+D/2)\sin(\phi)}{\lef...
...\sin(\phi)}{\left((x-D/2)^2+y^2+R^2-2Ry\sin(\phi)\right)^{(3/2)}}
\right]d\phi$](img65.gif)
![$B_z = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R(x+D/2)\cos(\phi)}{\lef...
...\cos(\phi)}{\left((x-D/2)^2+y^2+R^2-2Ry\sin(\phi)\right)^{(3/2)}}
\right]d\phi$](img66.gif)
![$B_x = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R^2}{\left(D^2/4+R^2\right)^{(3/2)}}+
\frac{-R^2}{\left(D^2/4+R^2\right)^{(3/2)}}
\right]d\phi$](img68.gif)
![$B_y = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R(D/2)\sin(\phi)}{\left(...
...(3/2)}}+
\frac{R(D/2)\sin(\phi)}{\left(D^2/4+R^2\right)^{(3/2)}}
\right]d\phi$](img69.gif)
![$B_z = \frac{\mu_0
I}{4\pi}\int_0^{2\pi}\left[
\frac{-R(D/2)\cos(\phi)}{\left(...
...(3/2)}}+
\frac{R(D/2)\cos(\phi)}{\left(D^2/4+R^2\right)^{(3/2)}}
\right]d\phi$](img70.gif)
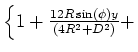
![$\left. \frac{{x}^{2}}{\left( 4{R}^{2}+{D
}^{2}\right) }\left[ \left( {-6}+{\fr...
...rac{7{D}^{2}}{\left( 4{R}^{2}+{D}\right)
^{2}}}\right) \right] \right\}
d\phi$](img75.gif)
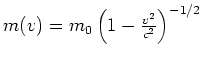 oder
oder