|
|
Materialien
Folien zur Vorlesung vom 11. 11. 2004: PDF Seminar vom 11. 11. 2004: Aufgabenblatt 02 (HTML oder PDF) |

| Dieser Stoff wurde am 11. 11. 2004 behandelt |
|
|
Materialien
Folien zur Vorlesung vom 11. 11. 2004: PDF Seminar vom 11. 11. 2004: Aufgabenblatt 02 (HTML oder PDF) |
Die Arbeit ist durch
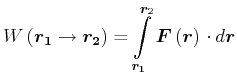 |
(2.37) |
definiert.
Die potentielle Energie eines Kraftfeldes
![]() ist die Arbeit gegen diese Feldkraft.
Nach dem 3. Newtonschen Axiom ist
ist die Arbeit gegen diese Feldkraft.
Nach dem 3. Newtonschen Axiom ist
![]() . Also
. Also
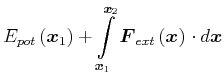 |
(2.38) | ||
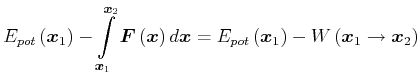 |
(2.39) |
Eine potentielle Energie existiert, wenn
Die potentielle Energie einer Probeladung ![]() im Feld der Ladung
im Feld der Ladung ![]() ist
ist
![\includegraphics[width=0.99\textwidth]{elektrostatik-030}](img362.gif)
|
Da wir jede Bahnkurve durch Stücke in radialer Richtung und durch Bahnen mit
![]() approximieren
können, und da die Bahnen auf den Kugelflächen keinen Beitrag geben (sie sind senkrecht zur Kraft) können wir das
Integral vereinfachen.
approximieren
können, und da die Bahnen auf den Kugelflächen keinen Beitrag geben (sie sind senkrecht zur Kraft) können wir das
Integral vereinfachen.
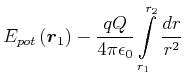 |
(2.41) | ||
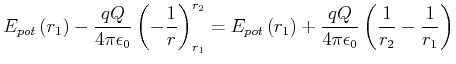 |
Üblicherweise setzt man
![]() . Damit wird
. Damit wird
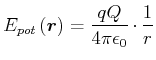 |
(2.42) |
Aus der potentiellen Energie kann die Kraft mit dem Gradienten
| (2.43) |
berechnet werden. Für die potentielle Energie der Coulomb-Kraft bekommen wir
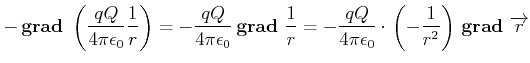 |
|||
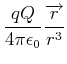 |
(2.44) |
In Komponenten ist
![]() und
und
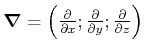
Also
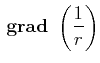 |
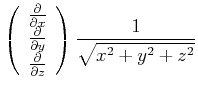 |
||
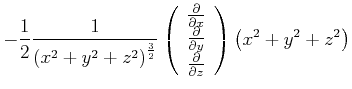 |
|||
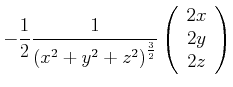 |
|||
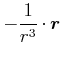 |
(2.45) |
Ergänzend zu Coulomb-Kraft hatten wir das elektrische Feld als auf eine Einheitsladung normierte Grösse eingeführt.
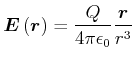 |
(2.46) |
Die potentielle Energie der Ladung ![]() im Feld der Ladung
im Feld der Ladung ![]() , normiert auf
, normiert auf ![]() ist das
elektrische Potential
ist das
elektrische Potential ![]() , auch Spannung
, auch Spannung
![]() genannt. Ich verwende in diesem Skript die Begriffe elektrisches Potential und Spannung
austauschbar.
genannt. Ich verwende in diesem Skript die Begriffe elektrisches Potential und Spannung
austauschbar.
Wichtig ist die Beziehung
| (2.48) |
Wie die Kraft aus der potentiellen Energie über die Gradientenbildung hervorgeht, wird das elektrische Feld mit
| (2.49) |
berechnet.
Folgende Relationen gelten
Wir merken uns
analog zur potentiellen Energie.
Die Einheit des elektrostatischen Potentials oder der Spannung ist
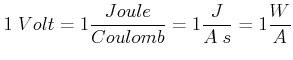
Das Gravitationspotential ist
![]() .
.
Da die Coulomb-Kräfte additiv sind, ist auch das elektrostatische Potential oder die elektrostatische potentielle
Energie additiv. Das Potential von Ladungen ![]() an den Orten
an den Orten ![]() ist also
ist also
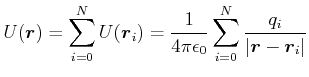 |
(2.52) |
Für kontinuierliche Ladungsverteilungen
![]() ist das Potential
ist das Potential
|
|
Das elektrostatische Potential eines Kreisringes mit der Ladung ![]() und dem Radius
und dem Radius ![]() im Abstand
im Abstand ![]() auf
der Symmetrieachse soll berechnet werden. Wir verwenden, dass
auf
der Symmetrieachse soll berechnet werden. Wir verwenden, dass
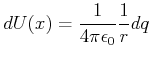
ist, mit
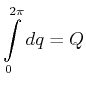
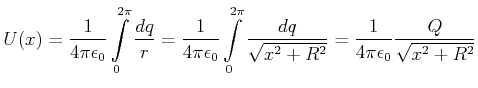 |
(2.54) |
![\includegraphics[width=0.8\textwidth]{kreisringpot}](img400.gif)
Potential eines Kreisringes entlang der Symmetrieachse für eine positive Ladung
|
Analog kann das Potential einer homogen geladenen Scheibe mit dem Radius ![]() entlang ihrer Symmetrieachse
entlang ihrer Symmetrieachse ![]() berechnet werden. Die Ladungsdichte der Scheibe sei
berechnet werden. Die Ladungsdichte der Scheibe sei
![]() . Ein Kreisring mit dem Radius
. Ein Kreisring mit dem Radius ![]() trägt
die Ladung
trägt
die Ladung
![]() und erzeugt dann das Potential
und erzeugt dann das Potential
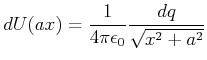 |
(2.55) |
Durch Integration über die gesamte Scheibe erhalten wir
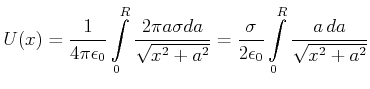 |
(2.56) |
Dieses Integral ergibt nach Bronstein[BSMM00, Seite 309, Nr. 193]
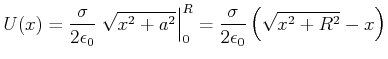 |
(2.57) |
Asymptotisch verläuft auch dieses Potential für
![]() wie das Potential einer Punktladung, da
wie das Potential einer Punktladung, da
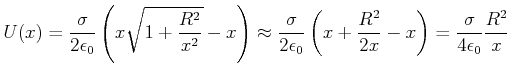
![\includegraphics[width=0.8\textwidth]{kreispot}](img410.gif)
Elektrostatisches Potential einer homogen geladenen Kreisscheibe entlang ihrer Symmetrieachse mit
|
Eine homogen mit der Flächenladungsdichte ![]() geladene Ebene erzeugt ein konstantes elektrisches Feld
geladene Ebene erzeugt ein konstantes elektrisches Feld
![]() . Das elektrostatische Potential eines Punktes
. Das elektrostatische Potential eines Punktes ![]() im Abstand
im Abstand ![]() von der Platte kann
gefunden werden, indem wir entlang des Lots vom Punkt
von der Platte kann
gefunden werden, indem wir entlang des Lots vom Punkt ![]() auf die Ebene integrieren.
auf die Ebene integrieren.
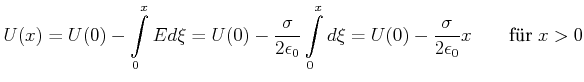 |
(2.58) |
Für ![]() berechnet man
berechnet man
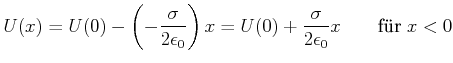 |
(2.59) |
![\includegraphics[width=0.8\textwidth]{ebenepot}](img417.gif)
Potential senkrecht zu einer homogen geladenen Ebene mit
|
Das Potential einer homogen geladenen Kugelschale wird mit dem elektrischen Feld berechnet. Das radiale
elektrische Feld ist
![]() . Damit ist das Potential
. Damit ist das Potential
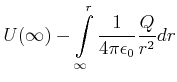 |
|||
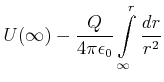 |
|||
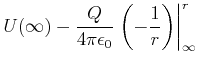 |
|||
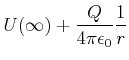 |
(2.60) |
Oder mit
![]()
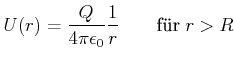 |
(2.61) |
Innerhalb der Kugelschale ist das elektrische Feld null, das Potential also konstant.
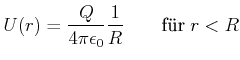 |
(2.62) |
![\includegraphics[width=0.8\textwidth]{kugelschalepot}](img428.gif)
Potential einer homogen geladenen Kugelschale mit
|
Schliesslich berechnen wir das elektrostatische Potential in der Nähe einer unendlich ausgedehnten Linienladung
mit der Ladungsdichte ![]() . Das radiale elektrische Feld ist
. Das radiale elektrische Feld ist
![]() . Das Potential
ist dann
. Das Potential
ist dann
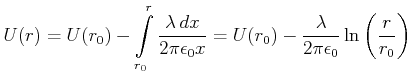 |
(2.63) |
Wir setzen
![]() und erhalten
und erhalten
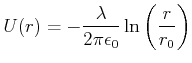 |
(2.64) |
![\includegraphics[width=0.7\textwidth]{linienpot}](img435.gif)
Potential in der Nähe einer unendlich ausgedehnten homogenen Linienladung mit
|
