|
|
Materialien
Folien zur Vorlesung vom 18. 11. 2004: PDF |

| Dieser Stoff wurde am 18. 11. 2004 behandelt |
|
|
Materialien
Folien zur Vorlesung vom 18. 11. 2004: PDF |
|
|
Wir wollen das folgende Problem lösen:
Wir wissen:
Im Inneren der Leiter ist
![]() und
und
![]()
![\includegraphics[width=0.7\textwidth]{elektrostatik-012}](img460.gif)
Integrationsoberfläche an der Grenze Metall-Vakuum.
|
Wir betrachten eine kleine zylinderförmige Oberfläche und verwenden
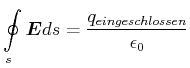 |
(2.73) |
Da das Feld im Inneren des Leiters verschwindet und die Seitenflächen keinen Beitrag geben, ist
| (2.74) |
Bei einer genügend grossen ebenen Fläche ![]() ist die Ladung dann
ist die Ladung dann
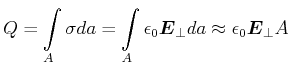 |
(2.75) |
![]() repräsentiert hier die Geometrie, so dass man schliessen kann, dass die gesamte Ladung von der
Geometrie der Leiter abhängt[Jac75, 48]. Wenn wir die Leiter
repräsentiert hier die Geometrie, so dass man schliessen kann, dass die gesamte Ladung von der
Geometrie der Leiter abhängt[Jac75, 48]. Wenn wir die Leiter
![]() betrachten, ist
betrachten, ist
mit ![]() dem Potential auf dem Leiter
dem Potential auf dem Leiter ![]() und
und ![]() dem Potential auf dem Leiter
dem Potential auf dem Leiter ![]() .
. ![]() ist die
Kapazität zwischen den Leitern
ist die
Kapazität zwischen den Leitern ![]() und
und ![]() .
.
Da die Nummerierung in der Gleichung (2.76) willkürlich ist, muss
![]() gelten.
gelten.
Die Einheit der Kapazität ist
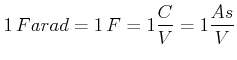 |
(2.77) |
Als erstes Beispiel betrachten wir den Plattenkondensator
![\includegraphics[width=0.3\textwidth]{elektrostatik-013}](img471.gif)
Geometrie eines Plattenkondensators. Wir betrachten auf beiden Seiten eine Fläche
|
Wir benutzen, dass das elektrische Feld einer unendlich ausgedehnten homogenen Flächenladung konstant
![]() ist (Gleichung (2.29) ).
ist (Gleichung (2.29) ).
Auf den Kondensatorplatten ist die Ladung
![]() .
.
Das elektrische Feld zwischen den beiden Platten stammt von beiden Platten, also ist
| (2.78) |
Also ist
![]() . Deshalb ist das Potential am Ort der zweiten Platte gemessen von der ersten
Platte
. Deshalb ist das Potential am Ort der zweiten Platte gemessen von der ersten
Platte
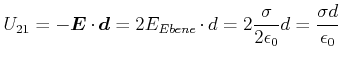 |
(2.79) |
Damit ist die Potentialdifferenz zwischen den beiden Platten oder die angelegte Spannung
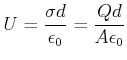 |
(2.80) |
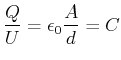 |
(2.81) |
![\includegraphics[width=0.7\textwidth]{elektrostatik-032}](img479.gif)
|
Beispiel: Ein Kondensator mit
![]() ,
, ![]() und
und ![]()
Dann ist
![]() ,
, ![]() ,
,
![]() und
und
![]()
Aus der Additivität des elektrischen Feldes folgt, dass bei der Parallelschaltung von Kondensatoren sich die Kapazitäten addieren.
|
|
![\includegraphics[width=0.6\textwidth]{elektrostatik-014}](img487.gif)
Parallelschaltung von Kondensatoren.
|
| (2.82) |
| (2.83) |
oder
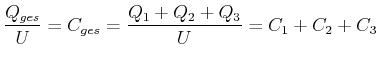 |
(2.84) |
Bei der Reihenschaltung wird die
angelegte Spannung ![]() auf die in Reihe geschalteten Kondensatoren aufgeteilt.
auf die in Reihe geschalteten Kondensatoren aufgeteilt.
![\includegraphics[width=0.6\textwidth]{elektrostatik-015}](img497.gif)
Reihenschaltung oder Serienschaltung von Kondensatoren.
|
Auf den Kondensatoren sind die Ladungen
![]() gespeichert, da in
diesem System nur Ladungen verschoben, aber nicht erzeugt oder vernichtet werden können.
gespeichert, da in
diesem System nur Ladungen verschoben, aber nicht erzeugt oder vernichtet werden können.
Also ist
| (2.86) |
oder
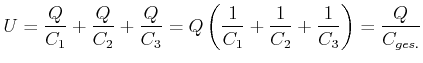 |
(2.87) |
