|
|

| Dieser Stoff wurde am 02. 12. 2004 behandelt |
|
|
Die Energiedichte im Kondensator ist
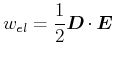 |
(2.128) |
![\includegraphics[width=0.6\textwidth]{elektrostatik-021}](img619.gif)
Links eine dielektrische Flüssigkeit im Kondensator ohne angelegtes Feld. Rechts mit angelegtem Feld.
|
Wenn wir das obige Experiment durchführen, steigt die dielektrische Flüssigkeit. Dabei erhöht sich die im elektrischen Feld gespeicherte Energie und auch die potentielle Energie.
Wie geht das?
![\includegraphics[width=0.8\textwidth]{elektrostatik-022}](img620.gif)
Skizze der Änderungen beim Anlegen einer Spannung
|
Zur Berechnung müssen wir auch die Batterie oder Spannungsquelle mit betrachten[Kän78].
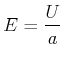
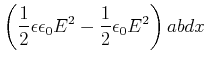 |
|||
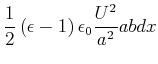 |
|||
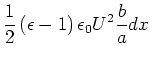 |
(2.129) |
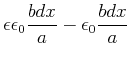 |
|||
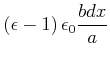 |
(2.130) |
| (2.131) | |||
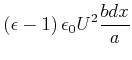 |
| (2.132) |
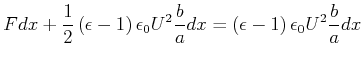 |
(2.133) |
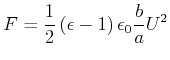 |
(2.134) |
