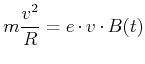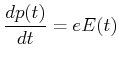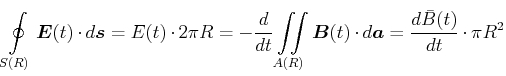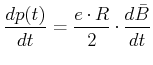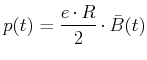




Next: Skin-Effekt
Up: Das Faradaysche Induktionsgesetz
Previous: Elektromotoren
Contents
Index
| Dieser Stoff wurde am 3. 2. 2005
behandelt |
Die Idee hinter der Konstruktion des Betatrons ist, dass bei einem zeitabhängigen 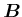 -Feld nach
-Feld nach
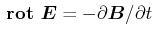 auch ein zeitabhängiges
auch ein zeitabhängiges 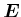 -Feld existiert.
-Feld existiert.
Nach dem Induktionsgesetz
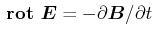 hat das durch ein in die
hat das durch ein in die 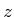 -Richtung
zeigende Magnetfeld induzierte elektrische Feld keine
-Richtung
zeigende Magnetfeld induzierte elektrische Feld keine 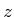 -Komponente. Nehmen wir an, dass das
-Komponente. Nehmen wir an, dass das 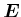 -Feld eine
Radialkomponente hätte. Sie könnte zum Beispiel in die
-Feld eine
Radialkomponente hätte. Sie könnte zum Beispiel in die 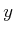 -Richtung zeigen. Rotieren wir die ganze Anordnung um
-Richtung zeigen. Rotieren wir die ganze Anordnung um
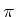 um die
um die 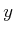 -Achse und kehren die Richtung des
-Achse und kehren die Richtung des 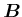 -Feldes um, haben wir wieder die Ausgangsanordnung.
Mit der Richtungsumkehr von
-Feldes um, haben wir wieder die Ausgangsanordnung.
Mit der Richtungsumkehr von 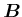 hat aber auch
hat aber auch 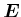 die Richtung geändert (Induktionsgesetz). Dies ist
aber im Widerspruch zur Ausgangssituation. Deshalb kann es kein radiales
die Richtung geändert (Induktionsgesetz). Dies ist
aber im Widerspruch zur Ausgangssituation. Deshalb kann es kein radiales 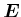 -Feld geben: das
-Feld geben: das 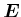 -Feld
ist tangential und beschleunigt die geladenen Teilchen. Damit die Teilchen auf der Kreisbahn bleiben, muss
-Feld
ist tangential und beschleunigt die geladenen Teilchen. Damit die Teilchen auf der Kreisbahn bleiben, muss
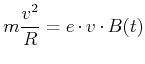 |
(4.384) |
oder
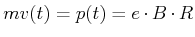 |
(4.385) |
Das zweite Newtonsche Axiom in tangentialer Richtung angewandt bedeutet
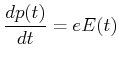 |
(4.386) |
Mit der Integralform des Induktionsgesetzes erhält man mit einer stationären Kreisbahn 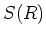 mit dem Radius
mit dem Radius 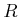
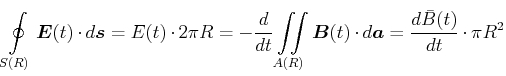 |
(4.387) |
wobei 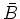 das über die Fläche des Kreises gemittelte
das über die Fläche des Kreises gemittelte 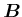 -Feld ist. Durch Kombination der obigen
Gleichungen und unter Berücksichtigung der Vorzeichen erhalten wir
-Feld ist. Durch Kombination der obigen
Gleichungen und unter Berücksichtigung der Vorzeichen erhalten wir
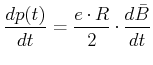 |
(4.388) |
Die Integration mit den Anfangsbedingungen 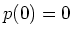 und
und 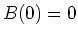 liefert
liefert
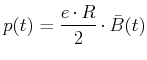 |
(4.389) |
Der Vergleich mit der Bedingung für die Zentripetalkraft liefert die Wideroe-Bedingung
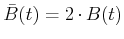 |
(4.390) |
Diese Bedingung kann durch eine geeignete Wahl der Form der Polschuhe erreicht werden.





Next: Skin-Effekt
Up: Das Faradaysche Induktionsgesetz
Previous: Elektromotoren
Contents
Index
Marti
2011-10-13

![]() -Feld nach
-Feld nach
![]() auch ein zeitabhängiges
auch ein zeitabhängiges ![]() -Feld existiert.
-Feld existiert.
![\includegraphics[width=0.7\textwidth]{magnetismus-016}](img1251.gif)
![]() hat das durch ein in die
hat das durch ein in die ![]() -Richtung
zeigende Magnetfeld induzierte elektrische Feld keine
-Richtung
zeigende Magnetfeld induzierte elektrische Feld keine ![]() -Komponente. Nehmen wir an, dass das
-Komponente. Nehmen wir an, dass das ![]() -Feld eine
Radialkomponente hätte. Sie könnte zum Beispiel in die
-Feld eine
Radialkomponente hätte. Sie könnte zum Beispiel in die ![]() -Richtung zeigen. Rotieren wir die ganze Anordnung um
-Richtung zeigen. Rotieren wir die ganze Anordnung um
![]() um die
um die ![]() -Achse und kehren die Richtung des
-Achse und kehren die Richtung des ![]() -Feldes um, haben wir wieder die Ausgangsanordnung.
Mit der Richtungsumkehr von
-Feldes um, haben wir wieder die Ausgangsanordnung.
Mit der Richtungsumkehr von ![]() hat aber auch
hat aber auch ![]() die Richtung geändert (Induktionsgesetz). Dies ist
aber im Widerspruch zur Ausgangssituation. Deshalb kann es kein radiales
die Richtung geändert (Induktionsgesetz). Dies ist
aber im Widerspruch zur Ausgangssituation. Deshalb kann es kein radiales ![]() -Feld geben: das
-Feld geben: das ![]() -Feld
ist tangential und beschleunigt die geladenen Teilchen. Damit die Teilchen auf der Kreisbahn bleiben, muss
-Feld
ist tangential und beschleunigt die geladenen Teilchen. Damit die Teilchen auf der Kreisbahn bleiben, muss