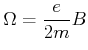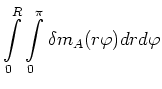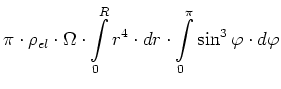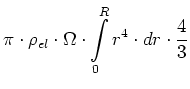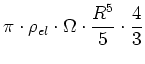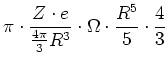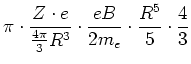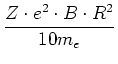




Next: Magnetisierung
Up: Magnetische Eigenschaften der Materie
Previous: Der Satz von Larmor
Contents
Index
| Dieser Stoff wurde am 10. 2. 2005
behandelt |
|
Berechnung des Diamagnetismus
|
Im diamagnetischen Atom ist die Summe aller magnetischer Momente der Elektronen exakt null.
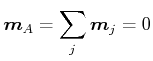 |
(4.423) |
Man kann sich dies vereinfacht so vorstellen, dass jede Elektronenbahn von zwei gegenläufigen Elektronen besetzt
ist. Ein diamagnetisches Atom hat deshalb, ohne äusseres 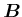 -Feld eine kugelsymmetrische Ladungsverteilung.
Diese entsteht, weil sich die einzelnen Elektronenbewegungen über die Zeit ausmitteln.
-Feld eine kugelsymmetrische Ladungsverteilung.
Diese entsteht, weil sich die einzelnen Elektronenbewegungen über die Zeit ausmitteln.
Wenn ein 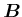 -Feld eingeschaltet wird, beginnt diese kugelsymmetrische Ladungsverteilung mit der
Larmorfrequenz zu präzedieren. Durch diese Präzession im Magnetfeld entsteht ein von null verschiedenes
magnetisches Moment
-Feld eingeschaltet wird, beginnt diese kugelsymmetrische Ladungsverteilung mit der
Larmorfrequenz zu präzedieren. Durch diese Präzession im Magnetfeld entsteht ein von null verschiedenes
magnetisches Moment 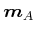 , das zum Diamagnetismus führt. Zur vereinfachten Berechnung nimmt man an, dass das
Atom eine homogen geladene Kugel ist mit der Ladungsdichte
, das zum Diamagnetismus führt. Zur vereinfachten Berechnung nimmt man an, dass das
Atom eine homogen geladene Kugel ist mit der Ladungsdichte
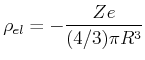 |
(4.424) |
wobei 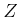 die Kernladungszahl und
die Kernladungszahl und 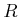 der Radius der Elektronenwolke ist.
der Radius der Elektronenwolke ist.
Diese homogen geladene Kugel rotiert im äusseren Magnetfeld mit
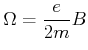 |
(4.425) |
Durch ein raumfestes Flächenelement fliesst der Strom
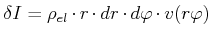 |
(4.426) |
mit
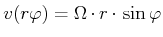 |
(4.427) |
Da die Ladungen negativ sind, ist das magnetische Moment 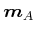 entgegengesetzt zu
entgegengesetzt zu
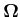 und entgegengesetzt zu
und entgegengesetzt zu 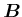 , hier also nach unten, gerichtet. Dieses magnetische Moment ist
, hier also nach unten, gerichtet. Dieses magnetische Moment ist
 |
(4.428) |
oder
Der Betrag des gesamten magnetischen Momentes erhält man durch Integration über 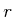 und
und 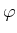 Er ist
Er ist
Vektoriell geschrieben erhalten wir für das diamagnetische Moment
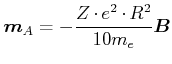 |
(4.431) |
Diese diamagnetische Moment ist in allen Atomen vorhanden. Bei paramagnetischen und ferromagnetischen
Substanzen wird es unterdrückt.

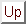




Next: Magnetisierung
Up: Magnetische Eigenschaften der Materie
Previous: Der Satz von Larmor
Contents
Index
Marti
2011-10-13
![\includegraphics[width=0.7\textwidth]{magnetismus-024}](img1327.gif)

![\includegraphics[width=0.7\textwidth]{magnetismus-024}](img1327.gif)
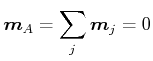
![]() -Feld eingeschaltet wird, beginnt diese kugelsymmetrische Ladungsverteilung mit der
Larmorfrequenz zu präzedieren. Durch diese Präzession im Magnetfeld entsteht ein von null verschiedenes
magnetisches Moment
-Feld eingeschaltet wird, beginnt diese kugelsymmetrische Ladungsverteilung mit der
Larmorfrequenz zu präzedieren. Durch diese Präzession im Magnetfeld entsteht ein von null verschiedenes
magnetisches Moment ![]() , das zum Diamagnetismus führt. Zur vereinfachten Berechnung nimmt man an, dass das
Atom eine homogen geladene Kugel ist mit der Ladungsdichte
, das zum Diamagnetismus führt. Zur vereinfachten Berechnung nimmt man an, dass das
Atom eine homogen geladene Kugel ist mit der Ladungsdichte
![\includegraphics[width=0.3\textwidth]{magnetismus-025}](img1331.gif)