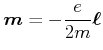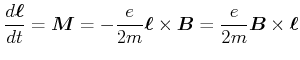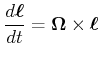




Next: Diamagnetismus
Up: Magnetische Eigenschaften der Materie
Previous: Kugeln im inhomogenen Magnetfeld
Contents
Index
| Dieser Stoff wurde am 10. 2. 2005
behandelt |
(Siehe Leisi, Klassische Physik II [Lei98, pp. 162])
|
Illustration zum Satz von Larmor
|
Wir hatten postuliert, dass das Verhalten der Materie in einem Gradienten eines Magnetfeldes durch atomare
Kreisströme gegeben ist. Wenn wir ein Modell (nach der Quantenphysik nicht realistisch) eines Atoms betrachten,
bei dem ein einzelnes Elektron auf einer Bahn mit dem Radius 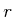 sich um den positiv geladenen Kern bewegt, ist
der resultierende Strom
sich um den positiv geladenen Kern bewegt, ist
der resultierende Strom
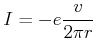 |
(4.405) |
Der Betrag des magnetischen Momentes ist dann
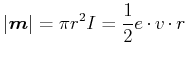 |
(4.406) |
Die Wirkung eines äusseren Magnetfeldes wird berechnet, indem man betrachtet, wie ein einzelnes Atom auf ein von
null anwachsendes äusseres Feld reagiert.
|
Langsames Einschalten eines Magnetfeldes für ein Elektron in einem Atom. Im linken Schaubild sind die
positiven Richtungen definiert.
|
Im Ausgangszustand ist die Zentripetalkraft
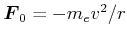 die Coulombanziehung zwischen dem Elektron und
dem Kern sowie durch die gemittelte Coulombabstossung durch die anderen Elektronen gegeben. Das anwachsende
Magnetfeld hat die gleiche Wirkung wie beim Betatron: es entsteht ein tangentiales
die Coulombanziehung zwischen dem Elektron und
dem Kern sowie durch die gemittelte Coulombabstossung durch die anderen Elektronen gegeben. Das anwachsende
Magnetfeld hat die gleiche Wirkung wie beim Betatron: es entsteht ein tangentiales 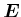 -Feld, das das
Elektron beschleunigt. Wir setzen die
-Feld, das das
Elektron beschleunigt. Wir setzen die 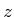 -Achse nach oben an. In einem rechtshändigen System ist dann
-Achse nach oben an. In einem rechtshändigen System ist dann
- das Magnetfeld:
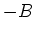 , Betrag:
, Betrag: 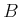
- die Geschwindigkeit:
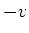 , Betrag:
, Betrag: 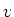
- die Zentripetalkraft:
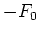 , Betrag:
, Betrag: 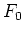
- das induzierte elektrische Feld:
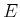 , Betrag:
, Betrag: 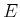
Wir setzen diese Grössen ein, um vorzeichenrichtig zu rechnen. Aus dem Induktionsgesetz
folgt
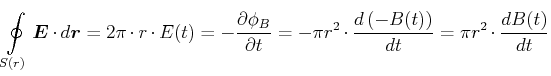 |
(4.407) |
Dabei ist
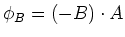 Wir erhalten also
Wir erhalten also
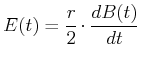 |
(4.408) |
Die Beschleunigung des Elektrons (nicht-relativistisch) ist durch das zweite Newtonsche Axiom gegeben
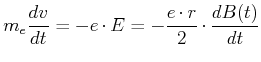 |
(4.409) |
Hier ist 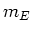 die Ruhemasse des Elektrons. Die Geschwindigkeitsänderung hängt also mit der Magnetfeldänderung wie
folgt zusammen
die Ruhemasse des Elektrons. Die Geschwindigkeitsänderung hängt also mit der Magnetfeldänderung wie
folgt zusammen
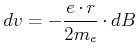 |
(4.410) |
Der gesamte Geschwindigkeitszuwachs des Elektrons ist also
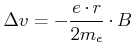 |
(4.411) |
wenn 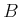 das Feld im Endzustand ist. Der Betrag der Geschwindigkeit hat also zugenommen. Nun bewirkt das äussere
das Feld im Endzustand ist. Der Betrag der Geschwindigkeit hat also zugenommen. Nun bewirkt das äussere
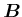 -Feld die Lorentzkraft
-Feld die Lorentzkraft
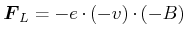 |
(4.412) |
die, nach der rechten Hand-Regel zum Kreiszentrum zeigt. Die Zentripetalkraft ist im Endzustand durch
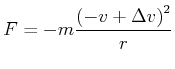 |
(4.413) |
Da
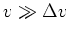 ist, können wir nach Taylor entwickeln
ist, können wir nach Taylor entwickeln
Die Lorentz-Kraft bewirkt also, dass die Elektronenbahnen für kleine Geschwindigkeitsänderungen sich nicht ändern.
Die Larmorwinkelgeschwindigkeit ist
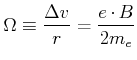 |
(4.415) |
und vektoriell geschrieben
Larmorwinkelgeschwindigkeit
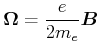 |
(4.416) |
In einem mit der Winkelgeschwindigkeit
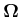 rotierenden System sind die Elektronenbahnen im Atom
unverändert. rotierenden System sind die Elektronenbahnen im Atom
unverändert.
|
Der Satz von Larmor gilt allgemein, auch bei beliebiger Orientierung von Magnetfeld
und Bahnebene des Elektrons. Der Satz von Larmor bildet die Grundlage des Verständnisses des Diamagnetismus
|
Berechnung der Larmorfrequenz mit einem Kreisel
|
Man kann den Satz von Larmor aus der Kreiseltheorie ableiten. Das Elektron ist, bei einer Bahn mit
konstantem Radius, ein starrer Körper. Dieser Kreisel hat den Drehimpuls
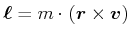 |
(4.417) |
Das magnetische Moment des Kreisstromes ist nach Gleichung (4.110)
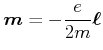 |
(4.418) |
Der Kreisel erfährt ein mechanisches Drehmoment
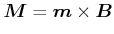 |
(4.419) |
Der Drehimpulssatz bedeutet, dass
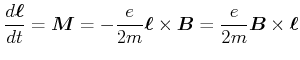 |
(4.420) |
Wir erhalten also eine Präzessionsbewegung des Drehimpuslvektors
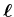 um
um 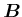 mit der
Winkelgeschwindigkeit
mit der
Winkelgeschwindigkeit
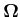
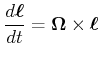 |
(4.421) |
Wir erhalten die
vektorielle Schreibweise der Larmorfrequenz
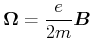 |
(4.422) |
|





Next: Diamagnetismus
Up: Magnetische Eigenschaften der Materie
Previous: Kugeln im inhomogenen Magnetfeld
Contents
Index
Marti
2011-10-13
![\includegraphics[width=0.7\textwidth]{magnetismus-021}](img1293.gif)

![\includegraphics[width=0.7\textwidth]{magnetismus-021}](img1293.gif)
![]() sich um den positiv geladenen Kern bewegt, ist
der resultierende Strom
sich um den positiv geladenen Kern bewegt, ist
der resultierende Strom
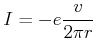
![\includegraphics[width=0.9\textwidth]{magnetismus-022}](img1296.gif)
![]() die Coulombanziehung zwischen dem Elektron und
dem Kern sowie durch die gemittelte Coulombabstossung durch die anderen Elektronen gegeben. Das anwachsende
Magnetfeld hat die gleiche Wirkung wie beim Betatron: es entsteht ein tangentiales
die Coulombanziehung zwischen dem Elektron und
dem Kern sowie durch die gemittelte Coulombabstossung durch die anderen Elektronen gegeben. Das anwachsende
Magnetfeld hat die gleiche Wirkung wie beim Betatron: es entsteht ein tangentiales ![]() -Feld, das das
Elektron beschleunigt. Wir setzen die
-Feld, das das
Elektron beschleunigt. Wir setzen die ![]() -Achse nach oben an. In einem rechtshändigen System ist dann
-Achse nach oben an. In einem rechtshändigen System ist dann
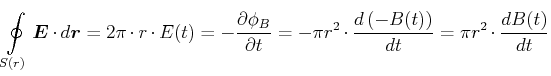
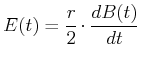
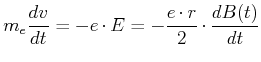
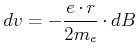
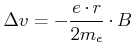
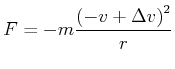
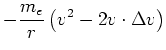
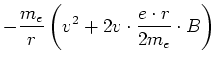
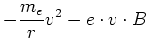
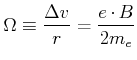
![\includegraphics[width=0.5\textwidth]{magnetismus-023}](img1320.gif)