




Next: Ferromagnetismus
Up: Magnetische Eigenschaften der Materie
Previous: Das magnetische Moment des
Contents
Index
| Dieser Stoff wurde am 10. 2. 2005
behandelt |
(Siehe Kneubühl, Repetitorium der
Physik [Kne74, pp. 262])
Bei paramagnetischen Atomen hebt sich das magnetische Bahnmoment der einzelnen Elektronen eines Atoms sowie deren
von den Spins herrührendes magnetisches Moment nicht vollständig auf.
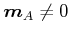 |
(4.441) |
Das magnetische Moment eines paramagnetischen Atoms hat die Grössenordnung eines Bohrsche Magneton 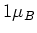 . Ohne
äusseres Magnetfeld verschwindet die makroskopische Magnetisierung, da die einzelnen atomaren magnetischen Momente
ungeordnet sind. Im äusseren Magnetfeld ordnen sich die magnetischen Momente teilweise, da die thermische
Brownsche Bewegung, temperaturabhängig, für Unordnung sorgt.
. Ohne
äusseres Magnetfeld verschwindet die makroskopische Magnetisierung, da die einzelnen atomaren magnetischen Momente
ungeordnet sind. Im äusseren Magnetfeld ordnen sich die magnetischen Momente teilweise, da die thermische
Brownsche Bewegung, temperaturabhängig, für Unordnung sorgt.
Die Magnetisierung kann mit der folgenden Überlegung berechnet werden. Wir setzen an
Die Energie des magnetischen Dipols 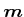 im Magnetfeld
im Magnetfeld 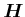 hängt nur von
hängt nur von 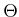 ab. Wir machen eine
Koordinatentransformation auf
ab. Wir machen eine
Koordinatentransformation auf
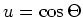 . Die Energie ist dann
. Die Energie ist dann
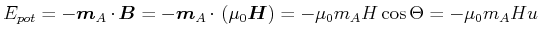 |
(4.443) |
Die Magnetisierung 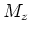 in der
in der 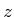 -Richtung, der Richtung des Magnetfeldes
-Richtung, der Richtung des Magnetfeldes 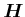 , ist
, ist
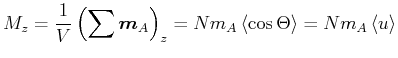 |
(4.444) |
Bei endlichen Temperaturen müssen die potentiellen Energien 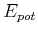 nach der Boltzmannstatistik
verteilt sein, also
nach der Boltzmannstatistik
verteilt sein, also
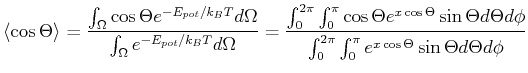 |
(4.445) |
mit
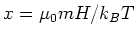 . In der Koordinate
. In der Koordinate 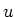 und nach ausführen der trivialen Integration über
und nach ausführen der trivialen Integration über 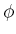 lautet die
Gleichung
lautet die
Gleichung
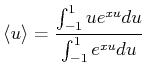 |
(4.446) |
Wir wechseln auf
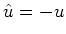 und erhalten
und erhalten
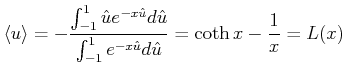 |
(4.447) |
wobei 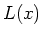 die Langevin-Funktion ist. Also ist
die Langevin-Funktion ist. Also ist
Diese klassisch berechnete Magnetisierung ist für kleine Magnetfelder, also
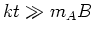 verifizierbar. Da für
verifizierbar. Da für
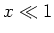 die Reihenentwicklung
die Reihenentwicklung
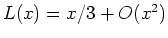 gilt bekommen wir das Curie-Gesetz
gilt bekommen wir das Curie-Gesetz
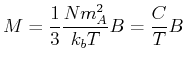 |
(4.449) |
Hier ist 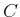 die Curie-Konstante
die Curie-Konstante
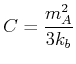 |
(4.450) |
Schematischer Verlauf der Magnetisierung (Curie-Gesetz für kleine 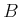 ). ). 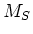 ist die
Sättigungsmagnetisierung. ist die
Sättigungsmagnetisierung.
|





Next: Ferromagnetismus
Up: Magnetische Eigenschaften der Materie
Previous: Das magnetische Moment des
Contents
Index
Marti
2011-10-13

![]() im Magnetfeld
im Magnetfeld ![]() hängt nur von
hängt nur von ![]() ab. Wir machen eine
Koordinatentransformation auf
ab. Wir machen eine
Koordinatentransformation auf
![]() . Die Energie ist dann
. Die Energie ist dann
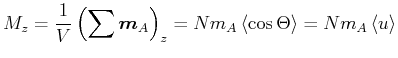
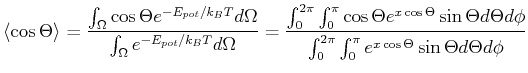
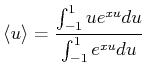
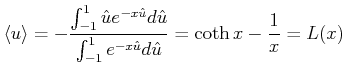
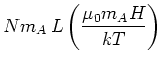
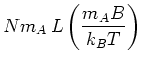
![$\displaystyle Nm_A\left[\coth\left(\frac{m_A B}{k_BT}\right)-\frac{k_BT}{m_A B}\right]$](img1391.gif)
![]() verifizierbar. Da für
verifizierbar. Da für
![]() die Reihenentwicklung
die Reihenentwicklung
![]() gilt bekommen wir das Curie-Gesetz
gilt bekommen wir das Curie-Gesetz
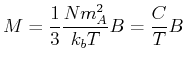
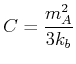
![\includegraphics[width=0.7\textwidth]{magnetismus-028}](img1397.gif)
