|
|
Materialien
Folien zur Vorlesung vom 17. 02. 2005: PDF |

| Dieser Stoff wurde am 17. 2. 2005 behandelt |
|
|
Materialien
Folien zur Vorlesung vom 17. 02. 2005: PDF |
(Siehe Leisi, Klassische Physik II [Lei98, pp. 251])
Maxwellgleichungen werden gebraucht, um die Funktionsweise von
|
Bis jetzt kennen wir die folgenden Gleichungen um die elektrischen Phänomene zu beschreiben:
| Gausssches Gesetz |
|
|
I | |
| Induktionsgesetz |
|
|
II | |
| Quellenfreiheit |
|
0 | III | |
| Durchflutungsgesetz |
|
|
IV |
Zusätzlich zu den obigen Gleichungen muss die Kontinuitätsgleichung für Ladungen gelten
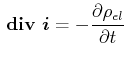 |
(5.455) |
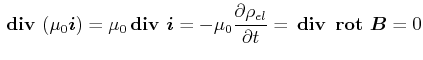 |
(5.456) |
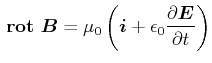 |
(5.457) |
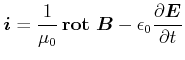 |
(5.458) |
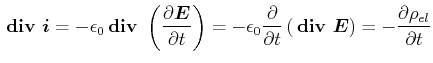 |
(5.459) |
genannt.
Zusammen mit dem Kraftgesetz
| (5.461) |
| Die Maxwellsche Verschiebungsstromdichte, die eingeführt wurde um die Maxwellgleichungen mit der Kontinuitätsgleichung kompatibel zu machen, führt dazu, dass man aus den Maxwellgleichungen elektromagnetische Wellen vorhersagen kann. |
| Die Maxwellgleichungen sind nicht invariant unter der Galilei-Transformation. Diese Beobachtung war ein wichtiger Meilenstein auf dem Weg zur speziellen Relativitätstheorie. |
Die Integralform des modifizierten Durchflutungsgesetzes ist
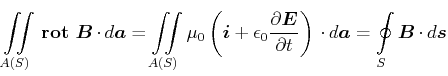 |
(5.462) |
Das Gausssche Gesetz liefert
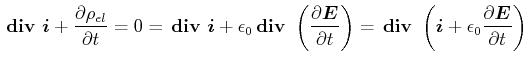 |
(5.464) |
Die Integralformeln der Maxwellgleichungen lauten
|
Der Unterschied zwischen der zweiten und der dritten Maxwellgleichung ist, dass in der zweiten Gleichung über eine
einfache, von der Kurve ![]() aufgespannte Fläche
aufgespannte Fläche ![]() integriert wird, während in der dritten Gleichung über die
das Volumen
integriert wird, während in der dritten Gleichung über die
das Volumen ![]() einschliessende Fläche
einschliessende Fläche ![]() integriert wird.
integriert wird.
Für Medien mit tensoriellen Eigenschaften benötigt man die beiden Materialgleichungen
| (5.466) | |||
Die Maxwellgesetze für allgemeine Materialien lauten
| (5.467) | |||
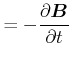 |
|||
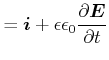 |
in der differentiellen Schreibweise und
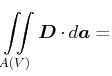 |
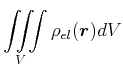 |
(5.468) | |
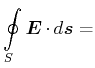 |
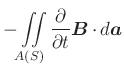 |
||
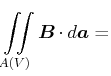 |
|||
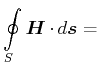 |
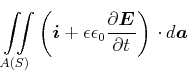 |
in der Integralschreibweise.
Anwendung
Wir betrachten einen langen kreiszylindrischen Leiter mit dem Durchmesser ![]() , aus dem eine Scheibe mit der Dicke
, aus dem eine Scheibe mit der Dicke
![]() herausgeschnitten wurde. Dieser Leiter werde an eine Gleichstromquelle mit
herausgeschnitten wurde. Dieser Leiter werde an eine Gleichstromquelle mit
![]() angeschlossen.
Die Endflächen beim herausgeschnittenen Stück wirken wie ein Kondensator. Also ist
angeschlossen.
Die Endflächen beim herausgeschnittenen Stück wirken wie ein Kondensator. Also ist
| (5.469) |
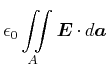 |
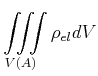 |
(5.470) | |
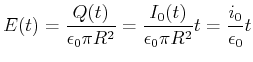 |
(5.471) |
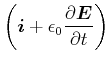
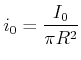 |
(5.472) |
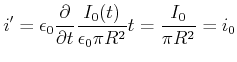 |
(5.473) |
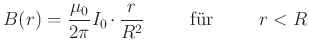 |
(5.474) |
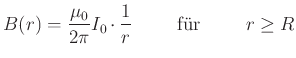 |
(5.475) |
