Weiter: Eigenschaften des B-Feldes Oben: Elektrische Ströme Zurück: Magnetfeld und Lorentzkraft Skript: PDF-Datei Übungen: Blätter
(Siehe Tipler, Physik [TM04, pp. 812]) (Siehe Leisi, Klassische Physik II [Lei98, pp. 91])
Um die Magnetische Kraft zu berechnen gehen wir in zwei Schritten vor:
(Siehe Leisi, Klassische Physik II [Lei98, pp. 91])
![\includegraphics[width=0.6\textwidth]{strom-003}](img815.gif)
Metallischer Gastank mit Ausströmöffnung.
|
Mit zwei Gedankenexperimenten soll geklärt werden, ob die Ladung von der Geschwindigkeit abhängt. Zuerst
schliessen wir eine grosse Menge ![]() -Gas in den metallischen Tank ein, entladen ihn, und lassen das Gas
ausströmen. Die Ladung des leeren Tanks ist unmessbar klein. Daraus schliesst man:
-Gas in den metallischen Tank ein, entladen ihn, und lassen das Gas
ausströmen. Die Ladung des leeren Tanks ist unmessbar klein. Daraus schliesst man:
mit einer Genauigkeit von |
Dies folgt aus dem Gaussschen Gesetz Gleichung (2.14)
![$\displaystyle \int\!\!\!\int\limits_{A} \vec{E}\cdot d\vec{a}= 0\pm a\vert q_{Elektron}\vert = \frac{1}{\epsilon_0}\left[NQ(H_2)+q\right]$](img819.gif) |
(3.210) |
Der Versuch wird mit ![]() -Gas wiederholt. Das Resultat ist das gleiche. Nun bewegen sich aber die zwei Protonen im
-Gas wiederholt. Das Resultat ist das gleiche. Nun bewegen sich aber die zwei Protonen im
![]() -Atom mit sehr grosser Geschwindigkeit. Das bedeutet, dass die Ladung des Protons
unabhängig von der Geschwindigkeit ist. Die Ladung muss insbesondere in jedem Inertialsystem
gleich sein. Wir betrachten zwei Inertialsysteme
-Atom mit sehr grosser Geschwindigkeit. Das bedeutet, dass die Ladung des Protons
unabhängig von der Geschwindigkeit ist. Die Ladung muss insbesondere in jedem Inertialsystem
gleich sein. Wir betrachten zwei Inertialsysteme ![]() und
und ![]() 9
9
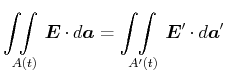 |
(3.211) |
(Siehe Leisi, Klassische Physik II [Lei98, pp. 94])
Den Strom ![]() modellieren wir mit zwei Ketten aus Ladungsträgern, je eine positiv und negativ geladen. Ihre
Linienladungsdichten
modellieren wir mit zwei Ketten aus Ladungsträgern, je eine positiv und negativ geladen. Ihre
Linienladungsdichten ![]() sollen so sein, dass die beiden Ketten neutral sind. Im Ruhesystem
sollen so sein, dass die beiden Ketten neutral sind. Im Ruhesystem ![]() der
positiven Ladungen ist
der
positiven Ladungen ist
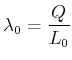 |
(3.212) |
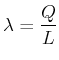 |
(3.213) |
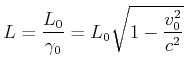 |
(3.214) |
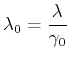 |
(3.215) |
Im Ruhesystem ![]() , in dem das Teilchen mit der Ladung
, in dem das Teilchen mit der Ladung ![]() in Ruhe ist, sieht die Situation anders aus.
Die Geschwindigkeit der positiven und der negativen Ladungsketten ist unterschiedlich. deshalb sind sie zusammen
nicht mehr elektrisch neutral. Auf die Ladung
in Ruhe ist, sieht die Situation anders aus.
Die Geschwindigkeit der positiven und der negativen Ladungsketten ist unterschiedlich. deshalb sind sie zusammen
nicht mehr elektrisch neutral. Auf die Ladung ![]() wirkt eine elektrostatische Kraft. Da die
Relativgeschwindigkeit der positiven Ladungen zu
wirkt eine elektrostatische Kraft. Da die
Relativgeschwindigkeit der positiven Ladungen zu ![]() kleiner ist als die der negativen
Ladungen, liegen in
kleiner ist als die der negativen
Ladungen, liegen in ![]() die positiven Ladungen weniger dicht als die
negativen10.
Die beiden Ladungsketten sind insgesamt negativ geladen. Deshalb wird
die positiven Ladungen weniger dicht als die
negativen10.
Die beiden Ladungsketten sind insgesamt negativ geladen. Deshalb wird ![]() angezogen, wenn
angezogen, wenn ![]() ist. Das
ist. Das
![]() -Feld in die
-Feld in die ![]() -Richtung erzeugt in
-Richtung erzeugt in ![]() die Kraft
die Kraft
| (3.216) |
|
Das |
Das elektrische Feld einer Linienladung im Abstand ![]() ist
ist
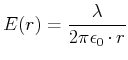 |
(3.217) |
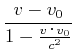 |
|||
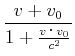 |
(3.218) |
| (3.219) | |||
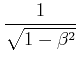 |
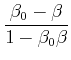 |
(3.220) | ||
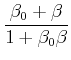 |
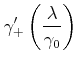 |
(3.221) | ||
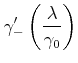 |
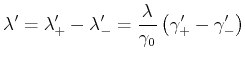 |
(3.222) |
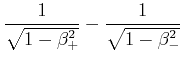 |
(3.223) | ||
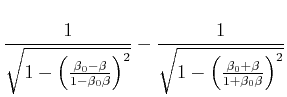 |
|||
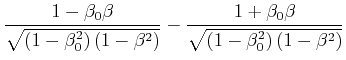 |
|||
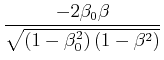 |
|||
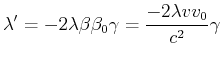 |
(3.224) |
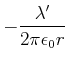 |
(3.225) | ||
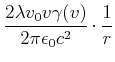 |
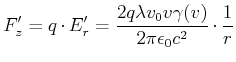 |
(3.226) |
| (3.227) | |||
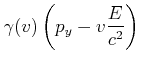 |
|||
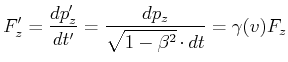 |
(3.228) |
| (3.229) |
Multipliziert man Gleichung (3.96) mit der Dichte der Ladungsträger ![]() , so erhält man die zu
, so erhält man die zu ![]() proportionale Kraft.
proportionale Kraft.
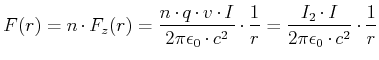 |
(3.231) |
Othmar Marti