![\includegraphics[width=0.7\textwidth]{fotoeffekt-1}](img269.gif)

| Dieser Stoff wurde am 19. 4. 2005 behandelt |
![\includegraphics[width=0.7\textwidth]{fotoeffekt-1}](img269.gif)
|
|
|
Beobachtungen
![\includegraphics[height=0.15\textheight]{fotoeffekt-2}](img270.gif)
![\includegraphics[height=0.15\textheight]{fotoeffekt-3}](img271.gif)
|
![\includegraphics[height=0.17\textheight]{fotoeffekt-4}](img272.gif)
![\includegraphics[height=0.17\textheight]{fotoeffekt-5}](img273.gif)
|
![\includegraphics[width=0.7\textwidth]{fotoeffekt-6}](img274.gif)
![\includegraphics[width=0.7\textwidth]{fotoeffekt-7}](img275.gif)
![\includegraphics[width=0.7\textwidth]{fotoeffekt-8}](img276.gif)
|
Kinetische Energie des Elektrons:
| (4.48) |
![]() ist ausgeschmiert, da die Elektronenverteilung im Festkörper ausgeschmiert ist und da die Elektronen
nicht nur senkrecht emittiert werden.
ist ausgeschmiert, da die Elektronenverteilung im Festkörper ausgeschmiert ist und da die Elektronen
nicht nur senkrecht emittiert werden.
![]() heisst die Austrittsarbeit.
heisst die Austrittsarbeit.
|
|
|
|
| Dieser Stoff wurde am 19. 4. 2005 behandelt |
Lichtdruck[MRH$^+$92]
Der Impuls des Lichtes ist mit der Energie verknüpft.
relativistische Energie-Impuls-Beziehung
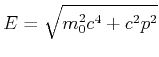
Photon: ![]() und
und
![]()
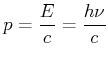 |
(4.49) |
Impulsänderung bei Absorption und Reflexion
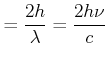 |
(4.50) | ||
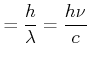 |
Mechanischer Druck
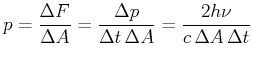
Mit
![]()
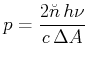
Die Intensität ist
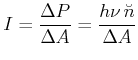
Wir bekommen also
| (4.51) | |||
![\includegraphics[width=0.7\textwidth]{lichtdruck-3}](img295.gif)
|
Klassisch aus Elektrizitätslehre
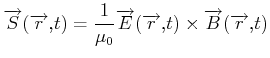
Der Pointingvektor ist gibt den Energiefluss an. Hier ist
![]()
Druck ist Energiedichte. Wenn die Energiedichte ![]() mit der Geschwindigkeit
mit der Geschwindigkeit ![]() wandert, ergibt sich
Pointingvektor
wandert, ergibt sich
Pointingvektor ![]() .
.
und damit der Druck
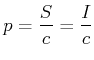 |
(4.52) |
![\includegraphics[width=0.7\textwidth]{lichtdruck}](img302.gif)
|
Dynamische Masse des Photons
Aus
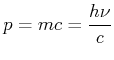
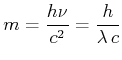 |
(4.53) |
Bsp:
![]() dann ist
dann ist
![]()
| Dieser Stoff wurde am 19. 4. 2005 behandelt |
![\includegraphics[width=0.7\textwidth]{compton}](img308.gif)
|
![\includegraphics[width=0.7\textwidth]{compton-1}](img309.gif)
|
Impulserhaltung
Im Falle kleiner Frequenzverschiebung
![]() bildet dei Mittelsenkrechte mit
bildet dei Mittelsenkrechte mit ![]() und
und ![]() ein rechtwinkliges Dreieck mit
ein rechtwinkliges Dreieck mit ![]() als Hypothenuse.
als Hypothenuse.
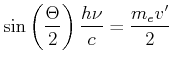 |
(4.54) |
Energieerhaltung
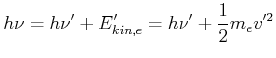 |
(4.55) |
Mit
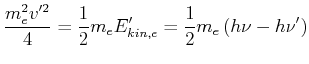
wird
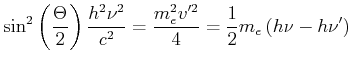
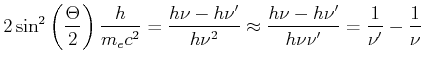
Mit
![]()
| Dieser Stoff wurde am 19. 4. 2005 behandelt |
![\includegraphics[width=0.7\textwidth]{moessbauer1}](img320.gif)
|
Bei der Emission eines ![]() -Quants müssen Energie und Impuls erhalten werden. Sei
-Quants müssen Energie und Impuls erhalten werden. Sei ![]() die Energie eines
die Energie eines
![]() -Quants, wenn der Kern bei der Emission in Ruhe bleibt.
-Quants, wenn der Kern bei der Emission in Ruhe bleibt.
![\includegraphics[width=0.3\textwidth]{moessbauer2}](img321.gif)
|
Impulserhaltung
| (4.58) | |||
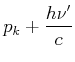 |
Kinetische Energie des Kerns (sei ![]() die Masse des Kerns,
die Masse des Kerns, ![]() sein Impuls)
sein Impuls)
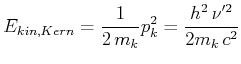 |
(4.59) |
Energieerhaltung:
| (4.60) |
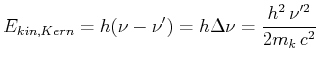
Mit
![]() (Fehler typischerweise kleiner als
(Fehler typischerweise kleiner als ![]()
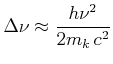 |
(4.61) |
Mössbauers Trick: Atom in Kristall einbetten: dann wird der Impuls von den anderen Atomen im Gitter aufgenommen.
