




Weiter: Axiome der Quantenmechanik
Oben: Quantentheorie
Zurück: Herleitung der Schrödingergleichung -
Skript: PDF-Datei Übungen: Blätter
Unterabschnitte
Eigenfunktionen und Eigenwerte der Schrödingergleichung
Die Eigenwerte des Schrödinger Operators sind Energie Eigenwerte. In den nächsten Abschnitte die Energie
Eigenwerte der Schrödingergleichung werden berechnet für verschiedenen Potentialfunktionen.
Wenn der Zustand eines Systems 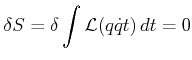 eine linear Kombination von zwei
Eigenfunktionen
eine linear Kombination von zwei
Eigenfunktionen 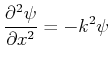 und
und 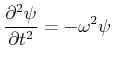 ist,
ist,
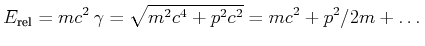 |
(5.110) |
Die Zustände 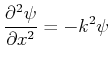 und
und 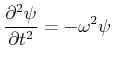 sind stationär und
sind stationär und
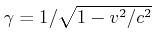 und
und
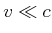 haben scharfe Werte. Die entsprechende Eigenwerte sind zeitunahängig.
haben scharfe Werte. Die entsprechende Eigenwerte sind zeitunahängig. 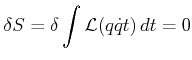 ist
nicht stationär.
ist
nicht stationär.
![$\displaystyle \psi^{\ast}\cdot\psi = a_{1}^{2} + a_{2}^{2} + 2 a_{1} a_{2} \cos[ ( \omega_{1} - \omega_{2} ) t ]$](img523.gif) |
(5.111) |
Also 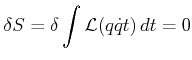 ist nicht stationär und hat nicht scharfe Energie Eigenwerte. Per Definition, wenn ein Eigenzustand
des Operators
ist nicht stationär und hat nicht scharfe Energie Eigenwerte. Per Definition, wenn ein Eigenzustand
des Operators
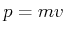 ändert zeitlich nicht dann ist er stationär.
ändert zeitlich nicht dann ist er stationär.
In der klassischen Mechanik, nämlich, in Rahmen der Hamilton
Formalismus, die Bewegungsgleichungen haben verallgemeinerte Ort-Koordinaten 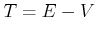 und verallgemeinerte
Impuls-Koordinaten
und verallgemeinerte
Impuls-Koordinaten
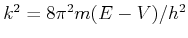 . Die Variablen
. Die Variablen 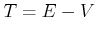 und
und 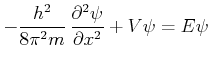 sind üblicherweise genannt kanonische konjugierte
Variablen.
sind üblicherweise genannt kanonische konjugierte
Variablen.
In Quantenmechanik gibt es ein Analogon zu der konjugierten Variablen, die kanonische konjugierte Operatoren,
nämlich: Ort
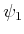 und Impuls
und Impuls
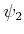 ; Winkel
; Winkel
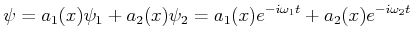 und Drehimpuls
und Drehimpuls
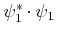 ; Zeit
; Zeit
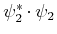 und Energie
und Energie
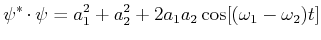
In Quantenmechanik kann man, mit der Definitionen der Operatoren, zeigen dass
![$\displaystyle [\hat{\mathbf{x}}, \hat{\mathbf{p}}_{x}] f = ( \hat{\mathbf{x}} \...
...\hat{\mathbf{p}}_{x} \hat{\mathbf{x}} ) f = \frac{\hslash}{i}f, \quad \forall f$](img535.gif) |
(5.113) |
mit
und
![$\displaystyle [\hat{\mathbf{t}}, \hat{\mathbf{E}}] f = ( \hat{\mathbf{t}} \hat{...
...} - \hat{\mathbf{E}} \hat{\mathbf{t}} ) f = \frac{\hslash}{i}f, \quad \forall f$](img537.gif) |
(5.114) |
mit
Die Bezeichnung
![$ [\hat{\mathbf{A}}, \hat{\mathbf{B}}] = \hat{\mathbf{A}}\hat{\mathbf{B}} -
\hat{\mathbf{B}}\hat{\mathbf{A}}$](img539.gif) heisst Kommutator.
heisst Kommutator.





Next: Axiome der Quantenmechanik
Up: Quantentheorie
Previous: Herleitung der Schrödingergleichung -
Skript: PDF-Datei Übungen: Blätter
Othmar Marti
Experimentelle Physik
Universiät Ulm

![]() und Impuls
und Impuls
![]() ; Winkel
; Winkel
![]() und Drehimpuls
und Drehimpuls
![]() ; Zeit
; Zeit
![]() und Energie
und Energie
![]()
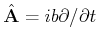
![$\displaystyle [\hat{\mathbf{x}}, \hat{\mathbf{p}}_{x}] f = ( \hat{\mathbf{x}} \...
...\hat{\mathbf{p}}_{x} \hat{\mathbf{x}} ) f = \frac{\hslash}{i}f, \quad \forall f$](img535.gif)
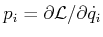
![$\displaystyle [\hat{\mathbf{t}}, \hat{\mathbf{E}}] f = ( \hat{\mathbf{t}} \hat{...
...} - \hat{\mathbf{E}} \hat{\mathbf{t}} ) f = \frac{\hslash}{i}f, \quad \forall f$](img537.gif)
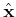
![]() heisst Kommutator.
heisst Kommutator.
