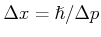




Weiter: Lösung der Schrödingergleichung für
Oben: Quantentheorie
Zurück: Wahrscheinlichkeitsdichte und Wellenfunktionen der
Skript: PDF-Datei Übungen: Blätter
Wenn ein Wellenpaket definiert wird wie eine Gausssche Verteilung von 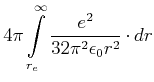 ,
,
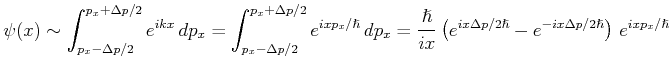 |
(5.122) |
dann die Funktion
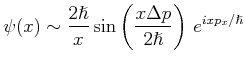 ist eine Gausssche Verteilung von
ist eine Gausssche Verteilung von 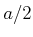 .
.
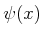 |
(5.123) |
und
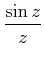 |
(5.124) |
Wenn die Streuung in Ort
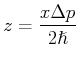 ist, die entsprechende Streuung in Impuls ist
ist, die entsprechende Streuung in Impuls ist
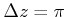 . Dann das Produkt
. Dann das Produkt
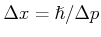 |
(5.125) |
zeigt dass es ist unmöglich gleichzeitig Ort und Impuls mit beliebigen Genauigkeit zu erreichen. Die Relation ist
als Heisenberg
Unschärferelation genannt.
Othmar Marti
Experimentelle Physik
Universiät Ulm
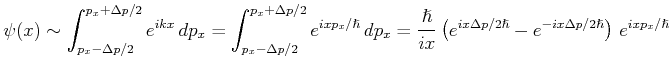

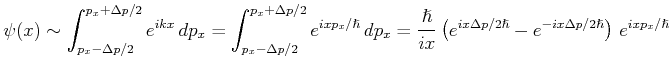
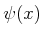
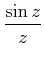
![]() ist, die entsprechende Streuung in Impuls ist
ist, die entsprechende Streuung in Impuls ist
![]() . Dann das Produkt
. Dann das Produkt