




Weiter: Potentialwall und Tunneleffekt
Oben: Quantentheorie
Zurück: Lösung der Schrödingergleichung für
Skript: PDF-Datei Übungen: Blätter
Lösungen der Schrödingergleichung für eine Potentialstufe
Wir können den Ansatz
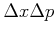 als Lösung der Schrödingergleichung nehmen. Die
Zeitabhängigkeit von
als Lösung der Schrödingergleichung nehmen. Die
Zeitabhängigkeit von 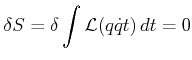 ist harmonisch und, deswegen,
ist harmonisch und, deswegen, 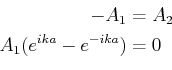 ist eine stationäre Lösung der zeitunabhängigen
Schrödingergleichung.
ist eine stationäre Lösung der zeitunabhängigen
Schrödingergleichung.
Das Problem kann in zwei Fälle geteilt werden: A) - Die Energie der einfallenden Welle 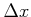 ist grösser als die
Potentielle Energie (
ist grösser als die
Potentielle Energie (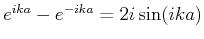 ); B) - Die Energie der einfallenden Welle
); B) - Die Energie der einfallenden Welle 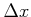 ist kleiner als die Potentielle
Energie (
ist kleiner als die Potentielle
Energie (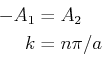 ). Sei
). Sei 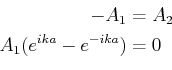 eine einfallende Welle die sich in der positiven Richtung der
eine einfallende Welle die sich in der positiven Richtung der 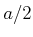 -Achse
ausbreitet. Ihr Impuls ist
-Achse
ausbreitet. Ihr Impuls ist
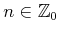 für
für 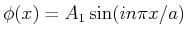 und
und
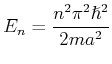 für
für 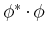 . Die
kinetische Energie ist
. Die
kinetische Energie ist
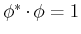 . Also, wir haben
. Also, wir haben
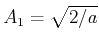 |
(5.133) |
und
 |
(5.134) |
Die Lösungen der Schrödingergleichung müssen zweimal differenzierbar sein, d.h. 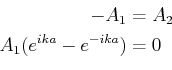 und
und
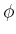 müssen stetig sein für jeder
müssen stetig sein für jeder 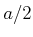 .
. 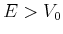 und
und 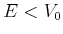 müssen für
müssen für 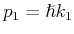 dieselben Werte haben.
Die Eigenfunktion
dieselben Werte haben.
Die Eigenfunktion 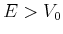 hat für
hat für 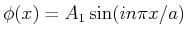 zwei Komponenten: Eine ausbreitende Welle mit Amplitude
zwei Komponenten: Eine ausbreitende Welle mit Amplitude 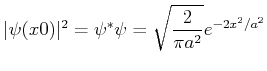 in der
positiven Richtung der
in der
positiven Richtung der 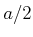 -Achse und eine ausbreitende Welle mit Amplitude
-Achse und eine ausbreitende Welle mit Amplitude 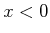 in der negativen Richtung
(reflektierte Welle) der
in der negativen Richtung
(reflektierte Welle) der 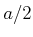 -Achse. Beide mit demselben Impuls
-Achse. Beide mit demselben Impuls
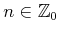 . Für
. Für 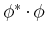 es gibt nur
eine harmonische Welle mit Amplitude
es gibt nur
eine harmonische Welle mit Amplitude 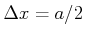 und Impuls
und Impuls
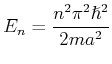 (transmittierte Welle), die sich
in der positiven Richtung der
(transmittierte Welle), die sich
in der positiven Richtung der 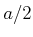 -Achse ausbreitet. Also, wir haben für den ersten Fall,
-Achse ausbreitet. Also, wir haben für den ersten Fall,
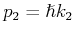 |
(5.135) |
oder
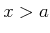 |
(5.136) |
Die Relationen
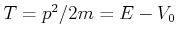 |
(5.137) |
und
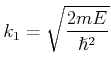 |
(5.138) |
beschreiben die Intensität der Reflexion bzw. der Transmission. Die Energie Erhaltungssatz unterstellt dass
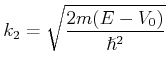 |
(5.139) |
Für den Fall B,
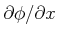 |
(5.140) |
und dann,
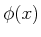 |
(5.141) |





Next: Potentialwall und Tunneleffekt
Up: Quantentheorie
Previous: Lösung der Schrödingergleichung für
Skript: PDF-Datei Übungen: Blätter
Othmar Marti
Experimentelle Physik
Universiät Ulm

![]() ist grösser als die
Potentielle Energie (
ist grösser als die
Potentielle Energie (![]() ); B) - Die Energie der einfallenden Welle
); B) - Die Energie der einfallenden Welle ![]() ist kleiner als die Potentielle
Energie (
ist kleiner als die Potentielle
Energie (![]() ). Sei
). Sei ![]() eine einfallende Welle die sich in der positiven Richtung der
eine einfallende Welle die sich in der positiven Richtung der ![]() -Achse
ausbreitet. Ihr Impuls ist
-Achse
ausbreitet. Ihr Impuls ist
![]() für
für ![]() und
und
![]() für
für ![]() . Die
kinetische Energie ist
. Die
kinetische Energie ist
![]() . Also, wir haben
. Also, wir haben
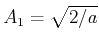

![]() und
und
![]() müssen stetig sein für jeder
müssen stetig sein für jeder ![]() .
. ![]() und
und ![]() müssen für
müssen für ![]() dieselben Werte haben.
Die Eigenfunktion
dieselben Werte haben.
Die Eigenfunktion ![]() hat für
hat für ![]() zwei Komponenten: Eine ausbreitende Welle mit Amplitude
zwei Komponenten: Eine ausbreitende Welle mit Amplitude ![]() in der
positiven Richtung der
in der
positiven Richtung der ![]() -Achse und eine ausbreitende Welle mit Amplitude
-Achse und eine ausbreitende Welle mit Amplitude ![]() in der negativen Richtung
(reflektierte Welle) der
in der negativen Richtung
(reflektierte Welle) der ![]() -Achse. Beide mit demselben Impuls
-Achse. Beide mit demselben Impuls
![]() . Für
. Für ![]() es gibt nur
eine harmonische Welle mit Amplitude
es gibt nur
eine harmonische Welle mit Amplitude ![]() und Impuls
und Impuls
![]() (transmittierte Welle), die sich
in der positiven Richtung der
(transmittierte Welle), die sich
in der positiven Richtung der ![]() -Achse ausbreitet. Also, wir haben für den ersten Fall,
-Achse ausbreitet. Also, wir haben für den ersten Fall,
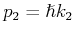
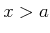
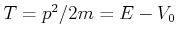
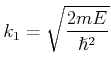
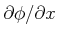
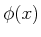
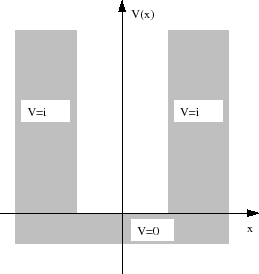
![\includegraphics[height=0.5\textwidth]{FIGURES/PotStufe}](img612.gif)
