




Weiter: Potentialtopf
Oben: Quantentheorie
Zurück: Lösungen der Schrödingergleichung für
Skript: PDF-Datei Übungen: Blätter
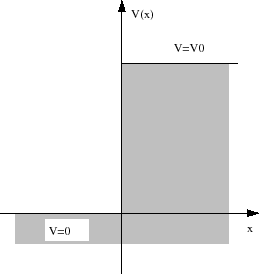
Wenn eine Materiewelle 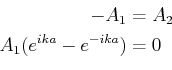 sich in der positiven Richtung der
sich in der positiven Richtung der  -Achse ausbreitet, für
-Achse ausbreitet, für  und
und 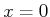 (Abbild. 5.4).
(Abbild. 5.4).
Wenn Die Energie des Teilchens 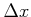 kleiner ist als das Potential des Walls
kleiner ist als das Potential des Walls 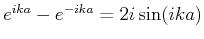 dann wir setzen die
allgemeine Ansätze,
dann wir setzen die
allgemeine Ansätze,
wobei,
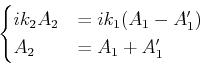 . Für
. Für 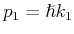 und
und 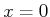 setzen wir die Randbedingungen,
setzen wir die Randbedingungen,
und
Wir setzen
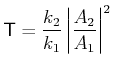 weil keine Reflexion erwartet ist für
weil keine Reflexion erwartet ist für 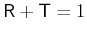 . Wir haben dann,
. Wir haben dann,
bzw.
Wir erreichen die folgende Identität:
Also wir können jetzt die Transmission und Reflexion Koeffizienten
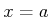 , bzw.
, bzw.
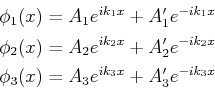 wie folgend,
wie folgend,
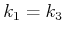 |
(5.148) |
und
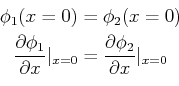 |
(5.149) |
wobei
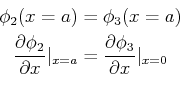 ,
,
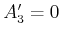 und
und
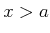 . Die Transmission ist eine oszillierende Funktion der Breite des Walls
. Die Transmission ist eine oszillierende Funktion der Breite des Walls  . Wir
können auch schreiben,
. Wir
können auch schreiben,
![$\displaystyle \mathsf{T} = \frac{4E(E - V_{0})}{4 E(E - V_{0}) + V_{0}^{2}\sin^{2}\left[\sqrt{2 m(E - V_{0})} a / \hslash \right]}$](img630.gif) |
(5.150) |
Für den Fall 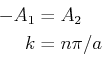 , wir schreiben
, wir schreiben 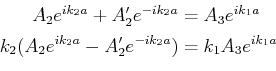 wie folgend,
wie folgend,
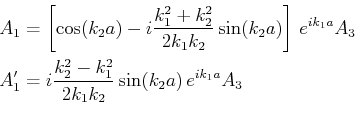 |
(5.151) |
mit
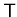 und
und
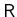 . Im diesen Fall die Transmission
. Im diesen Fall die Transmission
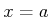 wird
wird
![$\displaystyle \mathsf{T} = \frac{4E(E-V_{0})}{4 E(V_{0} - E) + V_{0}^{2}\sin^{2}\left[\sqrt{2 m(V_{0} - E)} a / \hslash\right]}$](img635.gif) |
(5.152) |
mit
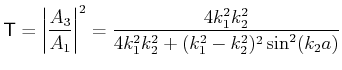 . Für
. Für
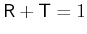 ,
,
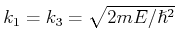 |
(5.153) |
Wenn ein Elektron mit Energie 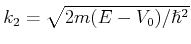 sich bewegt in der Richtung einem Potentialwall mit
Breite
sich bewegt in der Richtung einem Potentialwall mit
Breite 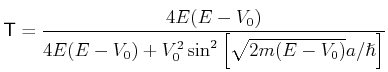 angstrom und Höhe
angstrom und Höhe 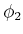 , dann die Transmission ist
, dann die Transmission ist
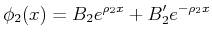 . Für dieselben Bedingungen ein Proton (
. Für dieselben Bedingungen ein Proton (
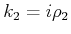 )
)
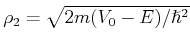 .
Das heisst, das Tunneleffekt ist für ein Elektron sehr wahrscheinlich, aber für den Proton fast unmöglich.
.
Das heisst, das Tunneleffekt ist für ein Elektron sehr wahrscheinlich, aber für den Proton fast unmöglich.
Das Rastertunnelmikroskop (STM) beruht auf dem Tunneleffekt. Die Elektronen können eine enge Potentialbarriere
durchqueren. Der Tunnelstrom verringert sich mit der Breite der Barriere exponentiell.

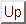




Next: Potentialtopf
Up: Quantentheorie
Previous: Lösungen der Schrödingergleichung für
Skript: PDF-Datei Übungen: Blätter
Othmar Marti
Experimentelle Physik
Universiät Ulm

![]() kleiner ist als das Potential des Walls
kleiner ist als das Potential des Walls ![]() dann wir setzen die
allgemeine Ansätze,
dann wir setzen die
allgemeine Ansätze,
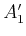
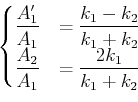
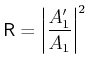
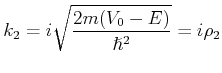
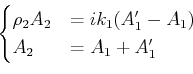
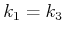
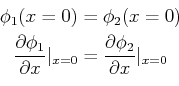
![$\displaystyle \mathsf{T} = \frac{4E(E - V_{0})}{4 E(E - V_{0}) + V_{0}^{2}\sin^{2}\left[\sqrt{2 m(E - V_{0})} a / \hslash \right]}$](img630.gif)
![]() , wir schreiben
, wir schreiben ![]() wie folgend,
wie folgend,
![$\displaystyle \mathsf{T} = \frac{4E(E-V_{0})}{4 E(V_{0} - E) + V_{0}^{2}\sin^{2}\left[\sqrt{2 m(V_{0} - E)} a / \hslash\right]}$](img635.gif)
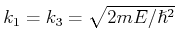
![]() sich bewegt in der Richtung einem Potentialwall mit
Breite
sich bewegt in der Richtung einem Potentialwall mit
Breite ![]() angstrom und Höhe
angstrom und Höhe ![]() , dann die Transmission ist
, dann die Transmission ist
![]() . Für dieselben Bedingungen ein Proton (
. Für dieselben Bedingungen ein Proton (
![]() )
)
![]() .
Das heisst, das Tunneleffekt ist für ein Elektron sehr wahrscheinlich, aber für den Proton fast unmöglich.
.
Das heisst, das Tunneleffekt ist für ein Elektron sehr wahrscheinlich, aber für den Proton fast unmöglich.
![\includegraphics[height=0.5\textwidth]{FIGURES/PotWall}](img645.gif)
