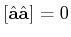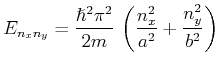




Weiter: Atome und ihr Aufbau
Oben: Quantentheorie
Zurück: Potentialtopf
Skript: PDF-Datei Übungen: Blätter
Unterabschnitte
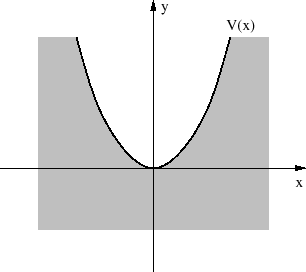
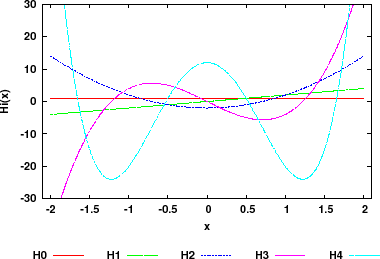
Wenn die potentielle Energie 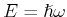 eine quadratische Abhängigkeit von
eine quadratische Abhängigkeit von 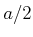 hat, dann ist die Bewegung des Teilchens
beschränkt wie in dem Fall eines klassischen harmonischen Oszillator. Der Operator
hat, dann ist die Bewegung des Teilchens
beschränkt wie in dem Fall eines klassischen harmonischen Oszillator. Der Operator
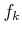 hat die
Form,
hat die
Form,
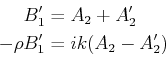 |
(5.162) |
mit
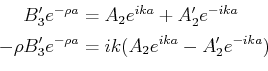 |
(5.163) |
Die Lösungen der Schrödinger Gleichung sind stationär und haben die Form,
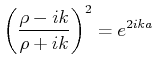 |
(5.164) |
Damit können wir die zeitunabhängige Schrödinger Gleichung verwenden,
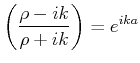 |
(5.165) |
Potentialfunktion eines harmonischen Oszillators.
|
Wir können drei Parameter definieren und die Variable 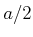 ersetzen
ersetzen
Die Gleichung 5.73 wird dann geschrieben wie es folgt,
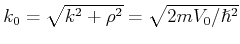 |
(5.167) |
Um die Eigenfunktion 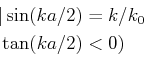 und die Eigenwerte
und die Eigenwerte
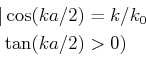 bzw.
bzw. 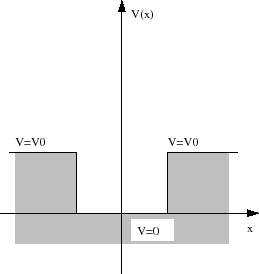 zu finden, können wir die folgenden
Operatoren verwenden,
zu finden, können wir die folgenden
Operatoren verwenden,
Die Operatoren
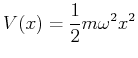 und
und
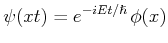 sind nicht hermitisch (also, selbstadjungiert)
aber sie sind adjungiert zueinander. Man kann dann schreiben,
sind nicht hermitisch (also, selbstadjungiert)
aber sie sind adjungiert zueinander. Man kann dann schreiben,
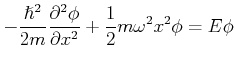 |
(5.169) |
und
 |
(5.170) |
Die Hamiltonsche Funktion wird dann definiert als
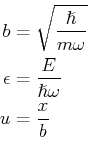 |
(5.171) |
Der Kommutator Operator ergibt
![$\displaystyle [\hat{\mathbf{a}}, \hat{\mathbf{a}}^{\dagger}] = \hat{\mathbf{a}}\hat{\mathbf{a}}^{\dagger} - \hat{\mathbf{a}}^{\dagger} \hat{\mathbf{a}} = 1$](img677.gif) |
(5.172) |
Gleichzeitig, wenn wir die Eigenschaften des Kommutators anwenden haben wir,
![$\displaystyle [ \hat{\mathbf{a}}, \hat{\mathbf{a}} ] = 0$](img678.gif) |
(5.173) |
und
![$\displaystyle [ \hat{\mathbf{a}}^{\dagger}, \hat{\mathbf{a}}^{\dagger} ] = 0$](img679.gif) |
(5.174) |
Wenn wir die Eigenschaften der linearen Operatoren verwenden können wir weitere Gleichungen ableiten, z.B.
und
Wegen der Eigenschaften oben dargestellt, werden die Operatoren
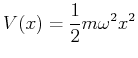 und
und
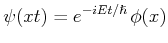 als Erzeugungsoperator oder Aufstiegsoperator bzw. Vernichtungsoperator oder Abstiegsoperator.
als Erzeugungsoperator oder Aufstiegsoperator bzw. Vernichtungsoperator oder Abstiegsoperator.
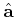 |
(5.178) |
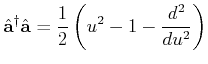 |
(5.179) |
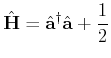 |
(5.181) |
Die Energieeigenwerte eines zweidimensionalen
Potentialtopfs sind ähnlich quantisiert wie in dem Fall eines eindimensionalen Topfs. Wenn der Topf die Dimensionen  und
und 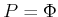 hat (siehe Abbildung 5.8), dann sind die Energieeigenwerte in diesem Fall
hat (siehe Abbildung 5.8), dann sind die Energieeigenwerte in diesem Fall
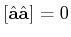 |
(5.182) |
mit 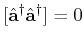 ,
,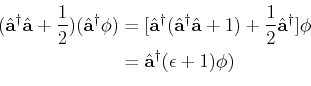 Ganzzahlen
Ganzzahlen 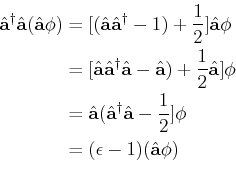 . Die Eigenfunktionen lauten
. Die Eigenfunktionen lauten
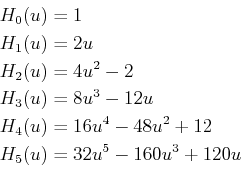 |
(5.183) |
Wenn  oder
oder 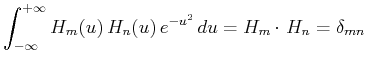 (mit
(mit  Ganzzahl) dann verschiedene Eigenfunktionen können denselben Energie
Eigenwerte haben, d.h. die Eigenwerte sind entartet. Z.B., wenn
Ganzzahl) dann verschiedene Eigenfunktionen können denselben Energie
Eigenwerte haben, d.h. die Eigenwerte sind entartet. Z.B., wenn 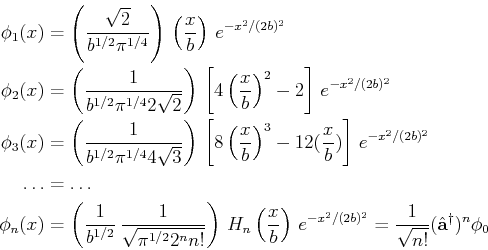 , zu den Paare
, zu den Paare
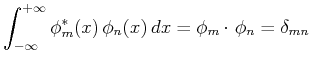 und
und
 entspricht dieselbe Energie:
entspricht dieselbe Energie:
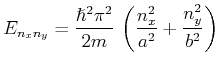 |
(5.184) |
2D unendlicher Potentialkasten.
|
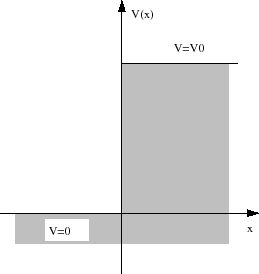
Der Fall eines Teilchens in einem endlichen Potentialtopf ist etwas
komplizierter als der Fall des unendlichen. Die Wellenfunktion verschwindet nicht am Rand des Topfes. Die
Übergänge erzeugen jedoch Reflexionen. Wenn eine Welle 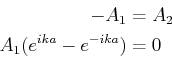 sich in der positiven Richtung der
sich in der positiven Richtung der 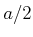 -Achse
ausbreitet, für
-Achse
ausbreitet, für 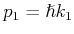 und
und 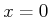
Wenn Die Energie des Teilchens 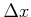 kleiner ist als das Potential des Walls
kleiner ist als das Potential des Walls 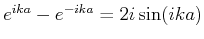 dann wir setzen die
allgemeine Ansätze,
dann wir setzen die
allgemeine Ansätze,
wobei,
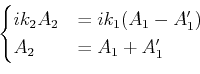 . Für
. Für 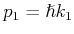 und
und 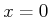 setzen wir die Randbedingungen,
setzen wir die Randbedingungen,
und
Wir setzen
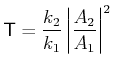 weil keine Reflexion erwartet ist für
weil keine Reflexion erwartet ist für 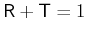 . Wir haben dann,
. Wir haben dann,
bzw.
Wir erreichen die folgende Identität:
Also wir können jetzt die Transmission und Reflexion Koeffizienten
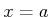 , bzw.
, bzw.
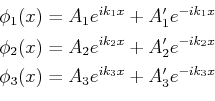 wie folgend,
wie folgend,
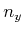 |
(5.191) |
und
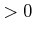 |
(5.192) |
wobei
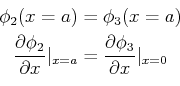 ,
,
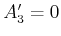 und
und
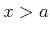 . Die Transmission ist eine oszillierende Funktion der Breite des Walls
. Die Transmission ist eine oszillierende Funktion der Breite des Walls  . Wir
können auch schreiben,
. Wir
können auch schreiben,
![$\displaystyle \mathsf{T} = \frac{4E(E - V_{0})}{4 E(E - V_{0}) + V_{0}^{2}\sin^{2}\left[\sqrt{2 m(E - V_{0})} a / \hslash \right]}$](img630.gif) |
(5.193) |
Für den Fall  , wir schreiben
, wir schreiben  wie folgend,
wie folgend,
 |
(5.194) |
mit
 und
und
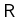 . Im diesen Fall die Transmission
. Im diesen Fall die Transmission
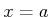 wird
wird
![$\displaystyle \mathsf{T} = \frac{4E(E-V_{0})}{4 E(V_{0} - E) + V_{0}^{2}\sin^{2}\left[\sqrt{2 m(V_{0} - E)} a / \hslash\right]}$](img635.gif) |
(5.195) |
mit
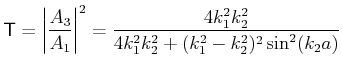 . Für
. Für
 ,
,
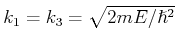 |
(5.196) |
Wenn ein Elektron mit Energie 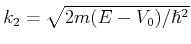 sich bewegt in der Richtung einem Potentialwall mit
Breite
sich bewegt in der Richtung einem Potentialwall mit
Breite 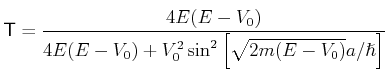 angstrom und Höhe
angstrom und Höhe 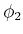 , dann die Transmission ist
, dann die Transmission ist
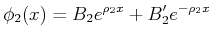 . Für dieselben Bedingungen ein Proton (
. Für dieselben Bedingungen ein Proton (
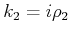 )
)
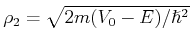 .
Das heisst, das Tunneleffekt ist für ein Elektron sehr wahrscheinlich, aber für den Proton fast unmöglich.
.
Das heisst, das Tunneleffekt ist für ein Elektron sehr wahrscheinlich, aber für den Proton fast unmöglich.
Das Rastertunnelmikroskop (STM) beruht auf dem Tunneleffekt. Die Elektronen können eine enge Potentialbarriere
durchqueren. Der Tunnelstrom verringert sich mit der Breite der Barriere exponentiell.
Die Energie Eigenwerte eines zweidimensionalen Potentialtopf sind ähnlich
quantisiert wie in dem Fall eines eindimensionalen Topfs. Wenn der Topf Dimensionen  und
und 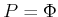 hat, die Energie
Eigenwerte sind in diesem Fall
hat, die Energie
Eigenwerte sind in diesem Fall
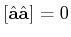 |
(5.197) |
mit 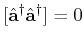 ,
,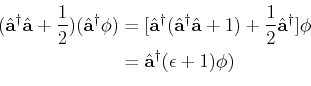 Ganzzahlen
Ganzzahlen 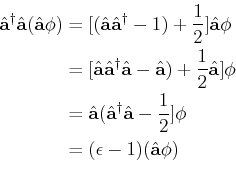 . Die Eigenfunktionen lauten
. Die Eigenfunktionen lauten
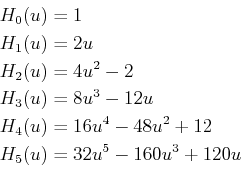 |
(5.198) |
Wenn  oder
oder 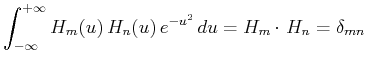 (mit
(mit  Ganzzahl) dann verschiedene Eigenfunktionen können denselben Energie
Eigenwerte haben, d.h. die Eigenwerte sind entartet. Z.B., wenn
Ganzzahl) dann verschiedene Eigenfunktionen können denselben Energie
Eigenwerte haben, d.h. die Eigenwerte sind entartet. Z.B., wenn 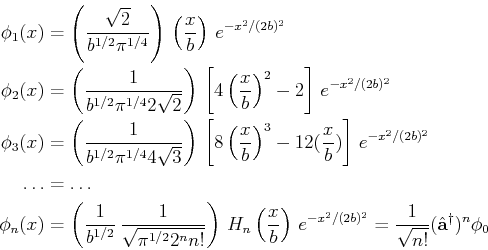 zu den Paare
zu den Paare
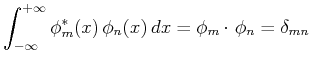 und
und
 entspricht dieselbe Energie:
entspricht dieselbe Energie:
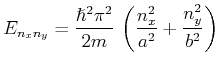 |
(5.199) |





Next: Atome und ihr Aufbau
Up: Quantentheorie
Previous: Potentialtopf
Skript: PDF-Datei Übungen: Blätter
Othmar Marti
Experimentelle Physik
Universiät Ulm
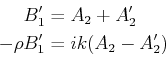

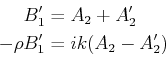
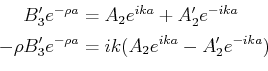
![\includegraphics[height=0.5\textwidth]{FIGURES/HarmOszil2}](img665.gif)
![]() ersetzen
ersetzen
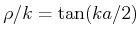
![]() und die Eigenwerte
und die Eigenwerte
![]() bzw.
bzw. ![]() zu finden, können wir die folgenden
Operatoren verwenden,
zu finden, können wir die folgenden
Operatoren verwenden,
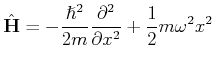
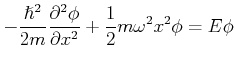

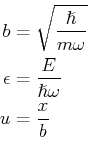
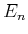
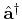
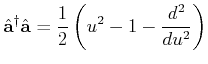
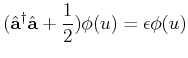
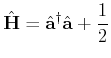
![\includegraphics[height=0.5\textwidth]{FIGURES/HermitePolynome}](img687.gif)
![]() und
und ![]() hat (siehe Abbildung 5.8), dann sind die Energieeigenwerte in diesem Fall
hat (siehe Abbildung 5.8), dann sind die Energieeigenwerte in diesem Fall
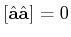
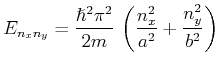
![\includegraphics[height=0.5\textwidth]{FIGURES/2DUnendPotKasten}](img699.gif)
![]() sich in der positiven Richtung der
sich in der positiven Richtung der ![]() -Achse
ausbreitet, für
-Achse
ausbreitet, für ![]() und
und ![]()
![]() kleiner ist als das Potential des Walls
kleiner ist als das Potential des Walls ![]() dann wir setzen die
allgemeine Ansätze,
dann wir setzen die
allgemeine Ansätze,
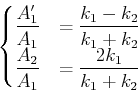
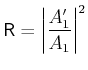
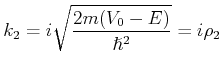
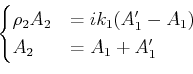
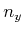
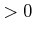
![$\displaystyle \mathsf{T} = \frac{4E(E - V_{0})}{4 E(E - V_{0}) + V_{0}^{2}\sin^{2}\left[\sqrt{2 m(E - V_{0})} a / \hslash \right]}$](img630.gif)
![]() , wir schreiben
, wir schreiben ![]() wie folgend,
wie folgend,
![$\displaystyle \mathsf{T} = \frac{4E(E-V_{0})}{4 E(V_{0} - E) + V_{0}^{2}\sin^{2}\left[\sqrt{2 m(V_{0} - E)} a / \hslash\right]}$](img635.gif)
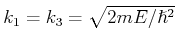
![]() sich bewegt in der Richtung einem Potentialwall mit
Breite
sich bewegt in der Richtung einem Potentialwall mit
Breite ![]() angstrom und Höhe
angstrom und Höhe ![]() , dann die Transmission ist
, dann die Transmission ist
![]() . Für dieselben Bedingungen ein Proton (
. Für dieselben Bedingungen ein Proton (
![]() )
)
![]() .
Das heisst, das Tunneleffekt ist für ein Elektron sehr wahrscheinlich, aber für den Proton fast unmöglich.
.
Das heisst, das Tunneleffekt ist für ein Elektron sehr wahrscheinlich, aber für den Proton fast unmöglich.