|
|

|
|
|
|
Elektron hat Spin
![]() Drehimpulsvektor
Drehimpulsvektor
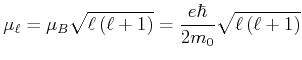 analog zu analog zu |
||
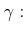 |
![\includegraphics[width=0.4\textwidth]{elektron-001}](img1315.gif)
Elektronenspin
|
gyromagnetisches Verhältnis
![]()
Bahndrehimpuls
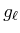 |
||
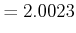 |
|
|
![]() bilden Gesamtdrehimpuls
bilden Gesamtdrehimpuls ![]()
mit
![]() -Elektron
-Elektron ![]() ,
,
![]()
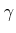 |
||
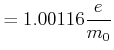 |
für ![]() wird
wird ![]()
Richtungsquantisierung
![\includegraphics[width=0.5\textwidth]{elektron-002}](img1336.gif)
Spin-Bahn-Kopplung
|
zu ![]() gehört
gehört
![]()
Auswahlregel:
![]() Übergang
Übergang
![]() verboten
verboten
![\includegraphics[width=0.8\textwidth]{elektron-003}](img1340.gif)
Spin-Bahnkopplung nach Bohr
|
Biot-Savart
Magnetfeld von ![]()
![$\displaystyle =+\frac{Ze\mu_{0}}{4\pi r^{3}}\left[ \vec{\nu} \times\left( -\vec{r}\right) \right]$](img1343.gif) |
||
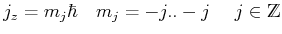 |
da
![]() ist
ist
![]()
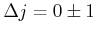
Rücktrafo: Faktor
![]() Thomasfaktor aus rel. Betrachtung
Thomasfaktor aus rel. Betrachtung
Spin präzediert um
![]()
![\includegraphics[width=0.4\textwidth]{elektron-004}](img1349.gif)
![\includegraphics[width=0.4\textwidth]{elektron-005}](img1350.gif)
Spinpräzession. Links Skizze, rechts Vektoraddition
|
![]() potentielle Energie
potentielle Energie
mit ![]()
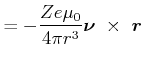
(mit Thomaskorrektur)
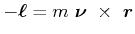 |
||
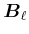 |
||
![$\displaystyle =\frac{a}{2\hbar^{2}}\left[ \left\vert j\right\vert ^{2}-\left\vert \ell\right\vert ^{2}-\left\vert s\right\vert ^{2}\right]$](img1358.gif) |
||
![$\displaystyle =\frac{a}{2}\left[ j\left( j+1\right) -\ell\left( \ell+1\right) -s\left( s+1\right) \right]$](img1359.gif) |
![]() in
in ![]() ist
ist ![]() , der Radius der
, der Radius der ![]() -ten Bohrschen Bahn.
-ten Bohrschen Bahn.
Dann ist
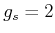
und
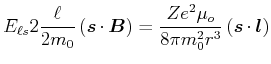
und nach Mitteilung
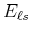
![\includegraphics[width=0.4\textwidth]{elektron-006}](img1364.gif)
p-Aufspaltung
|
![\includegraphics[width=0.3\textwidth]{esr-001}](img1365.gif)
Elektronenspinresonanz
|
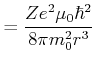
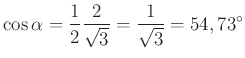
Energieunterschied ![]()
![\includegraphics[width=0.3\textwidth]{esr-002}](img1372.gif)
Situation von oben gesehen
|
Übergänge treten auf, wenn
oder
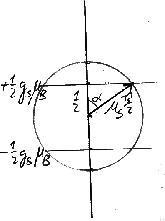
Präzessionsfrequenz:
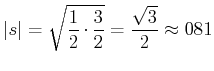
![\includegraphics[width=0.7\textwidth]{esr-003}](img1376.gif)
Elektronen-Spin-Resonanz: Aufbau
|
|
|
![\includegraphics[width=0.5\textwidth]{zeemann-001}](img1377.gif)
Zeemann-Effekt klassisch
|
Lineare Schwingung schräg zum ![]() -Feld entspricht
-Feld entspricht
![]() -Feld beeinflusst 1) nicht
-Feld beeinflusst 1) nicht
2), 3) werden beschleunigt oder gebremst (Larmor-Frequenz)

Kräftegleichgewicht im Atom
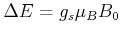
wir haben noch die Lorentz-Kraft
![\begin{displaymath}\begin{array}[c]{crcc}(a) & m_{0} \ddot{x}+m_{0}\omega_{0}^{...
...
(c) & m_{0} \ddot{z}+m_{0}\omega_{0}^{2}z & = & 0
\end{array}\end{displaymath}](img1381.gif)
aus (c) folgt, dass
![]() unverändert bleibt.
unverändert bleibt.
Wir setzen ![]() und
und ![]()
oder
![]()
![\begin{displaymath}\begin{array}[c]{ccccc}(a) & \frac{m_{0}}{2}\left( \ddot{u}+\...
...v}\right) B_{0} & = & 0 & \left\vert \cdot2i\right.
\end{array}\end{displaymath}](img1386.gif)
![\begin{displaymath}\begin{array}[c]{ccccc}(a) & m_{0}i\left( \ddot{u}+\ddot{v}\r...
...t) +ie\left(
\dot{u}+\dot{v}\right) B_{0} & = & 0 &
\end{array}\end{displaymath}](img1387.gif)
![\begin{displaymath}\begin{array}[c]{ccccc}(a)+(b) & 2m_{0}\ddot{u}+2m_{0}\omega_...
...0}\omega_{0}^{2}v-2ie \dot{v}\cdot B_{o} & = & 0 &
\end{array}\end{displaymath}](img1389.gif)
Lösungen:
![$\displaystyle =u_{0}\exp\left[ i\left( \omega_{0}-\frac{eB_{0}}{2m}\right) t\right]$](img1390.gif) |
||
![$\displaystyle =v_{0}\exp\left[ i\left( \omega_{0}+\frac{eB_{0}}{2m}\right) t\right]$](img1392.gif) |
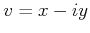 |
||
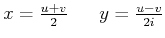 |
||
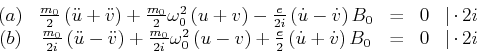 |
||
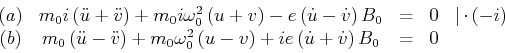 |
das heisst, wenn
![]() ist, wird die Gleichung gelöst.
ist, wird die Gleichung gelöst.
Die Frequenz ändert sich wie
mit
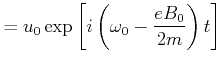
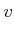
![]() d.h. der klassische Zeemanneffekt bewirkt eine konstante Frequenzverschiebung.
d.h. der klassische Zeemanneffekt bewirkt eine konstante Frequenzverschiebung.
![]() Zeemann-Triplett
Zeemann-Triplett
![]()
normaler Zeemann-Effekt wenn ![]() und
und ![]() nicht koppeln.
nicht koppeln.
anomaler Zeemanneffekt ![]() und
und ![]() koppeln
koppeln
![]() -Faktoren der Terme sind unterschiedlich
-Faktoren der Terme sind unterschiedlich
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Zeemann-Effekt, Quantenmechanik
Hamiltonoperator im Magnetfeld
Vermutung
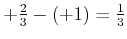 |
||
Rechnung mit kanonischen Impulsen
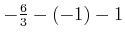 |
||
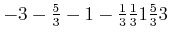 |
||
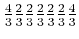 |
![]() vernachlässige
vernachlässige
![]() Diamagnetismus
Diamagnetismus
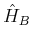
mit
Da die Eigenfunktion für
![]() bekannt sind
bekannt sind
Der Messwert einer Grösse ist durch

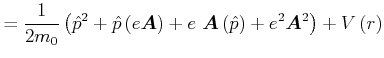 |
||
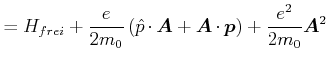 |
mit
![$ \left[ \hat{H}_{frei},\hat{V}_{Zee}\right] =0$](img1436.gif)
Tripletts, aber Dipol-Auswahlregeln erlauben nur
Ca, Yb zeigen normalen Zeemann-Effekt, alle anderen Atome zeigen den anomalen Zeemann-Effekt.
Paschen-Back-Effekt
hohes Magnetfeld
![]() und
und ![]() koppeln nicht mehr
koppeln nicht mehr
