
Weiter: Erhaltungssätze und Erhaltungsgrössen Oben: Mechanik in drei Dimensionen Zurück: Mechanik in drei Dimensionen Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Die Lage eines Massenpunktes wird durch seinen Ortsvektor angegeben.
![$\displaystyle \left( \begin{array}[c]{r} x y z \end{array} \right)$](img516.gif) |
![$\displaystyle \left( \begin{array}[c]{r} r \varphi \theta \end{array} \right)$](img518.gif) |
![$\displaystyle \left( \begin{array}[c]{r} \rho \varphi z \end{array} \right)$](img519.gif) |
||||||
![\includegraphics[height=0.15\textheight]{mechanik-001}](img523.gif)
![\includegraphics[height=0.15\textheight]{mechanik-002}](img524.gif)
![\includegraphics[height=0.15\textheight]{mechanik-003}](img525.gif)
Definition der Koordinatensysteme. Links: kartesisches System. Mitte:
Zylinderkoordinaten. Rechts: Kugelkoordinaten
|
Ein Massenpunkt bewege sich am Hang einer Bahnlinie
![\includegraphics[width=0.4\textwidth]{mechanik-008}](img526.gif)
Bewegung eines Massenpunktes.
|
Die Zeit ![]() ist ein Parameter.
ist ein Parameter.
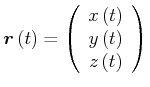 |
(4.78) |
|
Verschiebung
![]()
Beispiel:
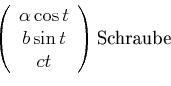 |
|||
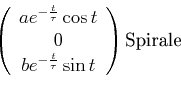 |
|||
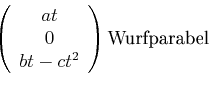 |
|||
 |
Abstand von Ursprung
![]()
Definition:
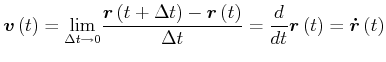 |
(4.79) |
In kartesischen Koordinaten mit
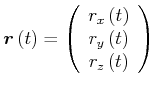 |
ist
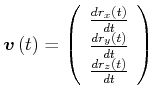 |
(4.80) |
Beispiel: Schraube
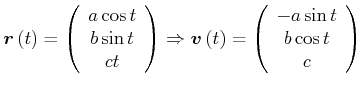 |
Spirale
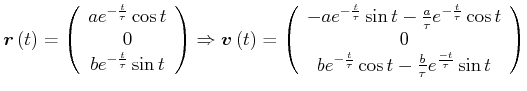 |
Wurfparabel
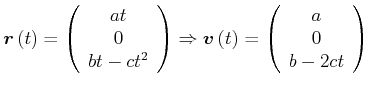 |
Der Betrag der Geschwindigkeit ist
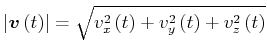 |
|||
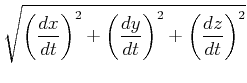 |
![\includegraphics[width=0.7\textwidth]{mechanik-009}](img546.gif)
|
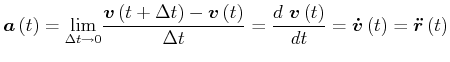 |
(4.81) |
Wichtig:
![]() steht beliebig zur Bahn
steht beliebig zur Bahn
Beispiel: Schraube
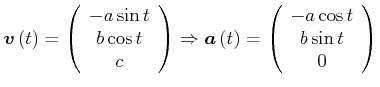 |
also ist
![]() senkrecht auf
senkrecht auf
![]() , d.h. senkrecht auf der Bahntangente
, d.h. senkrecht auf der Bahntangente
Wurfparabel:
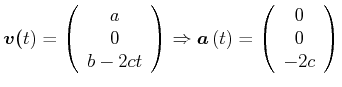 |
Betrag
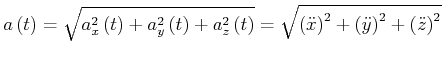 |
Zur Erinnerung ist hier nochmals die Definition der Kugelkoordinaten:
![\includegraphics[height=0.25\textheight]{mechanik-003}](img553.gif)
Definition der Kugelkoordinaten
|
Ort
| (4.82) | |||
| (4.83) | |||
| (4.84) |
mit
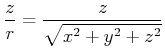 |
|||
Die Geschwindigkeit in Kugelkoordinaten ist
| (4.85) | |||
| (4.86) | |||
| (4.87) | |||
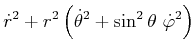 |
(4.88) |
Schliesslich ist die Beschleunigung in Kugelkoordinaten
| (4.89) | |||
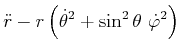 |
|||
| (4.90) | |||
| (4.91) | |||
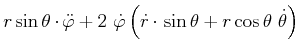 |
|||
| (4.92) | |||
Eine Ableitung der Gleichungen befindet sich im Anhang G.
Wir betrachten eine Bewegung in der ![]() -Ebene
-Ebene
![\includegraphics[width=0.4\textwidth]{mechanik-010}](img589.gif)
Bewegung in einer Ebene
|
Definitionen
Der Ortsvektor ist:
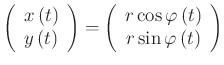 |
(4.93) | ||
| (4.94) |
Daraus erhalten wir unter der Annahme, dass ![]() konstant sei, die Winkelgeschwindigkeit:
konstant sei, die Winkelgeschwindigkeit:
Definition:
![]()
(Alle Rechnungen müssen im Bogenmass durchgeführt werden.)
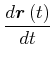 |
(4.95) | ||
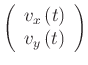 |
(4.96) | ||
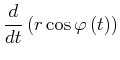 |
(4.97) | ||
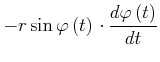 |
(4.98) | ||
| (4.99) | |||
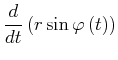 |
(4.100) | ||
| (4.101) |
also
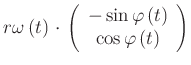 |
(4.102) | ||
| (4.103) |
Die Radialkomponente der Geschwindigkeit ist
| (4.104) |
die Tangentialkomponente ist
| (4.105) |
Für die Beschleunigung erhalten wir
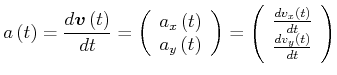 |
(4.106) |
mit
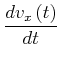 |
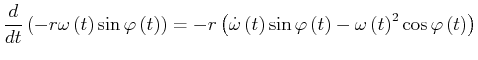 |
(4.107) | |
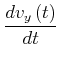 |
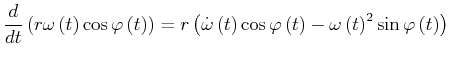 |
(4.108) |
also ist
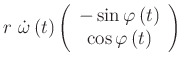 |
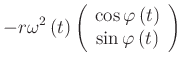 |
(4.109) | |
| Tangentialkomponente | Radialkomponente |
(4.110) |
also ist
![]() die ins Zentrum gerichtete Zentripetalbeschleunigung
die ins Zentrum gerichtete Zentripetalbeschleunigung
und
![]() die den Geschwindigkeitsbetrag erhöhende
Tangentialbeschleunigung
die den Geschwindigkeitsbetrag erhöhende
Tangentialbeschleunigung
mit dem Betrag der Beschleunigung
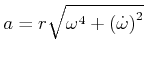
Die obige Rechnung kann sehr viel bequemer mit komplexen Zahlen durchgeführt werden.
![\includegraphics[width=0.9\textwidth]{mechanik-011}](img619.gif)
Kartesische und komplexe Ebene
|
Es gelten die Beziehungen
| (4.111) | ||
| (4.112) | ||
| (4.113) |
Es gilt:
| (4.114) | |||
| (4.115) | |||
| (4.116) |
daher ist auch
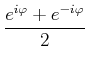 |
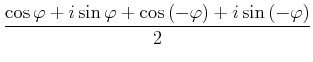 |
(4.117) | |
| (4.118) | |||
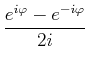 |
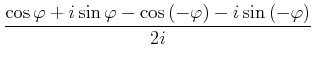 |
(4.119) | |
| (4.120) |
Eine Kreisbahn wird mit komplexen Zahlen durch
| (4.121) | |||
| (4.122) |
beschrieben. Wir erhalten die konjugiert komplexe Grösse
| (4.123) |
| (4.124) | ||
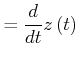 |
||
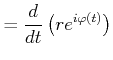 |
||
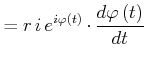 |
||
wobei
![]() die Winkelgeschwindigkeit ist.
die Winkelgeschwindigkeit ist.
| (4.125) | |||
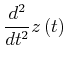 |
(4.126) | ||
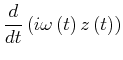 |
(4.127) | ||
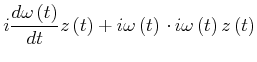 |
(4.128) | ||
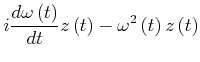 |
(4.129) |
Der erste Summand ist wieder die Tangentialbeschleunigung, während der zweite die Zentripetalbeschleunigung beschreibt
![\includegraphics[width=0.7\textwidth]{mechanik-012}](img652.gif)
Definition des Tangenteneinheitsvektors
|
Um die Kinematik in drei Dimensionen berechnen zu können, müssen wir die Differentialgeometrie von Bahnen verstehen. Wir definieren den Ortsvektor als
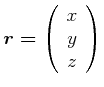 |
(4.130) |
Für eine infinitesimale Strecke ist der zurückgelegte Weg
| (4.131) |
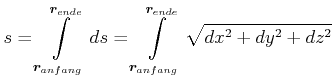 |
(4.132) |
Die Bahn (Trajektorie) des Massenpunktes wird durch die Streckenlänge ![]() auf der Bahn bestimmt. Diese Definition
ist ähnlich wie die im täglichen Leben übliche, ausser dass dort in der Regel Richtungen nicht berücksichtigt
werden.
auf der Bahn bestimmt. Diese Definition
ist ähnlich wie die im täglichen Leben übliche, ausser dass dort in der Regel Richtungen nicht berücksichtigt
werden.
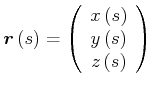 |
(4.133) |
Der Tangentenvektor ist
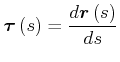 |
(4.134) |
Beweis:
Die Tangentialrichtung ist durch
![]() gegeben. Also ist
gegeben. Also ist
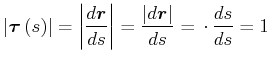 |
(4.135) |
Den Einheitsvektor senkrecht auf die Bahn (auch Bahnnormale genannt)
![]() und den
Krümmungsradius
und den
Krümmungsradius
![]() bekommt man aus
bekommt man aus
![]() durch Ableitung
durch Ableitung
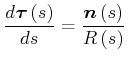 mit mit |
(4.136) |
Beweis:
| (4.137) | |||
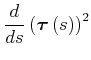 |
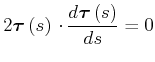 |
(4.138) |
also ist
![]() senkrecht zur Ableitung bezogen auf die Streckenlänge der
Bahn
senkrecht zur Ableitung bezogen auf die Streckenlänge der
Bahn
![]() .
.
![\includegraphics[width=0.5\textwidth]{mechanik-013}](img673.gif)
Berechnung des Krümmungsradius
|
Betrachtet man den an die Bahn geschmiegten Krümmungsradius
![]() , so kann aus der Wegstrecke eine
Winkeländerung berechnet werden.
, so kann aus der Wegstrecke eine
Winkeländerung berechnet werden.
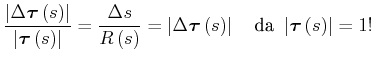 |
(4.139) |
also ist
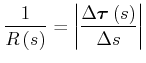 |
(4.140) |
und
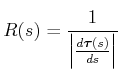 |
(4.141) |
Wir zerlegen die Beschleunigung in ihre Tangentialkomponente
![]() und die Radialkomponente
und die Radialkomponente
![]() .
.
![\includegraphics[width=0.7\textwidth]{mechanik-014}](img678.gif)
Tangentialbeschleunigung
|
Die Änderung des Ortsvektor
![]() erhalten wir aus der Differentialgeometrie. Wir nennen
erhalten wir aus der Differentialgeometrie. Wir nennen
![]() den Fahrplan. Also ist der Ortsvektor auch eine Funktion der Zeit
den Fahrplan. Also ist der Ortsvektor auch eine Funktion der Zeit
![]()
| (4.142) | |||
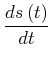 |
(4.143) |
definiert.
Beweis:
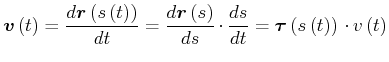 |
(4.144) |
Bemerkung : Dies ist die Definition der Geschwindigkeit, die wir üblicherweise geben würden, aber ohne
auf die Richtung
![]() zu achten.
zu achten.
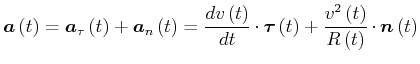 |
(4.145) |
![]() heisst die Tangentialbeschleunigung
heisst die Tangentialbeschleunigung
![]() heisst die Zentripetalbeschleunigung
heisst die Zentripetalbeschleunigung
Beweis:
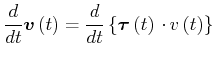 |
(4.146) | ||
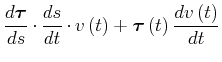 |
(4.147) | ||
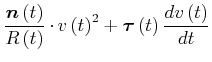 |
(4.148) |
Bemerkung: Wenn wir eine gekrümmte Bahn haben, also
![]() (Kurve), gibt es die
Zentripetalbeschleunigung, sogar wenn
(Kurve), gibt es die
Zentripetalbeschleunigung, sogar wenn
![]() ist.
ist.
Wir setzen:
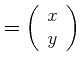 |
(4.149) | |
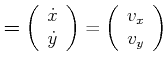 |
(4.150) | |
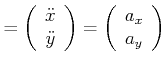 |
(4.151) |
Wegelement:
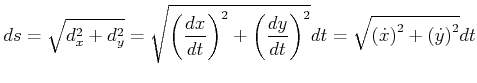 |
(4.152) |
Tangentenvektor:
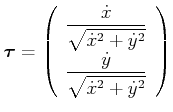 |
(4.153) |
Normalenvektor:
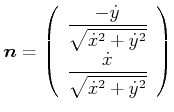 |
(4.154) |
Krümmungsradius:
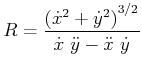 |
(4.155) |
Betrag von ![]() :
:
| (4.156) |
Tangentialbeschleunigung
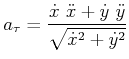 |
(4.157) |
Zentripetalbeschleunigung
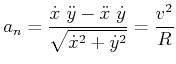 |
(4.158) |
Kontrolle
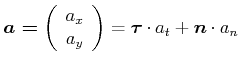 |
(4.159) |
x-Komponente
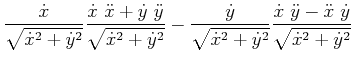 |
||
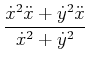 |
(4.160) | |
| (4.161) |
y-Komponente
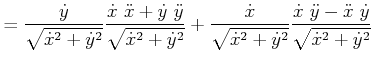 |
(4.162) | |
| (4.163) |
Beispiel:
Schlangenlinie beschleunigt
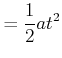 |
(4.164) | ||||||
| (4.165) |
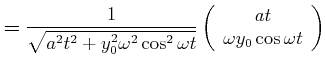 |
(4.166) | |
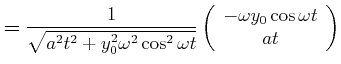 |
(4.167) |
![]() wird mit zunehmendem
wird mit zunehmendem ![]() parallel zur
parallel zur ![]() -Achse,
-Achse, ![]() wird parallel zur
wird parallel zur ![]() -Achse
-Achse
Der Krümmungsradius ist
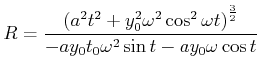 |
(4.168) |
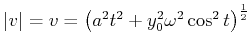 |
(4.169) |
Die Tangentialbeschleunigung (Änderung des Geschwindigkeitsbetrages) ist
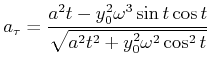 |
(4.170) |
und
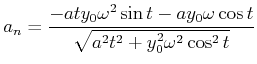 |
(4.171) |
Der Grenzwert wird
Othmar Marti