
Weiter: Dynamik Oben: Mechanik in drei Dimensionen Zurück: Kinematik in drei Dimensionen Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Allgemein gilt
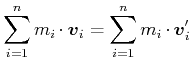 |
(4.173) |
Das heisst:
| In einem abgeschlossenen System ist der Gesamtimpuls eine Erhaltungsgrösse. |
Dabei wird jede Impulskoordinate einzeln erhalten. In kartesischen Koordinatensystemen sind dies die Impulse in
die ![]() -,
-, ![]() - und
- und ![]() -Richtung. In Kugelkoordinaten sind dies die Impulse in der
-Richtung. In Kugelkoordinaten sind dies die Impulse in der ![]() -,
-, ![]() - und
- und
![]() -Richtung. Im Detail besprechen wir die Konsequenzen der Impulserhaltung im Abschnitt 4.4.
-Richtung. Im Detail besprechen wir die Konsequenzen der Impulserhaltung im Abschnitt 4.4.
Allgemein gilt
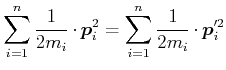 |
(4.175) |
Unter potentieller Energie verstehen wir die Möglichkeit, Arbeit zu leisten, wobei wir die Energie, die in der Bewegung ist, ausklammern. Arbeit im physikalischen Sinne ist
| (4.176) |
Wir betrachten also nur die Komponente der Kraft
![]() , die entlang des Wegelementes
, die entlang des Wegelementes ![]() liegt.
liegt.
Nun ist die Kraft, die das System aufbringt, die Kraft, gegen die wir arbeiten müssen,
![]() . Die im System gespeicherte Energie ist deshalb
. Die im System gespeicherte Energie ist deshalb
| (4.177) |
Damit ist die potentielle Energie definiert durch
|
Einheit der potentiellen Energie :
![]()
|
|
|
|
Definition eines Kraftfelds:
Ein Kraftfeld ist ein Gebiet ![]() , in dem die Kraft
, in dem die Kraft ![]() existiert.
existiert. ![]() hängt dabei eindeutig vom Ort
hängt dabei eindeutig vom Ort ![]() ab.
ab.
| (4.179) |
Beispiel: Gravitation, Magnetfeld, Feder
Kraftfelder können zeitabhängig sein.
Feldlinien
![]() sind Kurven, die in jedem Punkt parallel zu
sind Kurven, die in jedem Punkt parallel zu
![]() sind.
sind.
![\includegraphics[width=0.5\textwidth]{mechanik-031}](img757.gif)
Feldlinien
|
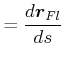 |
(4.180) |
Beispiel Gummiband
Die Länge sei ![]()
Das Feldlinienbild ergibt sich aus
![]()
![\includegraphics[width=0.5\textwidth]{mechanik-032}](img764.gif)
Gummiband als Kraftfeldquelle
|
 |
Definition: Sei
![]() statisch, das Gebiet
statisch, das Gebiet ![]() sei einfach zusammenhängend
sei einfach zusammenhängend
![\includegraphics[width=0.7\textwidth]{mechanik-033}](img767.gif)
Berechnung der potentiellen Energie auf einer geschlossenen Bahn
|
![]() ist konservativ, wenn
ist konservativ, wenn
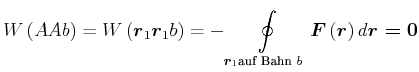 |
(4.181) |
unabhängig von ![]() gleich null ist
gleich null ist
![\includegraphics[scale=0.75]{mechanik-034}](img769.gif)
Unabhängigkeit der potentiellen Energie vom Weg.
|
| (4.182) |
wegen der Tatsache, dass in einem konservativen Kraftfeld die Arbeit auf jedem geschlossenen Weg null ist.
![\includegraphics[scale=0.5]{mechanik-035}](img773.gif)
Wirbelfreiheit konservativer Felder.
|
Ein Kraftfeld ist konservativ, wenn
| (4.183) |
Nach Stokes gilt
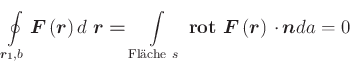 |
(4.184) |
da ![]() beliebig ist und auf einer beliebigen Bahn
beliebig ist und auf einer beliebigen Bahn ![]() das Linienintegral
entlang eines geschlossenen Weges verschwindet, muss
das Linienintegral
entlang eines geschlossenen Weges verschwindet, muss
![]() gelten.
gelten.
Die potentielle Energie ist eindeutig definiert, da in einem konservativen Kraftfeld ![]() unabhängig von
unabhängig von ![]() ist.
ist.
Potentielle Energie und Arbeit der Feldkraft
![]()
![\includegraphics[width=0.7\textwidth]{mechanik-036}](img779.gif)
|
Beweis:
![]() sei bezüglich
sei bezüglich
![]() definiert. Das heisst, dass
definiert. Das heisst, dass
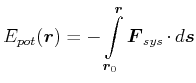
Beispiel: Die Gravitation in Erdnähe wird durch das Kraftgesetz
| (4.187) |
beschrieben.
|
|
Die dazugehörige potentielle Energie ist
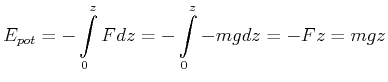 |
(4.188) |
|
|
|
|
Wir betrachten ein System, dessen Energie konstant ist.
| (4.189) |
Dabei ist ![]() die noch unspezifizierte innere Energie eines Teilchens. Für Massenpunkte ist
die noch unspezifizierte innere Energie eines Teilchens. Für Massenpunkte ist
![]() .
.
Die Konstanz der gesamten Energie ![]() bedeutet, dass deren zeitliche Ableitung null sein muss
bedeutet, dass deren zeitliche Ableitung null sein muss
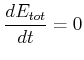 |
(4.190) |
Diese Gleichung ist ein Ausdruck des Hamiltonschen Prinzips, dass die Gesamtenergie konstant sei. Im Einzelnen hat man
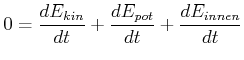 |
(4.191) |
Nehmen wir nun an, dass die innere Energie konstant sei (z.B. Massenpunkte). Dann ist
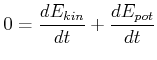 |
(4.192) |
Die Bewegungsgleichung für einen Massenpunkt. Als Beispiel nehmen wir an, dass
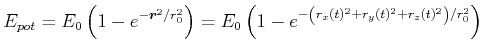
sei. Die kinetische Energie ist entsprechend
![$\displaystyle E_{kin} = \frac{1}{2}m\left(\frac{\partial \vec{r}(t)}{\partial t...
...{\partial t}\right)^2+
\left(\frac{\partial r_z(t)}{\partial t}\right)^2\right]$](img792.gif)
Aus dem Hamiltonschen Prinzip erhält man dann
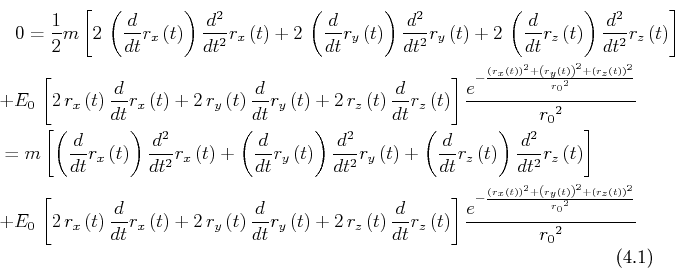
Diese Gleichung kann auch mit Vektoren geschrieben werden. Wir setzen
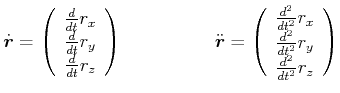
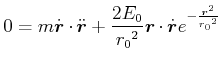
Für
![]() kann die Bewegungsgleichung als
kann die Bewegungsgleichung als
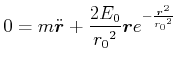 |
(4.193) |
geschrieben werden.
|
|
Beispiel Hebel
|
|
Die Grösse
![]() , also die Arbeit, wird beim Hebel erhalten.
, also die Arbeit, wird beim Hebel erhalten.
| (4.194) | ||
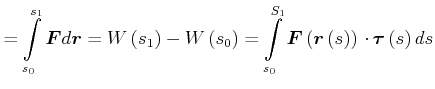 |
(4.195) |
dabei ist ![]() der Weg entlang der Bahn!
der Weg entlang der Bahn!
also
| (4.196) | ||
| (4.197) |
Beispiel:
Kreisbahn
![]()
Beispiel:
Luftwiderstand
dann ist
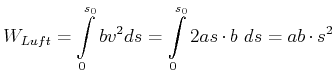
Gleitreibung
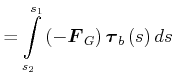 |
||
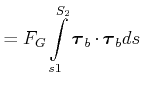 |
||
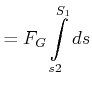 |
||
das heisst, die Arbeit ist, wie erwartet, proportional zur zurückgelegten Strecke.
Bei der Berechnung der Arbeit spielt Zeit keine Rolle. Wenn wir die Zeit, in der eine Arbeit geleistet wird, berücksichtigen wollen, sprechen wir von Leistung. Sie ist durch
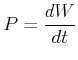 |
(4.198) |
oder
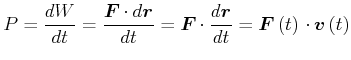 |
(4.199) |
definiert.
Beweis:
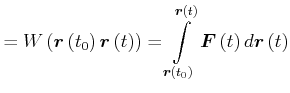 |
||
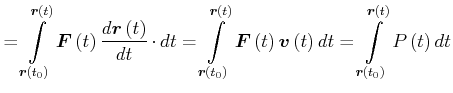 |
(4.200) |
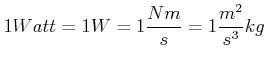 |
(4.201) |
| (4.202) |
Definition des Gradienten:
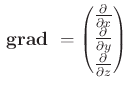 |
(4.203) |
Beweis:
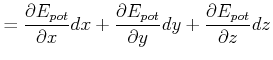 |
||
![$\displaystyle =\left( \begin{array}[c]{c} \frac{\partial E_{pot}}{\partial x}\\...
...\end{array} \right) \left( \begin{array}[c]{c} dx dy dz \end{array} \right)$](img820.gif) |
(4.204) | |
| (4.205) | ||
![$\displaystyle =d\left[ -\int\limits_{\vec{r}_{0}}^{\vec{r}}\vec{F}\left( \vec{r}\right) d\vec{r}\right] \vec{=-F}\left( \vec{r}\right) d\vec{r}$](img822.gif) |
(4.206) |
Othmar Marti