
Weiter: Klassische Relativität beschleunigter Bezugssysteme Oben: Relativität Zurück: Relativität Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Die klassische Relativität beruht auf den folgenden drei Grundlagen:
![\includegraphics[width=0.7\textwidth]{relativ-001}](img1451.gif)
2 Koordinatensysteme
|
![]() heisst Inertialsystem, wenn ein kräftefreier Massepunkt sich gleichförmig bewegt.
heisst Inertialsystem, wenn ein kräftefreier Massepunkt sich gleichförmig bewegt.
|
Relativitätsprinzip
Wenn und ist |
|
|
Für das Folgende setzen wir
![]() . Diese Bedingung kann immer erfüllt werden: wir
müssen nur das Koordinatensystem drehen. Dann haben wir
. Diese Bedingung kann immer erfüllt werden: wir
müssen nur das Koordinatensystem drehen. Dann haben wir
|
|
Die Geschwindigkeiten addieren sich
| (5.422) |
Die Gesetze der klassischen Mechanik sind invariant unter der Galileitransformation
| (5.423) | ||
| (5.424) | ||
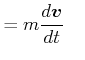 |
(5.425) | |
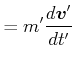 |
(5.426) |
Beweis:
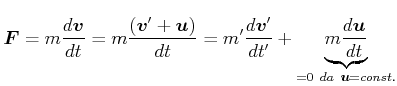 |
(5.427) |
Othmar Marti